[ 3D vision - Study ] - The Pinhole Camera Model and Epipolar Geometry - 1

최근에 3D vision에 관심이 생겨서, 관련 공부를 하고 있었습니다. 해당 포스팅은 Pinhole Camera와 Epipolar Geometry에 관련해서 스터디를 한 내용을 정리하기 위함입니다. 추후에는 Point Cloud Networks와 Nerual Fields(Nerf)에 대해 다루겠습니다. 해당 내용은 Hartley and Zisserman's book의 내용을 참고하였으며, 이광무 교수의 THE RED강의를 수강후 작성하였습니다. 

 

1. Homogeneous Coordinates and 2D Homography

먼저 위의 그림상에서 3D 점과, 선을 나타낼 수 있는 Homogeneous coorodinates에 대해 다룰 것이며, 점들과 선분들이 2차원적인 측면에서 어떤 관계를 이루고 있는가에 대한 2D Homography를 다루도록 하겠습니다.

 

이 후에는 Pinhole Camera라는 실제적인 3D Camera model을 다루고, 그 후에는 6 DoF에 대한 camera parameterazation, epipolar geometry에 대해 다루겠습니다.

 

Homogeneous coordinates

homogeneous coordinates

homogeneous coordinates에서는 scale이 중요하지 않습니다. 우리는 위와같은 선을 line $l = [a, b, c]$라고 하고, point $x= [x, y, 1]$이라고 부르게 됩니다. 그리고 해당 좌표계에서 중요한 특성이 있는데, $l$과 $l'$의 교차점 x는 $l \times l'$과 같이 외적으로 구할 수 있고, $x$와 $x'$을 통하는 line $l$은 $x \times x'$으로 구할 수 있다는 점입니다. 뿐만아니라 고등학교 물리시간에서 배웠겠지만 자기 자신과의 외적값은 0입니다. 이는 이후에도 많이 활용되는 식이므로 숙지하는 것이 좋습니다.

 

간단히 위에서 설명한 식을 계산하는 방법과 기호를 설명하겠습니다.

• $x \times x' = [x]_{x}x'$
• $x = [x, y, z]; $\[ [x]_x = \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{bmatrix} \]

이는 skew-symmetric matrix라고 하며, 이는 벡터와의 외적을 행렬 곱으로 표현할 때 사용됩니다.

 

2D Homography From one image to the other

우리가 위 그림을 볼때, 3D 물체와 2D 그림상의 explicit한 관계를 안타깝게도 설명할 수 없습니다. 그래서 우리는 3D 지점, 2D 지점이 주어졌을때 이 지점들이 어떤 물리적인 설정을 만족하느냐 안 하느냐를 나타내는 implicit한 정의를 내리게 됩니다. 

위와같은 2D -> 2D의 변환을 보게될건데 이를 $H$라는 projective transformation 행렬으로 표현할 수 있습니다. $H$행렬은 9개의 변수를 조작할 수 있지만, scale에 관계없기 때문에 8(=9-1) DoF가 됩니다. 그리고 보다 제한적인 변환들이 sub transformation형태로 존재하게 됩니다. 예를 간단히 들면 2 DoF의 Translation변환, 3 DoF의 Rotation과 Translation변환, scaling까지 추가한 4 DoF 변환이 있습니다. 또다른 예로 Euclidean transformation도 있는데, 이는 SE3변환이라고도 불리우며, 3D에서 물체가 변환될때의 변환을 말합니다. 사실상 SE3변환은 특수한 경우이며 물리적으로 rigid body(강체)가 작아졌다가 커졌다가 할 수 없기 때문에 카메라 상에서는 SE3변환은 사용되지 않습니다.

 

마지막으로 중요한 특성중에 하나가 선형대수시간에 들어봤을 6 DoF의 Affine transformation인데 이는 위에서 설명한 4 DoF의 transformation과 구분을 둘 필요가 있습니다. Affine transformation은 가까워지고 멀어지고가 아니라, 좀 기울여지고 실질적으로 3차원 물체가 일으킬 수 없는 변환도 표현이 되기 시작합니다. 

 

이러한 Homography는 3D 평면 간의 대응을 나타내기 때문에 3D 정보를 복원하거나 모델링하는데에는 많은 한계점이 있습니다. Homography는 두 이미지간의 깊이를 설명하지 못하기 때문에 깊이 정보를 상실한다거나, 같은 평면을 본다고 가정을 해야한다거나,.. 제약이 많습니다. 그래서 실제로 3D 모델링을 하기 위해서는 포스팅의 끝 즈음에서 볼 Fundamental Matrix와 Essential Matrix를 활용해서 이미지 사이의 epipolar geometry를 설명하여, 카메라의 상대적인 위치와 방향을 포함하여 3D 구조를 복원하는데 사용할 수 있습니다.

 

2. Computing the 2D Homography from correspondences

위에서 본 $H$ projective matrix를 내가 카메라로 찍은 이미지로부터 어떻게 구할 수 있느냐에 대해 알아보겠습니다.

 

Finding H via Direct Linear Transformation (DLT)

DLT는 실질적으로 쓰이지 않는 방법입니다. 그 이유는 카메라 상에서의 $x, x'$좌표에 noise가 끼기 때문입니다. 이러한 이유때문에 실제로는 더 robust한 방법으로 구하게 되는데, 이러한 방법을 다루는 이유는 나중에 딥러닝과 결합했을때 Homography를 찾는데 쓰일 수 있기 때문입니다.

 

DLT

결국 $x' = Hx$를 외적을 통해 표현하고 $H$를 3개의 row vector로 쪼개고, 계산하면 linear combination이 되는 3th row를 찾을 수 있게 되는데, 이를 제거하게되면 위와같은 $Ah = 0$의 형태를 만들 수 있습니다. 

 

이제 해당 식의 해를 구해야합니다. $H  = 0$일때는 trivial solution으로 두고, 우리는 scale을 신경쓰지 않는다고 하였으니까 $||h|| = 1$(=homogeneous coordinates)로 가정합니다. 참고로 $H = 0$의 의미는 카메라를 아주 멀리 떨어뜨려 놓은 것과 같은 의미가 됩니다. 우리는 무한대 거리에 있는 카메라를 연관짖는것이 어불성설이기 때문에 관심이 없어서 무시하게되는 것입니다.

 

최종적으로 우리는 SVD를 이용해 해당 식의 Null space를 구하면 됩니다. 

 

그 전에, 우리는 Convex Optimization분야에서 본, KKT condition을 통해 라그랑지안 $L$을 세운다음에, constraints를 추가해 최종적으로 $L$를 미분한 식을 0으로 하게하는 값을 찾으면 됩니다.

 

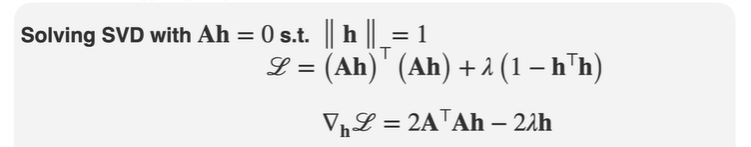
벡터미분을 통해 위와같이 전개해주면 $A^{T}Ah^{*} = \lambda h^{*}$의 꼴이 됩니다. 이는 어떤 matrix를 곱한 h랑 스칼라를 곱한 h가 같다는 문제는 eigen variable문제가 됩니다. 

 

결국 위 식이 최소가 될 때에는 $L(h^{*}) = \lambda$이고, 라그랑지안의 최적의 해 $h^{*}$는 결국 $\lambda$가 가장 작을때입니다. 따라서 $A^{T}A$를 SVD를 통해 가장 작은 eigen value인 $\lambda$와 eigen vector $h$ 를 구하게 되면 우리가 최종적으로 구하고자 하는 Homography를 이때의 eigen vector $h$로서 구할 수 있게 되는 것입니다.

 

DLT does not give the best geometric solution

우리는 이렇게 구한 solution을 Algebric solution이라고 부릅니다. $||Ah|| = ||x' \times Hx||$는 그냥 수식적으로 두개의 식이 같으니까 외적의 값이 0이다라는 수식적으로 표현된 값의 해 입니다. 하지만 우리가 사실 찾고자 하는 값은 이게 아닙니다. 우리가 찾고자 하는 것은 $h$중에 한 이미지에서 다른 이미지로 포인트를 보냈을 경우 원래 가야할 위치로 제일 잘 가는 $h$를 찾고 싶은 것입니다. 이는 $||x' - Hx||$를 minimize해야하는 것이죠.

 

이론상으로 두개의 해가 완전히 충족될 수 있다고 하면 두개가 같은 solution을 가지게 됩니다. 근데 실질적으로 두 이미지 간의 좌표를 연관시킬 때에는 noise가 낄 수 밖에 없고 이럴 때에는 두 개가 다른 해를 가지게 됩니다. 그래서 물리적으로는 맞지 않는 해를 가질 가능성이 높습니다. 하지만 앞서 말했듯이 SVD가 미분 가능한 operation이기 때문에 DN에 넣어주기 딱 좋다는 점을 기억해야합니다.

 

Normalization is Important

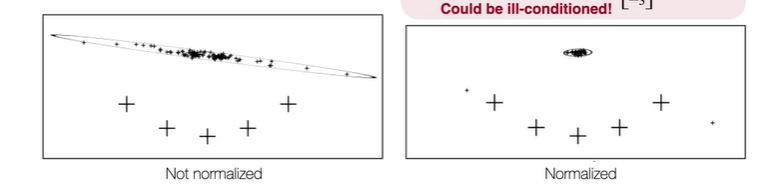
우리가 구하고자 하는 $A$는 Ill-conditioned일 수 있습니다. 그 이유는 $x = [x1, x2, 1]$에서 $x1, x2, 1$간의 크기 차이가 있고, 이를 $x^T$와 내적했을때 값은 천차만별일 수 있기 때문입니다. 즉 우리는 $x1, x2$의 값을 0~1사이의 값으로 normalization해주는 과정이 필수적이라는 점을 알아두어야 합니다.

 

다음 포스팅부터는 Homography로는 설명할 수 없는 3D -> 2D로의 형상변환은 어떻게 이루어지는 가에 대해 자세히 알아보겠습니다.