[ 3D vision - Study ] - The Pinhole Camera Model and Epipolar Geometry - 3

5. Epipolar Geometry and the Fundamental Matrix

이번에는 카메라간의 상관관계를 묘사하는 하나의 수식을 유도할 것입니다. 지금부터의 수식은 지금까지 얘기했던 Camera Calibration이 되어있다고 가정할 것입니다.

 

또한, 3D, 2D상의 선분들을 잇게 되면, 어떤 평면을 구성한다는 것을 알아야 합니다. 여기서 가정을 할 것은 카메라에 맺히는 2개의 대응되는 지점이 어딘지를 안다고 가정할 것입니다. 사실상 이 대응되는 지점을 알아내는 것이 3D vision의 핵심이지만 우리는 이론적인것을 유도하고 있기때문에, 이는 풀어졌다고 가정을 하는 것입니다.

 

이제 우리는 신기한 일을 할 수 있게됩니다. 우리가 3D 어디에서 카메라의 두 선분이 만나는지 몰라도, 두개의 대응점을 통한 하나의 plane을 구성할 수 있습니다. 그리고 이 plane은 항상 두개의 camera를 이은 선분을 지나간다는 중요한 특징을 발견할 수 있습니다. 이 사실을 우리는 수학적으로 모델링을 시작할 것입니다. 모델링이 잘 되어있기만 하다면 3D상에서의 대응점을 찾는 일은 일도 아니게 됩니다.

 

이전에 두개의 대응점이 이루는 plane을 epipolar plane이라고 부르고, 카메라간의 이어진 선분과 이미지 plane상의 교점을 epipole이라고 부릅니다. 그리고 카메라를 이은 선분을 baseline이라고 부르고, epipole과 대응점이 지나가는 선을 epipolar line이라고 부릅니다.

 

Coverging cameras

위 상황은 물체를 안쪽으로 바라보는 camera setting일때, epipolar line이 어떻게 보이는지를 보여주는 그림입니다. 우리는 위와같이 이미지 plane상의 대응점과 epipolar line상의 관계로부터 카메라 관계를 찾아낼 것입니다.

 

이는 카메라가 물체를 평행하게 찍었을때의 상황입니다. 우리는 epipolar line을 그려봄으로서 이미 카메라를 풀기도 전에 점들이 대응이 잘 되는지를 확인할 수가 있습니다. 만약 매칭이 잘 되지 않는다면, camera Calibration이 잘못되었거나 pose estimation이 잘못되었구나를 쉽게 판별할 수 있습니다.

 

A bit more formally

 

3D상의 \( X \) 좌표가 있고, 이는 \( P \)라는 행렬을 통해 이미지 평면상의 \( x \)로 사영(projection)됩니다. 여기서 복잡한 에피폴라(epipolar) 선을 유도하지 않고, 에피폴라 선이 위 상황을 만족하는지 간단히 알아보겠습니다. 점 \( X(\lambda) \)를 다음과 같이 정의합니다: \[ X(\lambda) = P^{+}x + \lambda C, \] 여기서 \( P^{+} \)는 \( P \)의 의사 역행렬(pseudo-inverse)입니다. 이제 이 식에 행렬 \( P \)를 곱해주겠습니다: \[ PX(\lambda) = P \left( P^{+}x + \lambda C \right) = PP^{+}x + \lambda PC. \] 여기서 \( PP^{+} = I \)이고, \( PC = 0 \)이므로 다음이 성립합니다: \[ PX(\lambda) = Ix = x. \] 이 수식은 \( \lambda \) 값과 상관없이 모든 3D상의 좌표 \( X(\lambda) \)가 이미지 평면상의 동일한 점 \( x \)로 사영된다는 것을 의미합니다. 만약 \( \lambda = 0 \)이라면, \( P^{+}x \)는 3D 공간에서 카메라 중심 \( C \)와 해당 선분 사이의 한 점을 나타냅니다. \( \lambda \to \infty \)일 때, 식은 \( C \)로 수렴하게 되어, 이는 카메라 센터로 수렴하는 것을 의미합니다. 따라서, \( X(\lambda) \)는 이 선분 위의 모든 점을 나타내는 식이 됩니다. 이제, 다른 이미지 평면으로 이 점을 사영시켜 봅시다. 이를 \( P' \)를 사용하여 표현하면, 대응되는 점의 좌표는 다음과 같이 됩니다: \[ P'P^{+}x. \] 여기서, \( P'C = C' \)는 이미지 평면상의 에피폴 \( e' \)가 됩니다. 두 점의 외적을 이용해 에피폴라 선 \( I' \)을 유도할 수 있습니다: \[ I' = [e']_{x} (P'P^{+})x = Fx. \] 여기서, \( x \)와 관련 없는 부분을 \( F \)라고 표기하고, 이것을 Fundamental matrix라고 합니다.

 

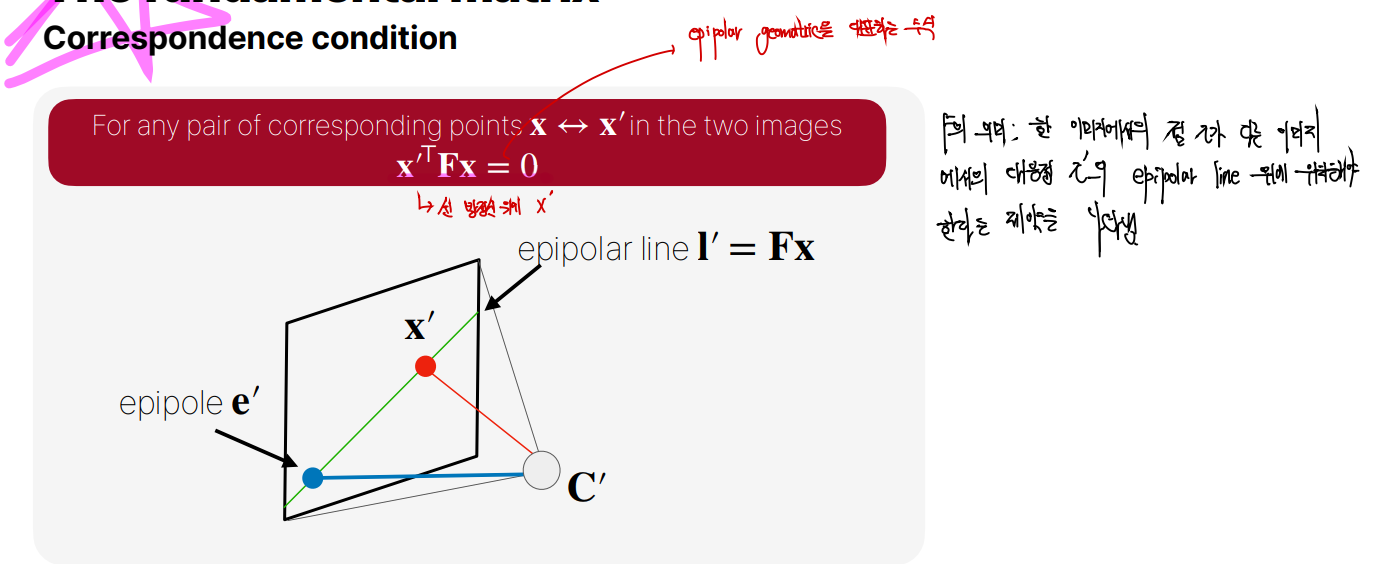
$x'$과 $Fx$를 내적해도 0이므로 $x'^{T}Fx = 0$이라는 수식이 완성되고, 이 관계가 fundamental matrix라 불리는 epipolar geometry를 요약하는 수식이 됩니다. 즉 우리가 두 대응점을 찾게되면, 해당 수식을 무조건 만족해야 한다고 할 수 있겠습니다.

 

몇가지 fundamental matrix에 대한 특징입니다. 그냥 fundamental matrix의 uniqueness와 기하학적 의미와 7 DoF(8 DoF인 Homography보다 제한적임)를 가진다는 특징을 볼 수 있습니다. 

 

6. Computing the Fundamental Matrix from Correspondences

이제 본격적으로 $F$에 대해 어떻게 실질적으로 구하는지를 살펴보겠습니다. 그 전에 몇가지 ambiguity에 대해 다루겠습니다.

 

Projective ambiguity

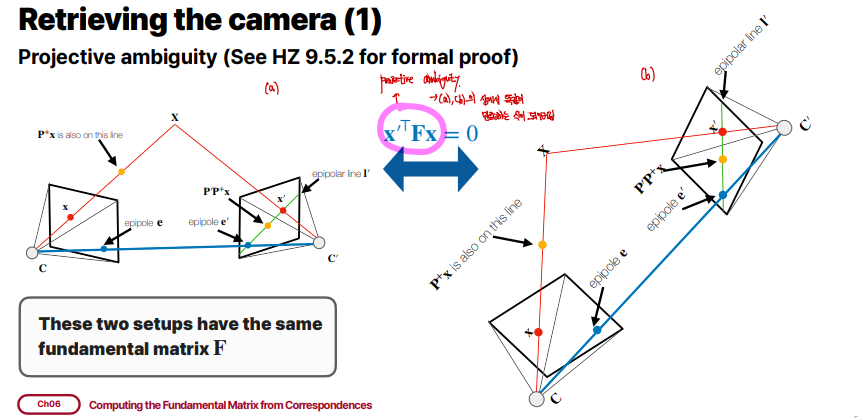
우리가 $x'^{T}Fx = 0$라는 수식이 주어졌을때, 위 두가지 상황은 동일한 상황을 나타내고 있습니다. 위 수식으로서 Projective Ambiguity를 해결할 수는 없습니다. 이 외에도 Similarity Ambiguity가 있는데, 엄청 작은 물체를 보고있는지, 엄청 큰 물체를 카메라가 멀리서 보고있는지 우리는 이 차이를 구별할 수 없습니다.

 

위와같은 ambiguity를 없애주기 위해 일단 우리는 \(P = [I|0], P' = \Big[ [e']_{x}F|e'\Big] \)라고 가정할 수 있습니다. $P$는 아무런 변환을 하지 않는 변환입니다. 이렇게 둔 이유는 하나의 카메라를 어디에 두든 수식적으로 차이가 없습니다. 그래서 우리가 놓기 가장 편한 곳에 둘 수 있는 것입니다. \(P'\)는 먼저 실제 유도된 결과를 놓고 우리가 맞다는걸 증명하기 위해 알려진 사실을 지정한 것입니다.

 

\(F = [e']_{x}(P'P^{+})\)는 Fundamental matrix에서 나왔던 식입니다. 해당 식에다가 \(P, P'\)의 값을 집어넣어주겠습니다. 이때 \(P^{+}\)는 \(P\)가 Identity라고 했으므로 dimension을 맞춰주는 과정을 통해 위와같이 작성할 수 있습니다. 그리고 쭉쭉 수식적으로 전개를 해주게 되면, \(e'^{T}F = 0\)라는 사실을 알고있으므로 이용해서 분배법칙을 해주면, 최종적으로 \[F = \lambda F.\] 라는 수식이 완성됩니다. \(\lambda\)는 임의의 scalar) 이는 homogeneous coordinates이므로 최종적으로 항등식이 되어, 우리가 지정한 \(P와 P'\)이 epipolar geometry를 잘 만족시킨다고 볼 수 있는 것입니다.

 

뿐만 아니라 그림 맨 아래에 일반적인 Canonical representation을 볼 수 있는데, 어떤 scalar와 어떤 vector를 추가해도 결과에는 영향을 미치지 않습니다. 이는 위에서 우리가 보았던 다양한 ambiguity가 수학적으로도 보여지는 것이라고 할 수 있습니다.

 

이전에 우리가 similarity ambiguity를 볼때 calibrated domain에서 본다고 했었는데, 이를 위해 일단 \(K\)는 알고있다 가정합니다. 그리고 양변에 \(K^{-1}\)를 곱해서 \(K^{-1}x = [R|t]x_{world}\)라고 한다면, \(K^{-1}x\)를 새로운 \(x\)좌표라고 본다면 \([R|t]x_{world}\)와 같이 식을 간단히 표현할 수 있습니다. 결국 아까 구한 정답들이 \(R, t\)에 대입되어 구해질 수 있습니다.

 

우리는 여기서 \(K\)가 없는 상황을 가정했는데, 이를 essential matrix 문제라고 부릅니다. \(K\)가 아무거나 될 수 있는 상태를 fundamental matrix 문제라고 부르는 것입니다. 즉 우리가 normalize라고 불리는 x좌표계의 변환을 진행한 상태에서의 문제를 essential matrix 문제라고 부릅니다. 결국 \[E = [t]_{x}R.\]이라는 수식으로 표현되게됩니다.

 

\(r, t\)를 알면 essential matrix를 구하는건 위의 수식을 통해서 구하면 되고, fundamental matrix를 구하고 싶다면 \(K\)만 적용해서 적용시키면 구할 수 있습니다. \(F = K_{2}^{-T}EK_{1}^{-1}, E = K_{2}^{T}FK_1\)

 

우리는 Essential matrix에서 이제 \(R, t\)를 분해하는 걸 해보겠습니다. 먼저 3x3 skew-symmetric matrix S를 우리는 SVD와 같은 형태로 나타낼 수 있는데 \[S = Udiag(1, 1, 0)WU^T.\]입니다. 여기서 \(U\)는 orthogonal matrix인데, \(WU^T\)에서 \(W\)가 permutation matrix이므로 \(WU^T\)또한 orthogonal matrix임을 알 수 있습니다. 이때 \(diag(1, 1, 0)\)이 SVD에서 diagonal term, \(WU^T\)가 SVD에서 \(V^T\) term임을 알 수 있습니다. 이제, Essential matrix를 직접적으로 SVD한 term이랑, Standard form을 SVD한거랑 연관성을 지을 수가 있게 되고, 이를 통해 우리가 모르고 있는 \(W, U\)를 구할 수 있다는 것입니다.

 

\(E = Udiag(1, 1, 0)V^T = SR = Udiag(1, 1, 0)WU^TR\)이됩니다. \(R\)은 rotation matrix라는 것을 알고있습니다. 이 rotation matrix는 \(UXV^T\)로 분해될 수 있습니다. 이는 SVD로 증명이 가능하며, 직관적으로 어떤 회전과 어떤 회전사이의 차이만큼을 곱해주게 되면, 그만큼을 상쇄하는 회전이 되는 원리와 비슷합니다. 이는 rotation이 갖는 특성이 매우 제한적이기 때문에 가능한 것입니다.

 

이렇게까지 표현한 이유는 \(Udiag(1, 1, 0)WU^TUXV^T\)에서 \(U^{T}U\)를 없애주기 위한 것이었습니다. 그럼 최종적으로 \(E = Udiag(1, 1, 0)(WX)V^T\)가 됩니다. 여기서 초기의 식과 같아야하므로, \(WX\)가 Identity가 되어야 하므로 \(X = W\) or \(X = W^T\)여야합니다. 그 이유는 해당 식이 homogeneous coordinates이기 때문에, 부호에 상관없습니다.

 

위에서 본 특성을 이용하면 \(St = [t]_{x}t = 0\)임을 알 수 있습니다. 그 이유는, skew-symmetric matrix의 성질입니다. 이를 통해 \(t = U(0, 0, 1)^T = u_3\)즉 가장 작은 singular vector임을 알 수 있습니다. 간단히 \([t]_{x}t\)을 \(t = U(0, 0, 1)^T\)로 대입해서 실제로 0이 나오는지 확인해보겠습니다. \(Udiag(1, 1, 0)U^{T}U\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = U \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \)이 됩니다. 이 또한 homogeneous coordinates이므로 \(u_3, -u_3\)중에 하나가 됩니다. 즉 \(P'\)는 위 그림에서처럼 4가지 경우가 나오게 됩니다.

 

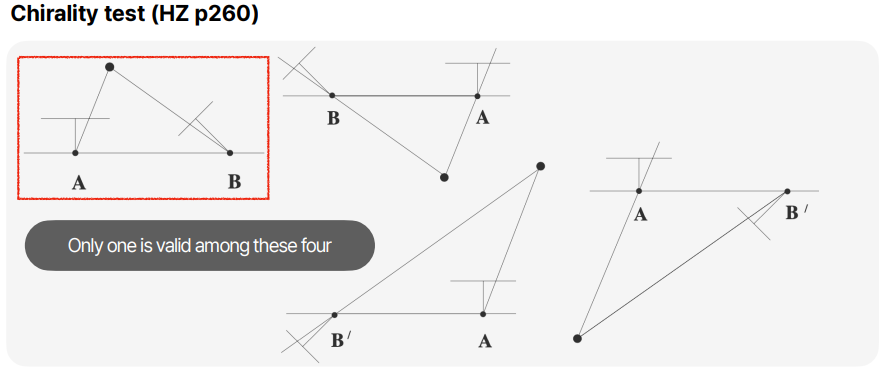
이제 이러한 경우를 직접 그려보면, 물리적으로 말이 안되는 상황이 포함되어있음을 볼 수 있습니다. 이러한 일이 발생하는 이유는, 우리는 물체가 카메라 뒤에있다, 등의 정보를 수식에 주어지지 않았고 오직 선분이 만나는 지점을 고려해서 식을 작성했기 때문입니다.

 

실제로 OpenCV에서 decomposeEssentialMat()의 정의를 보게되면, input으로 Essential Matrix를 보내면 output으로 \(R, t\)를 반환하는 것을 볼 수 있습니다. 또한, chirality test는 수동으로 하게끔 되어있는 것을 볼 수 있습니다.

 

Retriveing the fundamental matrix

이제 fundamental matrix그 자체를 구하는 방법에 대해서 Unnormalized eight-point algorihtm을 통해알아보겠습니다. 해당 알고리즘은 실제로 잘 동작하지 않습니다. 우리는 지금 \(x, x'\)대응점에 노이즈가 없다고 가정하지만, 실제로는 노이즈가 엄청 많을 것이기 때문입니다. \(x'^{T}Fx = 0\)자체를 풀어쓰면 아래와같습니다.

 

위와같이 분해할 수 있게되고, 우리가 모르는 부분인 \(F\)와 우리가 알고있는 대응점인 \(x, x'\)를 \(Af = 0\)과 같이나눌 수 있습니다. 위 그림에서는 \(n\)개의 대응점 pair가 A matrix를 구성합니다. 그럼 A matrix를 구해주고 SVD를 수행해주게 되면, Fundamental matrix를 우리는 구할 수 있게됩니다. 

 

여기서 알고리즘 이름이 Unnormalized인 이유는 우리가 normalize를 해주어야 하기 때문입니다. A matrix는 ill-conditioned matrix가 됩니다. 

 

우리가 위와같이 \(Af = 0\)의 해를 구하게되면, 오른쪽 위의 그림과 같이 epipolar line들이 한점을 지나지 않게 됩니다. 그 말은 즉 \(F\) matrix가 rank2 constraints를 만족해야하는데, 실제로는 노이즈 때문에 그럴일이 없다는 것입니다. 따라서 우리는 \(F\)를 \(F'\)로 대치해야합니다. 이는 \(F\)를 SVD를 수행하여 가장 작은 singular value값을 가지고있는 diagonal term을 0으로 만들어주면 됩니다.

 

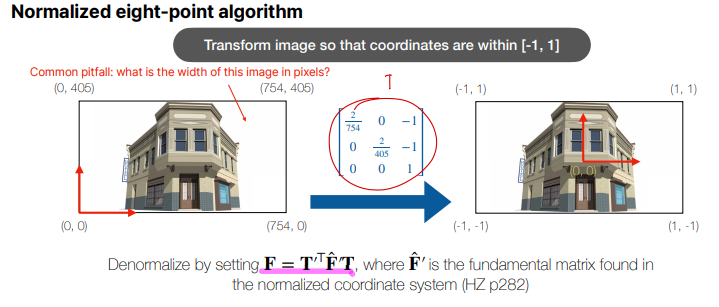
그리고 이미지 좌표를 0~1 사이로 normalize해주어야 하는데, 방법은 위와같습니다. 그냥 Homography 변환해주는 \(T\) matrix를 좌표에 곱해주게 되고 이를 통해 나온 \(\hat{F'}\)를 통해 \(T\) matrix를 활용하여 실제 \(F\) matrix를 \(F = T'^{T}\hat{F}'T\)와 같이 구해주면 됩니다.

 

하지만 위와같이 normalize를 해도 대응점에 노이즈가 끼는 건 방지할 수 없기 때문에 normalize를 한 상태로 노이즈가 최대한 결과에 영향을 미치지 않는 방식으로 robust estimation을 실행하게 됩니다. robust estimation에 대표적인 방법인 RANSAC에 대해 간단히 위의 그림으로 살펴보겠습니다.

 

RANSAC의 주요 아이디어는 무작위 샘플링과 합의(consensus)의 개념을 이용하여 모델을 추정하는 것을 말합니다. 과정은 아래와 같습니다. 대응점을 찾는 알고리즘은 다음 Part인 Point Cloud Network에서 다루며, 여기서는 다 구해져있다고 가정하겠습니다.

1. 무작위로 샘플 선택 
   1. 전체 데이터 중에서 최소한의 점들(모델을 추정하는 데 필요한 최소 개수를 무작위로 선택합니다.)
2. 모델 추정
   1. 선택된 점들로부터 모델을 추정합니다. (Fundamental matrix or Essential matrix)
3. 합의 집합(consensus set)평가
   1. 추정된 모델에 대해 전체 데이터 중에서 이 모델에 잘 맞는 점들을 찾습니다. 이때, 모델에 충분히 가까운 점들은 인라이어(inliner)로 간주하고, 그렇지 않은 점들은 아웃라이어(outlier)로 간주합니다.
4. 모델 최적화
   1. 인라이어의 수가 현재까지 발견된 최적의 모델보다 많으면, 해당 모델을 현재의 최적 모델로 갱신합니다.
5. 반복
   1. 이 과정을 사전 정의된 loop만큼 반복하여, 가장 많은 인라이어를 포함하는 모델을 최종적으로 선택합니다.

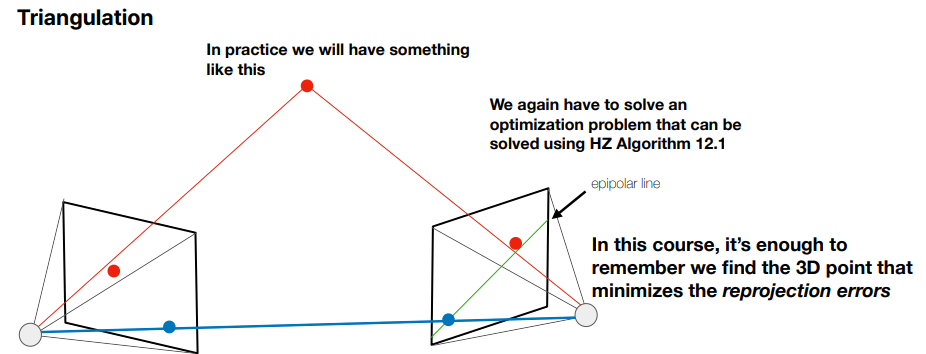
우리는 여태까지 카메라 위치를 찾는 방법에 대해 배웠는데, 3D point를 찾아내는 방법도 있습니다. 이에 대해서는 Part3에서 다루며, 간단히 방법만 서술하자면 대응점에 가장 가깝게 projection되는 3D 좌표를 찾아내는 것으로 3D 복원을 수행하게됩니다.