![[ 3D vision - Study ] - Point Cloud Networks (Finding Good Correspondeces) - 1](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FLsyLh%2FbtsJUbwqqAb%2FFOmd3ZrEEm7ObKny8BA291%2Fimg.png)
이전에는 good correspondences를 잘 찾았다고 가정하에 수식을 전개했었습니다. 이번에는 good correspondences를 찾기 위해 Camera Pose Estimation Pipeline, Point Cloud Network, Graph Neural Network를 보고, 최종적으로 Correspondences를 학습하는 방법에 대해 보겠습니다.
1. A Typical Camera Pose Estimation Pipeline
위사진은 colmap이라는 software의 pipeline입니다. 간단한 과정에 대해 살펴보겠습니다.
- Feature Extraction
- 이미지들이 주어졌을 때 먼저 Shift / Lift같은 이미지를 설명할 수 있는 local feature들을 추출합니다.
위 그림과 같이 다른 이미지가 주어졌더라도, 특징적으로 볼 수 있는 점들을 알고리즘이 추출해줘서 모든 픽셀을 비교할 필요가 없게끔 하는 것이 이 과정의 목적입니다.
- Matching
- 특징점을 매칭시켜봅니다. 전통적으로는 특징점들마다 discriptor라고 불리는 로컬 정보를 추출해서 서로 비교함으로써 가장 가까운 특징점과 대응시킵니다.
- Geometric Verification
- 이전에 배웠던 Fundamental Matrix같은게 epipolar line을 통해 얼마나 대응이 되는가 안 되는가에 대한 부분입니다. 만약 대응이 되지 않는다면 필터링을 하여서 고려하지 않습니다.
위 그림과 같이 빨간선이 잘못 대응된 선 입니다. 앞으로 우리가 주로 다룰 내용이 geometric verification을 얼마나 잘할 수 있는지에 대한 것입니다.
이 모든 과정을 거친 후에, 이전에 배웠던 Epipolar Geometry를 통해 카메라들을 연결시킨 다음에 Incremental Reconstruction이라는 부분을 만듭니다. 해당 부분은, incremental하게 카메라를 이어 붙히는 방법인데, 이는 자세히 다루지 않겠습니다.
재밌는점이 있습니다. Feature Extraction ~ Matching부분은 2004년 부터 20년간 꾸준히 연구가 되었던 걸 비하면, Geometric Verification부분은 상대적으로 많이 이루어지지 않습니다. 그 이유는 해당 과정을 수행하기 위해 요구되는 Deep Network의 특징에 기인한다고 볼 수 있습니다. 여기서는 대응점(Point)를 다루기 때문에 Point Cloud를 다루는 Deep Network를 사용해야합니다. 나중에 다루겠지만 이는 Permutation equivalent해야하기 때문에 PointNet이 등장하기 전까지는 연구가 활발하지 않았던 것입니다.
2. Processing Point Cloud
위와같이 Point Cloud를 처음으로 다루었던 PointNet [Qi et al., 2017]은 위와같이 CLS, Part Seg, Semantic Seg등을 수행할 수 있습니다. PointNet은 Permutation equivalent하는 방식을 모델에 학습을 시키는게 아니라, 그 구조로서 처리하는 방식에 집어넣습니다. 즉, 각각의 correspondences를 독립적으로 처리하고, 처리한 것들을 최종적으로 한 번에 취합해서 결과를 분석하겠다는 것이 PointNet의 main idea입니다.
PointNet [Qi et al., 2017]
- mlp, max pool
- mlp는 각각의 sequence를 공유되는 mlp(64, 64)를 이용하여, 처리합니다. 최종적으로 max pool을 통해 global feature를 추출합니다.
- input transform, feature transform
- 이전에 배웠던 선형변환(Euclidean transformation)들을 여기서 수행을 하게 됩니다.
- input transform
- 입력된 point cloud를 적절히 변환하여 invariance를 확보합니다. 3d point cloud는 rotation, translation, scaling과 같은 변환에 영향을 받기 때문입니다. 이는 point cloud들이 물체에 관한것이고 그 물체들이 강체 변화 수준의 변화밖에 없다는 것을 알기 때문에 쓸 수 있는 부분입니다.
만약 충분히 많은 h(변환들)을 갖고 있다면 이는 어떤 함수든 간에 표현할 수 있습니다. 저자는 이러한 universal approximation을 PointNet에 넣어서, 모델이 잘 돌아간다는 것을 증명하였습니다. 하지만 이는 실제로 잘 돌아가지 않습니다. 그 이유는 여러가지일 텐데, 이를 해결한 advanced model을 뒤에서 다루겠습니다.
추가적으로 3d에서 많이 다루는 Housdorff distance \(d_H(.,.)\)를 보겠습니다. \(X, Y\)가 각각 어떤 포인트 세트라고 할 때, Housdorff distance를 구합니다. 위에 그림에서 \(X, Y\)로 대응되는 점들이 쭉 있다고 합시다. Housdorff distance는 X의 입장에서 가장 가까운 Y의 점을 찾습니다. 그리고 Y의 입장에서도 찾습니다. (이것이 inf(infimum)연산자가 하는 역할입니다)
다 했다면, X입장에서 찾았을때 가장 큰 distance를 가진 점과 Y입장에서 찾았을때의 큰 distance를 가진 점 중에 더 큰 distance를 Housdorff distance라고 합니다. 더 생각해보면, Housdorff distance가 최소화가 된다면 \(X, Y\) set이 서로 일치하게 될 것입니다. 실제로 두개의 point cloud의 거리를 측정하는 지표가 Housdorff distance가 됩니다.
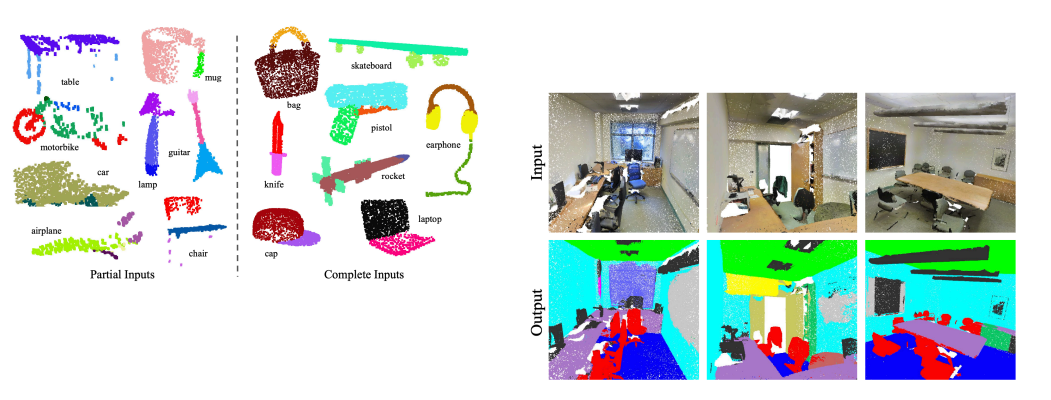
실제로 PointNet은 Part Segmentation과 ScanNet이라는 dataset에서의 Semantic Segmentation이 모두 잘 동작하는 것을 볼 수 있습니다.
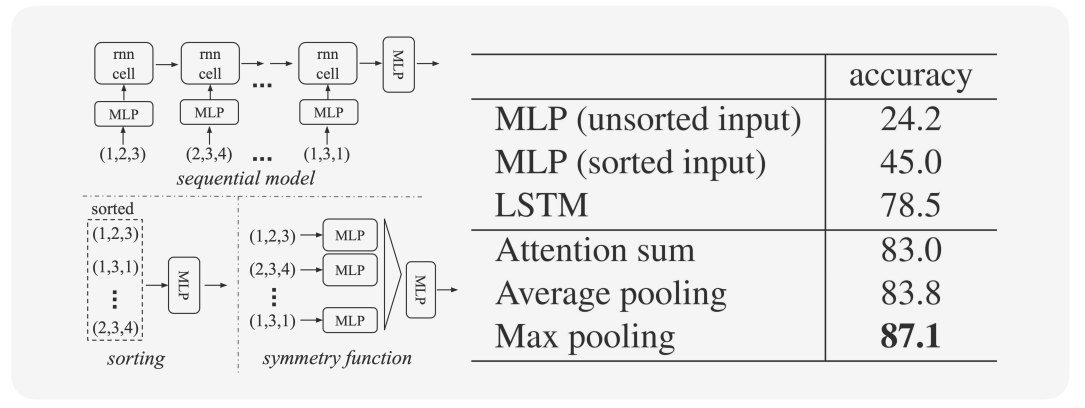
또한, correspondecne가 들어올 때 나한테 어떤 하나의 월드가 들어온 것으로 생각하고 언어 모델도 생각하고 풀 수 있습니다. 이런경우 모델의 성능은 위와 같습니다. PointNet과 같이 permutation equvalent을 architecture적으로 푼 모델이 기존 다른 모델보다 성능이 높게 올라간 걸 볼 수 있습니다.
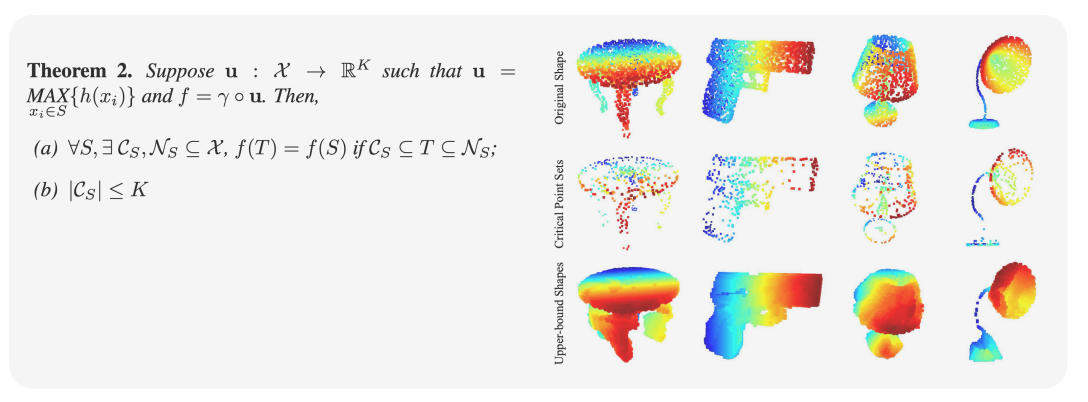
PointNet 자체가 최댓값 (max score)를 통해 결과를 도출합니다. 즉 indivisual한 각각의 point들이 어떤 영향을 미치는 가 도 살펴볼 수 있습니다. 위 그림에서는 점들을 빼고 추가했을때 original 물체의 종류를 인식할 수 있는지에 관련된 것입니다. Critical Point Sets를 보면, 어느정도 PointNet이 물체의 틀을 이해하고 있다고 볼 수 있습니다. 이는 즉, Neural Network이 물체의 개념을 배웠다고 볼 수도 있는 것입니다.
PointNet++ [Qi et al., 2017]
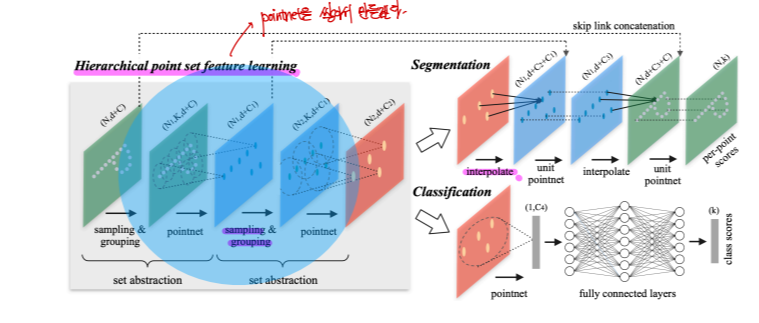
기존의 PointNet에는 계층구조가 없습니다. 이를 보완하기 위해 PointNet저자가 PointNet++를 만들었습니다. 이는 sampling & grouping, pointnet, interpolation등으로 이루어져있습니다. 이들은 point cloud에 locality를 추가하기 위해 사용되는 기법들이며 아래에서 디테일을 살펴보겠습니다.
샘플링은 전체 point cloud에서 균등하게 분포된 대표 포인트들을 샘플링하는 과정입니다. 이 단계에서 Farthest Point Sampling(FPS)가 사용되어 point cloud를 균등하게 줄이게 됩니다. FPS는 하나의 포인트로부터 순차적으로 가장 멀리 떨어져있는 지점을 선택해서 coverage(=maximize spreadness)를 높일 수 있는 방법입니다.
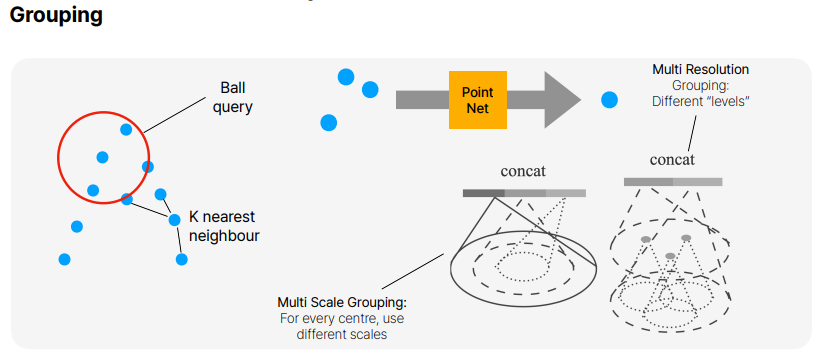
그룹핑은, Ball query나 K-NN방식을 사용하여 주변의 point cloud를 묶는 작업입니다. 이 묶여진 point cloud는 우리가 잘 알고있는 PointNet의 input이 됩니다. 여기서 그룹핑을 할때에는 sampling이전의 point cloud set에서 그룹핑이 되어집니다.
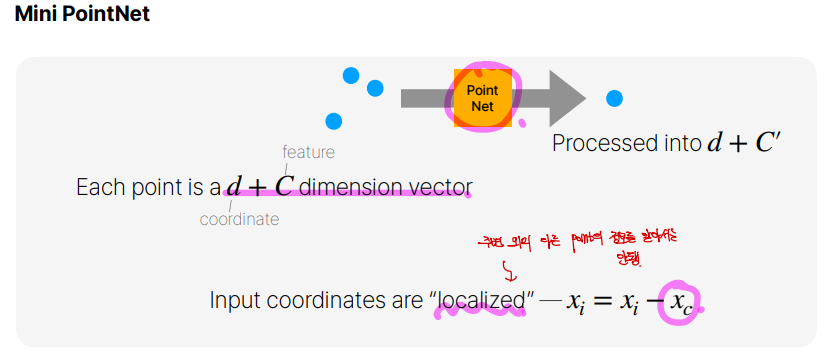
PointNet에 넣기전에 우리는 localization을 해줍니다. 그 이유는, PointNet에 넣어지는 input은 자기들을 제외한 point cloud의 위치를 알아서는 안됩니다. 그래서 point cloud의 중심을 빼주어서 point cloud의 중심을 0으로 만드는 작업을 해주는 것입니다.
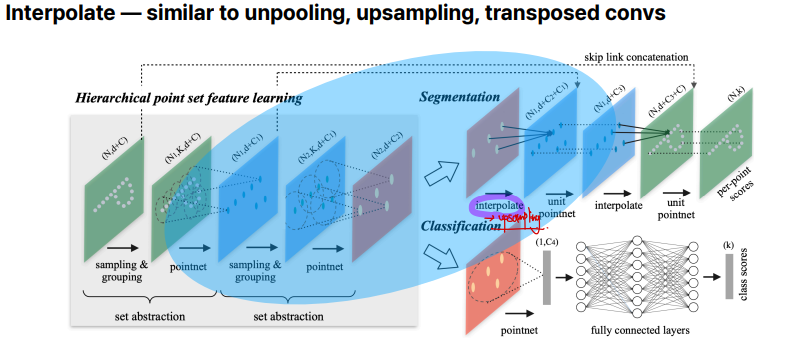
Interpolate는 Segmentation을 할 때만 사용됩니다. 이는 CNN에서 upsampling이라고 볼 수 있습니다. 몇개없는 sample로부터 interpolation을 통해 원래의 point cloud의 개수만큼 만들어주는 것입니다.
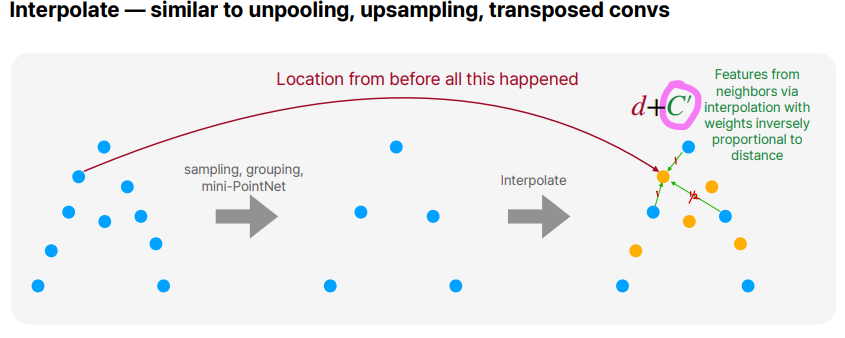
위의 그림에서는 거리에 반비례해서 가중치를 주어 interpolation하는 과정을 볼 수 있습니다.
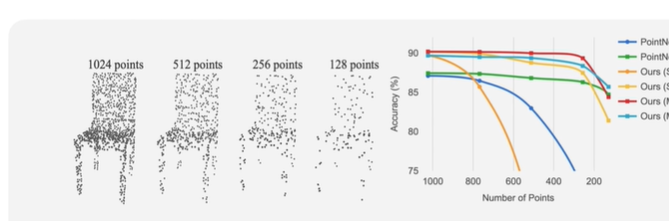
위에는 ModelNet 40(3D Cad)와 관련된 dataset을 통해 PointNet과 PointNet++를 비교한 실험결과 입니다. 또한, DP라는 기술이 적용되었느냐 적용 되지 않았느냐도 중요한데, DP는 data agumentation이 적용되어 sparse한 point cloud에서도 더 잘 동작하게 하는 기술입니다.
예를 들어 파란색 선을보면, 이는 PointNet에 DP가 적용되지 않았고 초록색 점을보면 DP가 적용되었습니다. DP가 적용되지 않은 파란색 선은 128point에서 잘 동작하지 않는 것을 볼 수있습니다. 그리고 PointNet++는 DP가 적용되지 않는 것도, Accuracy가 잘 떨어지지 않는 것을 볼 수 있습니다. 이는, PointNet++에 적용된 locality가 sparsity에 robustness하다는 것도 알 수 있습니다.
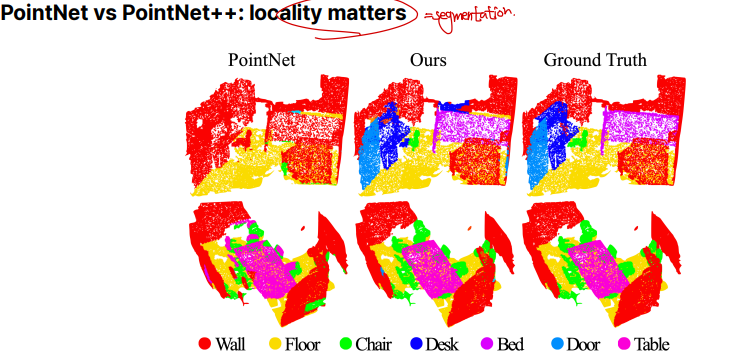
Instance Segmentation에서는 locality의 중요성이 더 부각됩니다. PointNet과 PointNet++을 비교했을때 locality를 고려한 PointNet++가 더 잘 되는 것을 볼 수 있습니다.
PointConv [Wu et al., 2019]
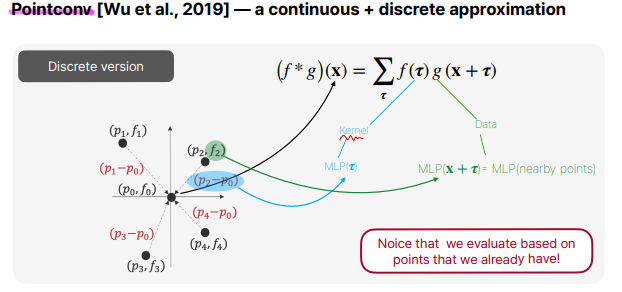
PointConv는 실제로 convolution연산을 point cloud에 적용한 논문입니다. 위 그림을 보면, center point cloud로부터의 K개의 이웃을 구한다음에 \(p_n - p_m = \delta\)을 통해 relative distance를 구하고, 각각의 relative distance마다 다른 kernel함수 \(f_n\)을 통해 위와같이 discrete convolution연산을 정의합니다.
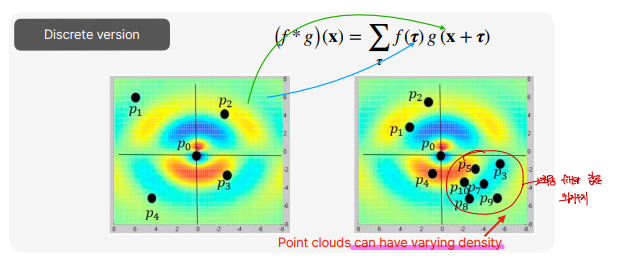
point cloud의 특징을 생각해보면, 종종 한쪽으로 몰려있을 수 있다는 것입니다. 그래서 density가 항상 달라져서, 몇개의 point cloud는 최종 결과에 영향을 못주고, density가 높은쪽의 point들만 영향을 줄 수 있을 겁니다.
이를 해결하기 위해 KDE(kernel density estimation)을 통해 point cloud의 density를 구하고, 이에 inverse proportion의 \(s(\delta)\)를 추가해줌으로써 해결해줍니다.
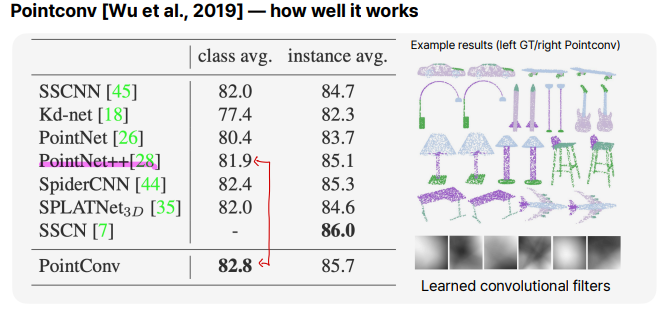
결과를 보면, PointConv가 PointNet, PointNet++보다 결과가 아주 조금 좋습니다. 수학적으로 PointConv의 convolution연산을 추가하는 것이 이전보다 훨씬 좋았지만, 결과적으로는 별로 차이가 나지 않는 것을 볼 수 있습니다.
KPConv [Thomas et al., 2019]
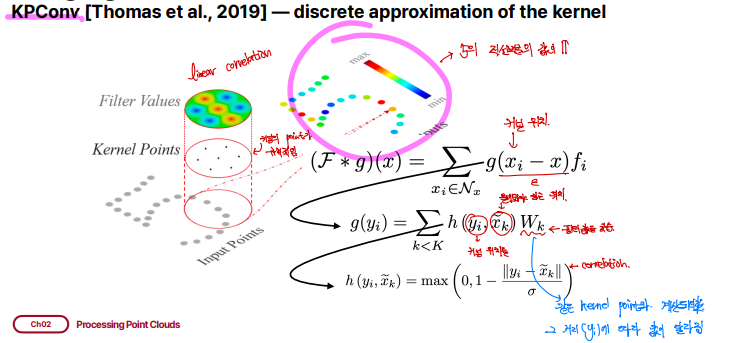
KPConv는 정해진 격자 kernel이 아닌 일정한 반지름 r을 가지는 구 형태의 kernel을 가집니다. 구 형태의 kernel안에는 PointConv에서 convolution kernel grid역할을 하는 kernel point가 있어 이를 이용해 convolution을 수행합니다. KNN을 사용할 수도 있는데, 정해진 r값을 이용하는 것이 point의 density에 robustness하고, 일정한 구 형태의 domain이 network가 의미있는 representation을 학습하는데 도움이 된다고 말합니다.
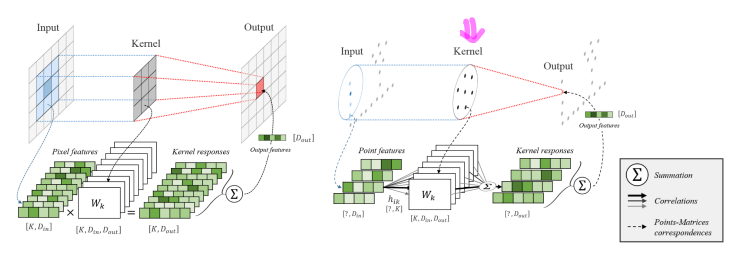
그리고 이웃 포인트들과 커널 포인트 간의 거리를 기반으로 가우시안 함수를 적용하여 가중치를 계산합니다. \(h(y_i, x_k)\)는 포인트 간의 거리가 가까울 수록 큰 가중치를 부여하고, 거리가 멀수록 작은 가중치를 부여하는 방식으로 동작합니다. 이웃 포인트들과의 결과들이 합산되어 중심 포인트의 새로운 특징을 계산하게 됩니다. KPConv는 각 중심 포인트의 새로운 특징 벡터를 생성하게 되는 것입니다.
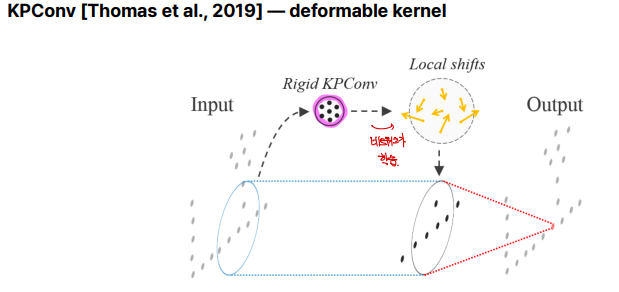
deformable kernel은 고정된 형태의 커널을 사용하는 기존 컨볼루션과 달리, 입력 데이터의 특성에 맞게 커널의 위치나 모양을 동적으로 조정할 수 있는 방식입니다. 이는 복잡한 패턴이나 변형된 구조를 더 잘 학습하기 위해 개발되었습니다.
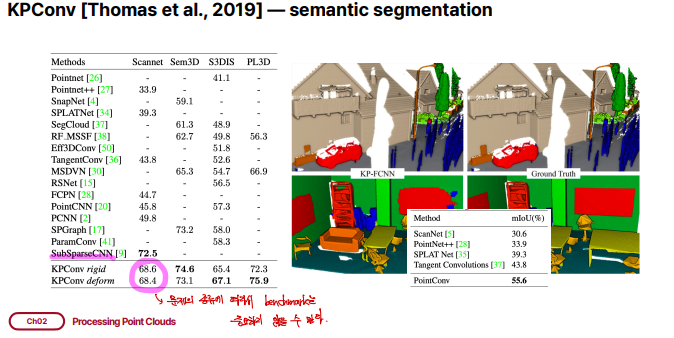
KPConv(rigid, deform)의 결과는 앞에서 본 네트워크보다 좋습니다. 다만, SubSparseCNN과 같은 네트워크보다는 성능이 좋지 않은데, 이는 3d point cloud data를 voxelization을 통해 처리하는 네트워크입니다. 하지만 우리의 목표는 3d vision에서 correspondence를 처리해야하는데, 이는 4d 정보이기 때문에 이를 사용할 수 없습니다.