[ 딥러닝 논문 리뷰 - PRML Lab ] - Score-Based Generative Models and Diffusion Models

DDPM, DDIM의 논문을 읽고 리뷰를 했습니다. 그 후에 Diffusion Models Beat GANs on Image Synthesis라는 논문을 리뷰하려고 읽고 있었습니다. 그런데, diffusion에 class guidance를 도입하면서, 학습시에서의 score matching 어쩌고, 샘플링시에 Annealed Langevin dynamics를 이용한는 내용이 너무 많아서 궁금해졌습니다. 그러면서, DDPM, DDIM그 이전에 나온 Score-Based모델과 같은 NCSN과 같은 모델이 있는걸 알 수 있었고, NCSN이 DDPM과 SDE를 통해 통합될 수 있는 논문등이 있음을 확인할 수 있었습니다. 그럼 이번 포스팅을 통해 DDPM이전의 논의되었던 사항들과 개념들에 대해 간단히 짚고가겠습니다.

NCSN으로 생성한 이미지들

Score-based Generative Models

오늘 다룰 내용의 핵심적인 논문(Generative Modeling by Estimating Gradients of the Data Distribution, NIPS 2019, Song et.al.,)입니다. 해당 내용과 고려대학교 DMQA 랩실 세미나 자료를 참고하였습니다.

 

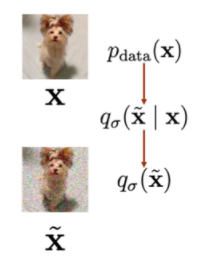
우선 Generative Model을 설명하기에 앞서, 우리는 어떤 이미지들 샘플들의 모집단을 오른쪽과 같은 확률분포로 나타낼 수 있습니다. 이는 다항 혼합 분포 형태로 되어있을것이며, 확률이 높은 곳은 그럴듯한 샘플을 말하는 것이고, 확률이 낮은 부분은 아마 샘플과 전혀 다른 아무 의미없는 노이즈를 말하는 것일겁니다.

 

위와같이 확률밀도함수의 기울기를 계산 후 확률 값이 높아지는 방향으로 데이터를 업데이트 합니다. 이렇게 되면 확률값이 높은 곳에 도달하면 샘플링된 데이터와 유사한 데이터를 생성할 수 있게 되는 것입니다.

 

이제 Score함수에 대해 다루겠습니다. Score란 확률밀도함수의 미분을 말합니다. 즉, 입력 데이터 x에 대한 미분이라고 할 수 있습니다.

$$score = \bigtriangledown_{x}log{p(x)}$$

 

위는 Multivariate Normal Distribution의 예시를 든 것입니다. $p(x)$를 x에 대해 미분한 값을 볼 수 있고, 이를 실제 평균 벡터, 공분산 행렬에 대해 직접 계산한 값을 오른쪽에서 볼 수 있습니다.

 

우리는 실제 데이터의 분포를 모르지만, Score의 값만 알면 데이터를 생성해낼 수 있습니다. 그 이유는 위 그림과 같습니다. Score-Based Generative Model의 과정은 위와같습니다. 먼저 실제 모집단의 데이터로부터 Score(vector field)를 추정합니다. 그 후, 추정된 Score를 바탕으로 새로운 데이터를 sampling합니다. 우리는 전자에서 Score-matching를 사용하며, 후자에서는 Langevin dynamic를 사용하게 됩니다.

 

Score matching

이제 위에서 Score-matching과정을 어떻게 하는지 보겠습니다. 이를 가능하게 하기 위해, 데이터 x에 대해 score값을 계산해주는 모델인 Score Network를 만듭니다. 

 

그래서 우리는 Score Network를 True score(GT)와 맞추어주는 Loss function을 만듭니다. 하지만 우리는 $p(x)$인 실제 데이터 분포를 알지 못합니다. 이를 가능하게 하는 것이, 2005년에 제안되었으며 해당 블로그에 설명이 잘 되어있으니 참고하시기 바랍니다. 이는 복잡한 적분식을 전개하고 부분적분으로 치환하며, $p(x)$가 $x$에서 무한대로 갈 수록 0으로 수렴한다는 가정하에, 항들을 날려버리면서, 위 그림에서 2번째 줄의 식처럼 간단히 변환됩니다.

 

하지만 $tr(\bigtriangledown_{x}^{2}s_{\theta}(x))$를 보면(그림 식이 잘못되었음), $s_{\theta}(x)$인 score값을 2번 미분한 형태입니다. 이는 Jacobian Matrix형태이며, score network의 입력인 $x$의 차원이 $d$라면 $d * d$의 계산 복잡도를 가집니다. 그래서 차원이 증가하면 해당 loss식의 계산 복잡도는 지수적으로 증가하게 됩니다.

 

그리고 최종적으로, 2011년에 Denoising Score Matching이 제안되었으며, 해당 식이 score-matching generative model에서의 최종 objective function이 됩니다(논문에서는 Sliced score matching까지 소개하지만 NCSN의 목적과 더 부합한 denoising score matching을 최종 목적함수로 선택합니다).

 

Denoising Score matching

denoising score matching에서 $q(\tilde{x}|x)$는 데이터 $x$에 조건화된 노이즈가 추가된 데이터 $\tilde{x}$의 조건부 확률 분포를 나타냅니다. 이의 목적은 $\tilde{x}$에 대해 가능한 한 정확하게 원래 데이터 $x$의 위치를 추정하는 것입니다. 여기서 노이즈가 충분히 작으면 원래 데이터의 score를 예측할 수 있습니다. 이를 설명한 것이 위의 맨 마지막 수식에 나타나있습니다. 노이즈가 충분히 작다면, $s_{\theta^*}(x) = \bigtriangledown_{x}log_{q_{\sigma}}(x)$가 성립하고, 이가 $\bigtriangledown_{x}log{p_{data}}$와 근사된다고 논문에서 설명하고 있습니다. 

 

Sliced score matching

Sliced Score matching은 특히 고차원 데이터에서의 계산 복잡성을 감소시키기 위해 개발된 고급 Score matching방법론입니다. 고차원에서 score를 직접 계산하는 대신, 여러  slices로 분할하여 각각의 1차원 투영에서  score를 계산합니다.

 

Score Network

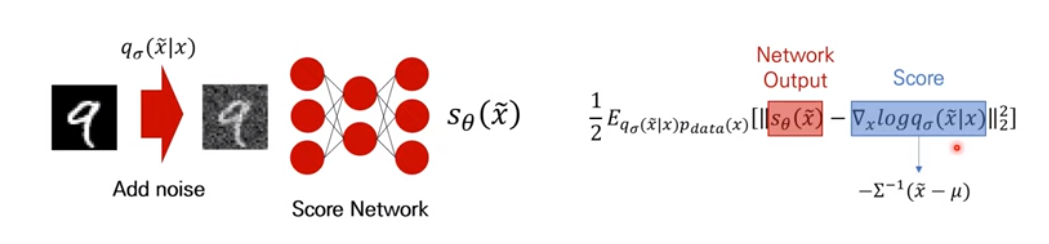
Score Network의 입력값은 실제 샘플 이미지에 노이즈를 씌운 $\tilde{x}$가 됩니다. 그리고 출력값은 해당 데이터의 Score가 될 것입니다. 우리는 해당 과정을 모델링하기 위해 위와같이 Loss식을 세운 것이니까요.

 

이에 목적함수의 $s_{\theta}(\tilde{x})$는 Score Network의 출력값일 것이고, $\bigtriangledown_{x}log{q_{\sigma}(\tilde{x}|x)}$이 부분은 Score값이 될 것입니다. 그리고 이렇게 $q_{\sigma}(\tilde{x}|x)$를 가우시안 노이즈($\tilde{x} = x + \epsilon, \epsilon \sim N(\tilde{x}|x, \sigma^{2}I))$로 가정한다면, 이의 $\tilde{x}$에 대한 미분값은 $-\sum^{-1}(\tilde{x} - \mu)$와 같이 Score값이 계산 될 것입니다. 추가적으로 Score Network은 $\mathbb{R}^d \rightarrow \mathbb{R}^d$차원으로 input, output의 차원은 같습니다. 논문에서는 이러한 Score Network의 특성때문에, 입력차원과 결과차원이 같은 U-net구조를 사용합니다.

 

Langevin Dynamics

Langevin dynamics는 MCMC의 일종으로서 pdf인 $p(x)$로 부터 $\bigtriangledown_{x}log{p(x)}$를 통해 sample을 생성해낼 수 있습니다. 여기서 Lnagevin Dynamics는 연속 확률 미분 방정식을 아래와 같이 사용하게됩니다.

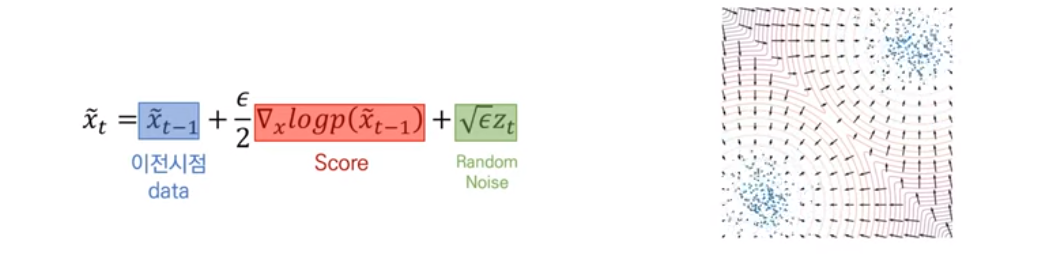
우리가 Score Network를 잘 학습시켰다면, 모든 데이터의 공간상에서 Score를 계산할 수 있습니다. 이를 바탕으로 임의의 데이터인 랜덤 노이즈($\tilde{x_0} \sim \phi(x), \phi = prior distribution$)로부터 시작하여, Score값을 따라 가다보면 실제 데이터(샘플링 데이터)와 근사한 샘플을 뽑을 수 있게 될 것입니다. 이 때, $\epsilon \rightarrow 0$ and $T \rightarrow \inf$라면 $\tilde{x}_T$는 $p(x)$의 exact distribution을 근사한다고 논문에서 설명합니다. 원래는 Metropolis-Hastings으로 위의식의 error를 검증해서 값을 update해나가야 하지만, 이는 $\epsilon is small$ and $T is large$일 때 무시할만 하다고 합니다.

 

Langevin Dynamics의 식을 보면, 이전시점의 data, rescaling된 Score값, Random Noise로 구성되어있는 것을 볼 수 있습니다. 여기서 Random Noise는 Gradient Descent에서와 같이 해당 샘플링 과정이 Local Minimum에 빠지는것을 어느정도 방지하기 위해 넣은 항이라고 볼 수 있습니다.

 

Problem in Low Density Regions (Inaccurate score estimation)

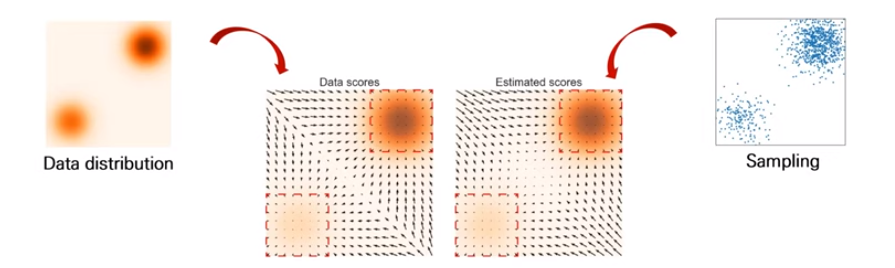
기존에 Score Network를 통해 Score값을 모든 데이터의 차원에서 구했는데, 문제점은 확률값이 낮은 공간에서 학습 샘플이 부족해서 Score의 정보가 부정확하다는 것입니다. 그래서 위 그림을 보면 Estimated Scores와 실제 Data Scores가 차이가 있는 것을 볼 수 있습니다. 위 그림은 $p_{data} = \frac{1}{5}N((-5, -5), I) + \frac{4}{5}N((5, 5, ), I)$에 대한 혼합분포를 나타낸 것인데, score-estimation이 data density가 높은 곳의 근처에서만 reliable한 것을 설명합니다.

 

사실 이는 논문에서 The manifold hypothesis를 설명하면서 Score-matching알고리즘이 low-dimension manifold에서 발생하는 문제점을 상세히 서술하고 있습니다.

• 정의역의 제한: 저차원 매니폴드에 데이터가 한정될 경우, 고차원 주변 공간에서 그라디언트인 스코어 $\bigtriangledown_{x}log_{p_{data}}(x)$는 정의되지 않습니다.
• 일관성의 부재: 만약 Score-matching이 저차원 매니폴드만을 고려하여 이루어진다면, 전체 데이터 공간에 대한 밀도 추정이 아니라 매니폴드 내에서의 로컬 밀도 추정에 집중하게 됩니다.

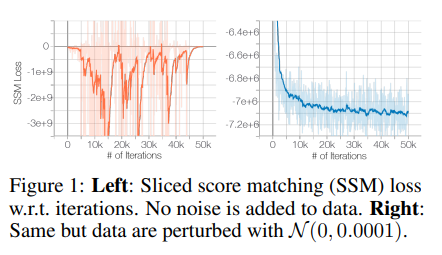
실제 논문에서는, Figure1과 같이 Sliced score matching(SSM)을 ResNet을 사용해서 훈련시킬 때, SSM Loss가 처음에는 줄어들지만 그 이후로는 불규칙하게 진동합니다. 이에 반해 가우시안 노이즈를 추가한 perturb data를 통해 학습을 하면 SSM Loss가 수렴하는 것을 볼 수 있습니다 (이것이 아래에서 볼 해결방안이 됨).

 

Noise Conditional Score Networks

그래서 논문의 저자들은 데이터에 노이즈를 추가한 후 Score값을 추정하자고 합니다. 노이즈가 추가된 데이터가 확률값이 낮은 공간을 채워서 Score의 추정을 가능하게 하기 때문입니다.

 

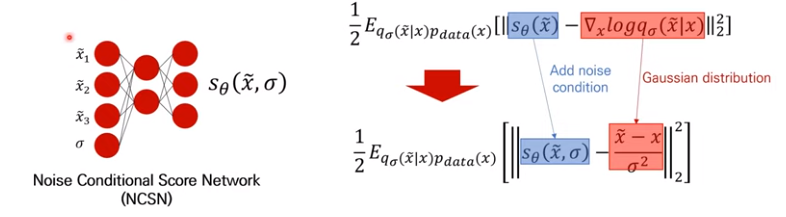
그래서 실제 Score Network의 구조도 바뀌었습니다. 입력값으로는 데이터$\tilde{x}$와 노이즈($\sigma$)를 넣어주고, 결괏값으로는 Score값이 뽑히게 만듭니다. 즉, $\sigma$가 얼만큼 데이터에 노이즈가 추가되었는가로 입력값으로 더 들어간 셈입니다. 이를 우리는 Noise Conditional Score Network(NCSN)이라고 합니다.

 

Loss function의 형태도 조금 바뀝니다. $s_{\theta}(\tilde{x})$가 이제 노이즈가 추가되었기 때문에,  $s_{\theta}(\tilde{x}, \sigma)$가 됩니다. 위 그림의 목적함수가 잘못되어서 아래의 논문에서 가져온 목적함수를 보겠습니다.

 

 

 

논문에서 $q_{\sigma}(\tilde{x}|x) = N(\tilde{x} | x, \sigma^2I);$이기 때문에, $\bigtriangledown_{\tilde{x}}log{q_{\sigma}(\tilde{x}|x)} = -\frac{\tilde{x}-x}{\sigma^2}$가 되어야한다고 되어있습니다. 이에 대한 간단한 증명은 위에 첨부했습니다.

 

그리고 $\lambda(\sigma_i) > 0$는 $\sigma_i$에 의존하는 coefficient function입니다. 그리고 이는 $||s_{\theta}(x, \sigma)||_2 \propto \frac{1}{\sigma}$로 설정합니다. 그 이유는 이렇게 하면, $\lambda(\sigma) = \sigma^{2}$가 되어,  위의 최종 식처럼 변형될 수 있기 떄문입니다. 이렇게 하면, $\frac{\tilde{x} - x}{\sigma} \sim N(0, I)$이 되고 $||\sigma s_{\theta}(x, \sigma)||_2 \propto 1$와 같이 정규화가 됩니다. 최종적으로 NCSN의 장점을 나열합니다.

 

• Adversarial training이 불필요합니다.
• Surrogate Losses가 불필요합니다.
• Sampling 할 때 contrastive divergence처럼 sampling과정이 필요없습니다.
• $s_{\theta}(x, \sigma)$는 tractable하기 때문에 특별한 VI처럼 Architecture가 필요없습니다. 
  • 특별한 $s$의 구조가 없으므로 어떤 모델이든 사용이 가능하다는 장점이 있습니다.

 

NCSN inference via annealed Langevin dynamics

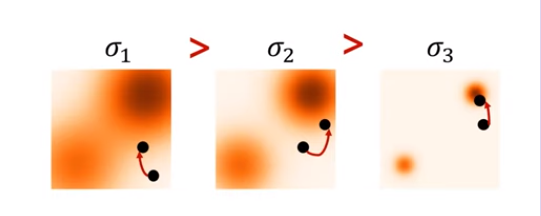
먼저, 확률값이 낮은 공간을 채우기 위해서 처음 $\sigma_1$값은 큰 값으로 둡니다. 그리고 $\sigma_2 > \sigma_3,...$으로 설정하여 점점 정확하게 퀄리티 높은 샘플링을 할 수 있도록 합니다. 이렇게 하는 이유는 $\sigma$가 너무 크면 분포를 많이 pertub하게되고, 그렇다고 너무 작다면 low density region을 많이 cover할 수 없기 때문입니다. Algorithm1을 보면, 2중 for문을 볼 수 있는데, 직관적으로 첫번째 for문은 Langevin dynamics에서의 scale을 담당하는 $\alpha_i$(Noise Schedule)를 gradually schedule 하고, 두번째 for문은 gradient ascent step을 1 -> T까지 진행하는 것을 볼 수 있습니다. 결국엔 $q_{\sigma_L}(x)$로 부터 $p_{data}(x)$에 근사한 샘플을 뽑을 수 있게 됩니다.

 

즉 $q_{\sigma_1}(x)$로부터 Langevin Dynamics를 진행하고, $q_{\sigma_2}(x)$, $q_{\sigma_3}(x)$으로 진행합니다. 그리고 한 단계에서 예측된 $\tilde{x_T}$는 다시 그 다음 단계에서의 $\tilde{x_0}$이 되어 저자들이 제안한 Annealed Lngevin dynamics를 수행하게 됩니다.

 

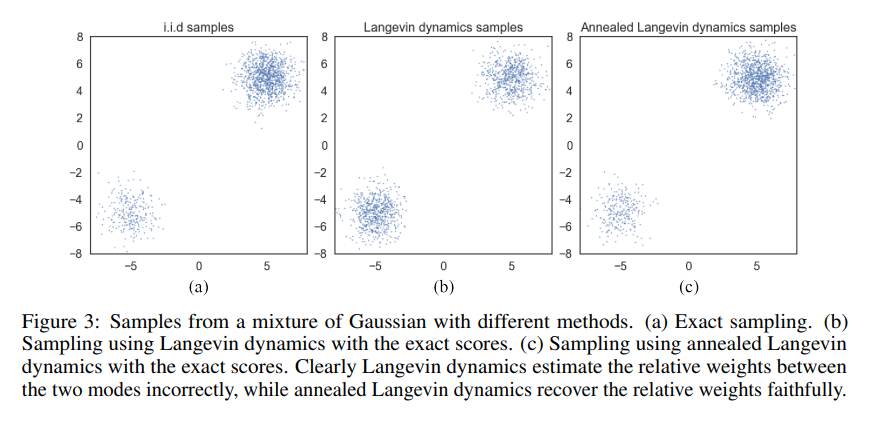
위와같이 Figure3의 (c)를 통해 Annealed Langevin dynamics sampling이 보다 정확하게 i.i.d samples과 비슷하게 sampling을 할 수 있음을 논문에서 확인할 수 있습니다.

 

각 단계의 noise scale이 다르다면, 각 단계마다의 목적 함수도 다를 것입니다. 그래서 각 단계마다 적절한 weight를 가해서 objective를 더해줄 필요가 있는데, 그렇기 때문에 우리가 위에서 $\lambda(\sigma_i) > 0$인 coefficient function을 통해 목적 함수를 통합했던 것입니다.

 

Experiments

NSCN을 통해 이미지를 생성하면, GAN과 비슷한 성능의 IS, FID값을 냈다는게 주목할만한 포인트입니다. 하지만 그때는 GAN이 군림하고 있을 시기라 이러한 Score-matching 생성형 모델이 괄목당했지만, 지금에야 Diffusion모델이 GAN의 성능을 이기면서 재평가 되고 있습니다.

NCSN vs DDPM

Training

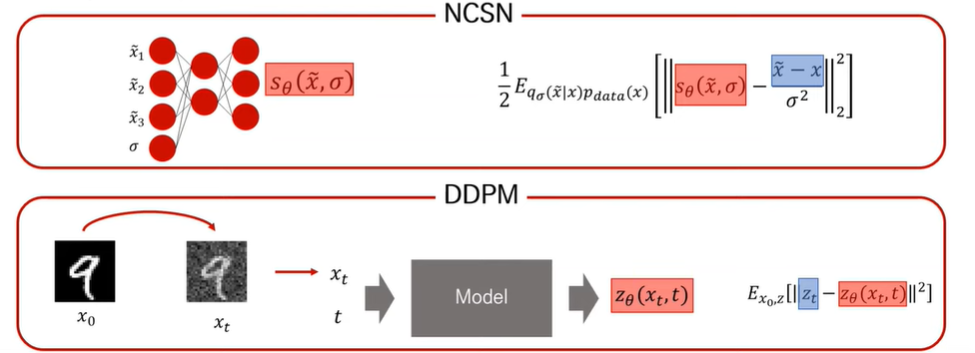
이제는 해당 논문(Score-Based Generative Modeling Through SDE, ICLR 2021, Song. et.al.,)을 볼 시간입니다. 생각해보면, NCSN과 DDPM의 훈련과정은 어느정도 유사하고 목적함수도 비슷한 것을 생각해볼 수 있습니다. 둘 다 노이즈가 추가된 데이터를 받아서 출력값을 내게됩니다. 그리고 모델의 출력값과 랜덤 노이즈를 맞추어 나가는 식으로 학습이 됩니다. --> Score-Matching으로서 동일하지 않을까?

 

Testing

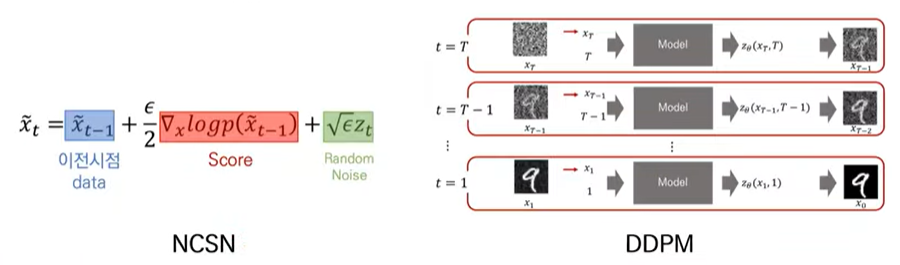
위와같이 sampling과정에서 특정 $t$시점의 데이터로부터 $x_0$데이터를 샘플링해내는 과정또한 유사하다고 볼 수 있습니다. --> Langevin Dynamics으로서 동일하지 않을까?

 

해당 논문에서는 NCSN, DDPM등이 SDE라는 framework안에서 통합될 수 있음을 주장합니다. 그 전에 ODE과 SDE에 대해 간단히 살펴보겠습니다.

 

ODE and SDE

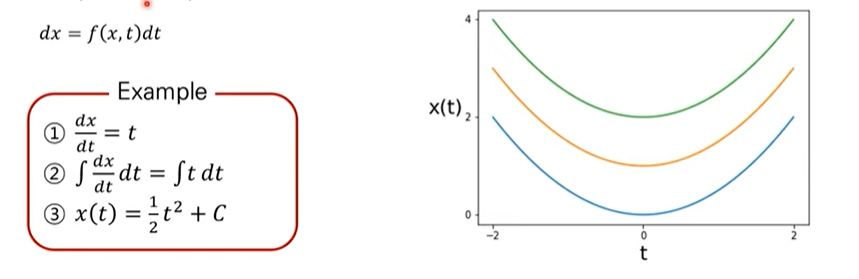
ODE는 상미분방정식을 나타내며, ODE -> Solve -> x(t)를 통해 진행됩니다. 이는 미분방정식인데, 변수가 하나인 것을 상미분방정식이라고 합니다. 예를 들어 $dx = f(x, t)dt$와 같은 꼴입니다.

 

이러한 미분방정식을 구하는 방법은, 위의 예시와 같이 적분을 취해서 해를 구하는 방법이 있습니다. 상미분 방정식의 해인 $x(t)$는 $C$에 따라 여러 함수가 될 수 있다는 특징이 있습니다.

 

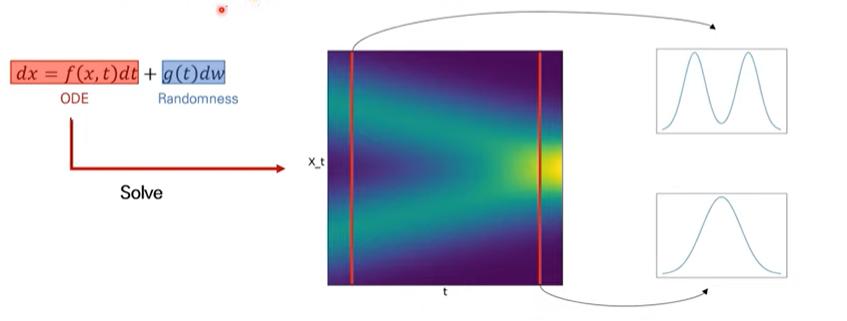
SDE는 확률미분방정식을 말합니다. 이 또한, SDE -> Solve -> $\{X_t\}$(Random process)와 같은 해를 통해 진행됩니다. ODE와 비슷하게, SDE에서도 해를 찾는다라는 것은 어떠한 랜덤 프로세스를 찾는다라고 할 수 있겠습니다. DDPM에서도 마르코프체인과 같이 랜덤 프로세스를 찾았는데, 이들은 확률변수들의 나열입니다.

 

위와같은, SDE의 해를 풀게되면 위와같은 확률분포들이 나열된 형태(랜덤 프로세스)를 찾을 수 있습니다.

 

Score-based Generative Modeling with SDEs

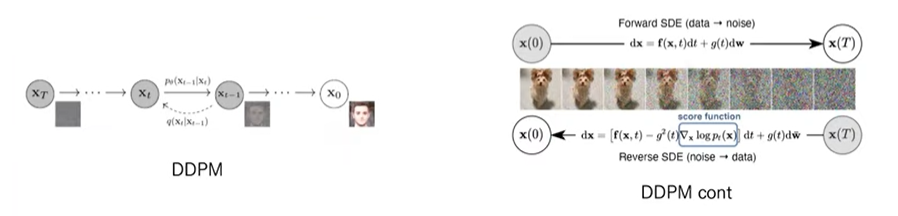
해당 논문에서 제안하는 것은 즉, NCSN/DDPM의 continuous한 버전이라고 할 수 있습니다. DDPM에서 Forward SDEs는 노이즈를 추가하는 과정, Reverse SDE는 노이즈를 제거하는 과정입니다. 여기서 Reverse SDE에 score function이 존재하게 됩니다.

 

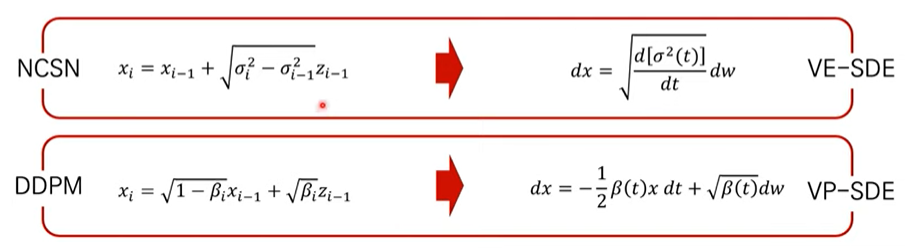
NCSN, DDPM의 forward process를 왼쪽과 같이 볼 수 있습니다. 그리고 이에 대한 SDE를 오른쪽과 같이 서로 다르게 유도할 수 있습니다. 그래서 해당 논문에서는 위와같은 형태의 SDE를 VE-SDE를 말하는 것이며, NCSN을 지칭합니다. 그리고 아래와같은 형태의 SDE를 VP-SDE를 말하는 것이며, DDPM을 지칭합니다. 

 

NCSN의 VE-SDE는 결국에 $t \rightarrow \inf$일 때, variance가 exploding합니다. 하지만 DDPM의 VP-SDE은 variance를 preserve한다는 특징이 있습니다.

 

그리고 논문에서는 NCSN++ cont, DDPM++ cont를 만들었는데, 이는 네트워크의 깊이를 더 깊게 쌓은 모델이라고 합니다.

 

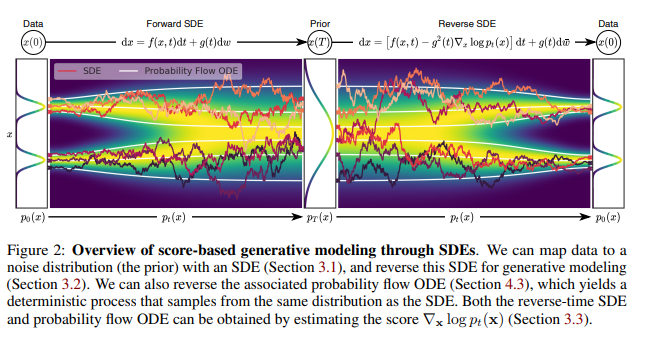
결국에 이미지를 sampling한다는 것은 위에서 말한것처럼 Reverse SDE를 푸는 것이라고 할 수 있습니다. SDE를 풀 수 있는 solver들에는 Euler-Maruyama, Runge-Kutta,... 등과 같은 여러가지 solver가 있습니다. 

 

그리고 해당 논문에서는, Reverse SDE를 푸는것에 그치지 않고, Predictor, Corrector라는 개념을 개재합니다. Predictor는 Reverse SDE를 풀어서 데이터를 생성하는 것을 말하며, Corrector는 생성된 데이터에 Annealed Langevin dynamics를 적용하는 과정을 말합니다. 저자들은 이러한 과정을 거치면 휴리스틱하게 샘플 퀄리티가 좋아졌다고 합니다.