[ 딥러닝 논문 리뷰 - PRMI Lab ] - Denoising Diffusion Probabilistic Model (DDPM)

Generative model에 있어서 이전에 GAN, VAE, Normalizing Flow모델등을 알아봤었습니다. 요즘에는 DDPM이 GAN보다 성능이 좋다고 들었습니다. 원래는 StyleGan을 통해 발전된 GAN에 대해 알아보려고 했으나, DDPM의 매력에 못이겨 바로 다음 포스팅에서 다루어보겠습니다. 

논문과 코드입니다. DDPM의 논문에는 아직 학부 3학년이 이해하기에는 벅찬 수식들과 많은 배경지식이 필요했습니다. 하지만 차근차근 필요한 내용을 정리하며 코드까지 짜보며 왜 DDPM이 현재 트렌드인 것인지 자세히 파헤쳐 보도록 하겠습니다. 추후에는 Diffusion관련 Multimodal 프로젝트를 해보고 싶은게 제 큰 목표입니다. 그 전에 도움을 많이 받은 동영상을 첨부하겠습니다.

Introduction

 

위와같이 Diffusion모델은 Gan모델을 이미 뛰어 넘었고 다양한 논문에 소개되었습니다.

 

DDPM의 intuition은 Physics에서 시작되었습니다. diffusion은 확산을 말하는데, 연기가 확산되는 것과 비슷한 원리입니다. 그리고 이전의 논문에서 작은 sequence에서의 확산은 forward와 reverse모두 Gausian일 수 있다는 것이 증명되었습니다. 즉 Gausian분포 안에서 다음 입자 위치가 결정되는 것입니다.

 

과정은 생각보다 간단하고 직관적입니다. 원본 이미지에서 Gaussian 노이즈를 만들어 버리는 forward process와 Gaussian 노이즈에서 확률적으로 이미지를 만들어 버리는 reverse process가 DDPM의 원리입니다. forward process는 input에 가우시안 노이즈를 Stochastic 하게 추가합니다. reverse process는 noise를 제거하는 분포를 forward로 부터 학습하는 것입니다. 그리고 이 모든것들은 Markov-Process로 진행된다는 것도 DDPM의 큰 특징입니다. 추후에 알아볼 DDIM은 Non Markov-Process로 진행되어서 특정 noise와 이로부터 생성되는 이미지가 1:1로 대응된다는 특징이 있어 더 많이 쓰이는 모델이라고 합니다.

 

Forward Diffusion Process

 

그림을 보면 이해하기 쉽습니다. 이에 대한 forward process를 수식으로 표현하면 아래와 같이 됩니다.

$$q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathsf{I}) Eq($$

$$q(x_{1:T}|x_0) = \prod_{t=1}^{T}q(x_t|x_{t-1})$$

 

해당 수식을 우리는 Diffusion process라고도 부릅니다. 여기서 두번째 수식을 보면 likelihood와 같은 식이라는 것을 알 수 있습니다. 그리고 이는 gaussian distribution에서 값을 뽑아낸다는 것도 알 수 있습니다. 해당 수식은 Bayes's Theory와 Markov-chain property를 통해 증명이 가능합니다.

 

또한, $ \sqrt{1-\beta_{t}} x_{t-1} $는 이미지 픽셀 값을 약간 감소시키는 역할을 하고, $ \beta_{t} \mathsf{I}$는 노이즈를 조금씩 계속 더한다는 것을 알 수 있습니다. 이렇게 해주는 이유는 최종적으로 만들어진 $x_T$를 gausian distribution으로 만들어 주기 위함입니다. 이에 대한 증명은 $Var(\sqrt{1-\beta_t})^2 + \beta_t)$의 분산은 1이고, 1보다 작은 scaling값을 계속 곱하니까 평균은 0으로 수렴하게 됩니다.

 

DDPM에서 $\beta_T$는 t마다 다르지만 기본적으로 학습되는 variable이 아닌 constant입니다. 그리고 $\beta_1 < \beta_2 < ...< \beta_T$입니다. 그 이유는 $\beta_0$으로 갈수록 추가되는 noise가 작아져야 이미지를 제대로 Generate할 수 있기 때문입니다.  추후에 나온 논문에서 beta값을 schedule하는 다양한 방법론들이 나왔습니다.

 

하지만 위의 방법에는 한가지 단점이 있습니다. $x_0$에서 $x_T$로 전개할 때, 모든 수식을 step by step으로 전개해야 해서 많은 memory를 소모하게 되고, 시간도 그만큼 오래걸린다는 단점이 있습니다. 그렇기에 이를 한번에 계산할 수 있는 shortchut을 수식적으로 만들 수 있습니다.

 

위와같이 $\bar{\alpha_t}$를 정의해서 간단히 정의할 수 있습니다. 이는 하나의 diffusion kernel이라고 할 수 있겠네요. 이또한, 그냥 쫙 전개한다음에 식을 풀어내면 간단히 증명할 수 있습니다. 당연히 diffusion kernel인 $q(x_T|x_0)$은 $ \bar{\alpha_t} \rightarrow 0$이므로 Gaussian distribution에 approximate된다는 걸 알 수 있겠네요.

 

Generative Learning by Denoising

 

우리는 위의 수식처럼 $q(x_0, x_t)$를 $x_0$에 대해 적분한 식에 대해서 $q(x_t)$ distribution을 구할 수 있습니다. 해당 식에서 $q(x_0, x_t)$(joint dist.)는 $x_0$과 $x_t$가 동시에 특정 값을 취할 확률을 의미합니다. 이는 DDPM의 확산 과정에서 초기 상태에서 시작하여 t시간만큼 확산된 상태에 도달하는 확률을 의미합니다. 그리고 $x_0$에 대해 적분하여 주변 확률 분포 $q(x_t)$를 얻게 되는데, 이는 $x_t$의 값이 관찰되었을 때에, 초기 상태 $x_0$의 구체적인 값에 관계없이 $x_t$가 특정 상태에 도달할 확률을 의미합니다. 즉 $q(x_t)$에서 $x_t$를 샘플링할 수 있다는 것이지요.

 

 결국 $x_0 ~ q(x_0)$을 샘플링 한다음에 $q(x_t | x_0)$인 diffusion kernel을 곱해 $q(x_t)$(Diffused data dist)를 구해서 t시간에서의 $x_t$를 샘플링할 수 있다는 것이죠.

 

Reverse Process

 

이제 reverse process를 생각해 보아야 합니다. 이의 목표는 $x_{t-1} ~ q(x_{t-1}|x_t)$을 반복적으로 샘플링하여 $x_0$을 구하는 것을 목표로 합니다. 여기서 $q(x_{t-1}|x_t)$는 Gaussian distribution을 따름을 예전에 증명되었다고 했었으므르로 $q(x_{t-1}|x_t)$의 mean과 std를 구하는 것을 목표로 해야할 것입니다.

 

하지만 해당 distribution은 일반적으로 intractable하므로, 우리는 각각의 forward diffusion step을 통해 approximate해야 합니다.

 

위와같이, 우리가 알아야 하는 것은 $\mu_{\theta}(x_t, t)$(mean)과 $\sigma_{t}^2$(variance)일 것입니다. DDPM에서는 $\mu_{\theta}(x_t, t)$만 trainable variable이므로 U-net이나 Denoising Autoencoder를 통해 학습하게 됩니다. 일반적으로 $\sigma_{t}^2$는 추후에도 보겠지만 $\beta_t$로 고정하게 됩니다.

 

그리고 reverse process를 표현하는 식을 오른쪽 수식과 같이 표현할 수 있게 됩니다. 이 또한, 뒤에서 더 자세히 알아보겠습니다.

 

Learning Denoising Model

이제 $\mu_{\theta}(x_t, t)$ 을 구하기 위해 모델을 학습해야 합니다. 이때 논문에서는 Variational upper bound를 통해 구하게 되는데 이는 VAE에서 사용한 방식과 동일합니다. 

 

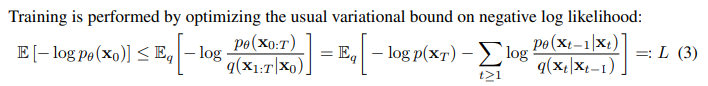
ELBO를 구하기 위해 negative log likelihood를 통해 수식을 풀어내면 위와같은 식을 만들어낼 수 있게됩니다. 그리고 Sohl-Dickstein et a. ICML 2025, Ho et al. NeurlPS 2020에 해당 수식이 아래와 같은 Loss식으로 된다는 것을 증명했죠.

 

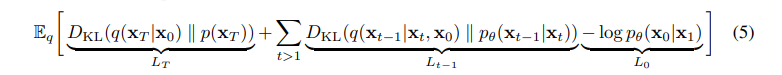
위 Loss term은 3개의 KL-divergence 식으로 이루어져 있으며, 위 3개의 식을 최소화하는 Regression 문제로 바라볼 수 있겠습니다. 그리고 각 term의 의미는 아래와 같은 의미를 가지고 있습니다.

• $L_T$: $x_0$으로 $x_T$를 생성하는 q분포와 $p(x_T)$가 유사해지도록 합니다.
  • 어차피 DDPM에서는 $B_t$가 constant이므로 forward process인 posterior distribution $q$는 learnable parameter가 없게 되어 constant로 남게됩니다.
• $L_{t-1}$: reverse process와 diffusion process간의 분포가 유사해지도록 합니다.
  • 우리는 이 식을 parameterizing을 통해 간단히 풀어낼 것입니다.
• $L_0$: reconstruction loss로서 $x_1$에서 $x_0$가 나올 likelihood를 최대화 시킵니다.

 

우리는 $L_{t-1}$의 $q(x_{t-1}|x_t, x_0)$을 봐야하는데, 이는 tractable posterior distribution입니다. 

 

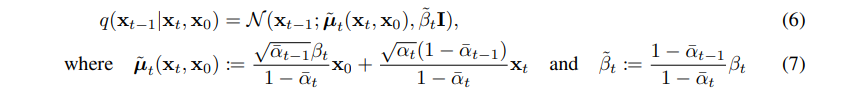
이 또한, 수식을 풀어내면 증명 가능합니다. 먼저 ELBO를 만들어 내는 과정을 보면 아래와 같습니다.

(2) -> (3) 식에서 KL-divergence식이 빠지니까 부등호가 생길 수 있게 됩니다. 그리고 쭉쭉 위에서 정의한 식으로 정리하면 (6)과 같은 최종 ELBO식이 나오게 됩니다.

 

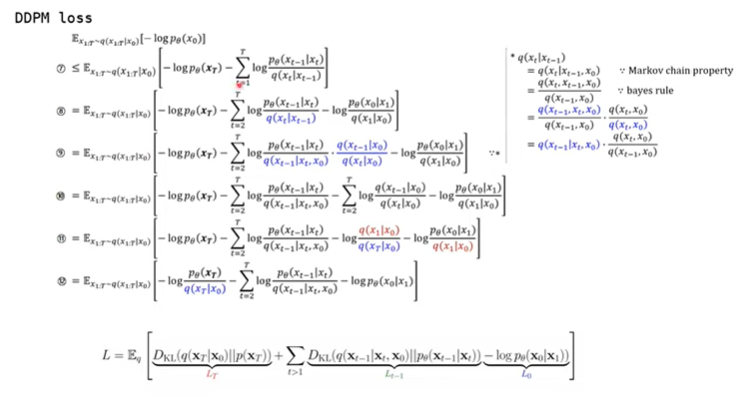
그 다음 과정도 비슷하게 Bayes' Rule과 Markov chain property를 통해 식을 풀어나가면 증명해 나갈 수 있습니다. 마지막으로 (7)과 같은 식이 어떻게 정의되는지는 아래와 같습니다.

 

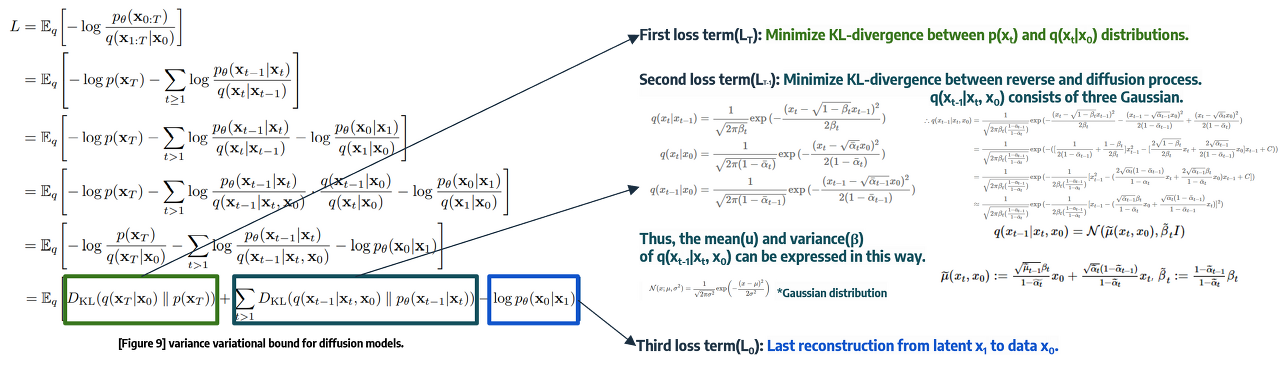
위와같이, 기본적인 Normal Distribution의 식을 통해 Bayes' Rule대로 끼워 맞춘다음에 맞춰주기만 하면 됩니다.

 

Parameterizing the Denoising Model

Reverse process (1<t<T)인 구간에서 DDPM의 분산과 관련된 조건입니다. $p_{\theta}(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}, \mu_{\theta}(x_t, t), \Sigma_{\theta}(x_t, t))$에서 $ \Sigma_{\theta}(x_t, t) = \sigma_t^2 \mathsf{I}$으로 정의했습니다.

 

그리고 위 그림처럼 $\sigma_t^2$를 각각 $\beta_t, \tilde{\beta_t}$로 초기화 했는데, 각각 전자는 $x_0$이 $\mathcal{N}(0, \mathsf{I})$로 수렴하고 후자는 one point에 deterministic하게 수렴했다고 합니다. 

 

두 번째는 $\mu_{\theta}(x_t, t)$의 표현방식입니다. 

 

$L_{t-1}$식을 정리한 결과입니다. 위 식은 $p_\theta(x_{t-1}|x_t)$과 $q(x_{t-1}|x_t, x_0)$이 Normal distribution이기 때문에, KL-divergence식을 간결하게 낼 수 있습니다. 해당 식에 대입하고 $\theta$와 관련없는 term을 $C$로 빼 버린 결과입니다.

 

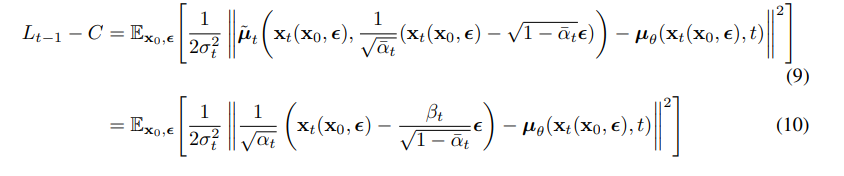
그리고 (8)번 식을 $x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}z$에 대해 정리한 다음에, (7)식을 활용해 reparameterizing을 한 결과입니다. 그리고 (10)식을 보면 $p$ 분포의 평균이 $q$분포의 평균을 예측하는 것이라고도 생각해 볼 수 있을것입니다.

 

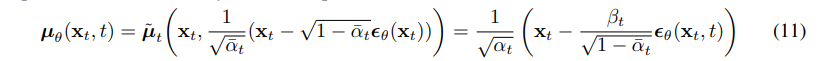
여기서 $x_t$는 model의 input으로 바로 나오는 값입니다. 그래서 $\epsilon_{\theta}(x_t)$를 정의해주었는데, 이는 $x_t$로 부터 forward proces의 $\epsilon$을 예측하는 function이라고 할 수 있습니다. 즉 우리는 $\epsilon_{\theta}$ function을 수렴할때까지 training을 시켜주기만 하면 된다는 것입니다. 그리고 (10)식은, (11)을 통해 정리하면 (12)와 같이 깔끔히 정리될 수 있습니다. 추가적으로 $\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha_t})}$은 DDPM에서 1로 설정됩니다. 그 이유는 Ho et al. NeurlPS 2020에서 이렇게 간단히 설정했을때, 좋은 성능을 냈기 때문입니다.

 

추가적으로 adcance weighting방법은, Choi et al. Perception Prioritized Training of Diffusion Models, CVPR 2022이나 Karras et al., Elucidating the Design Space of Diffusion-Based Generative Models, arxiv prepring 2022에서 살펴볼 수 있습니다.

 

 

결국 Sampling도 같은 맥락에서 진행될 수 있습니다. (6)식의 평균과 분산이 정해졌으므로 해당 분포로부터 VAE처럼 reparameterizing trick을 통해 sampling하면 됩니다. 이 식을 정리하자면, $x_t$가 주어졌을 때 $x_{t-1}$을 만들기 위해서 필요한 $\epsilon$값을 예측하는 방향으로 design하는 $ \epsilon_{\theta} $을 구하자! 입니다.

 

이와같이 pseudo code를 볼 수 있습니다. Training은 $q(x_0)$에서 $x_0$을 sampling한다음에, 일양분포 t를 sampling하고 $\epsilon$을 표준 정규분포로부터 sampling합니다. 그리고 수렴할때까지 (12)식을 기반으로 수렴할때까지 Training을 시켜주면 됩니다. Sampling은 표준 정규분포로부터 noise $x_T$를 sampling하고 T ~ 1까지 t>1인 동안 z를 표준 정규분포로 sampling 하고 (6)식에서 reverse process의 값을 sampling을 순차적으로 한다음에 $x_0$을 생성해내면 됩니다.

 

Implementation Considerations

 

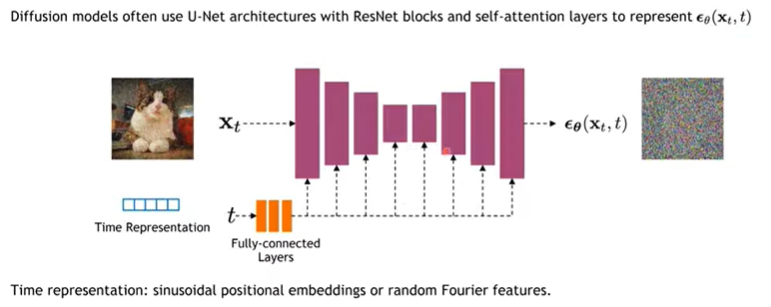
위와같이 Diffusion모델은 U-Net을 통해서 $\epsilon_{\theta}(x_t, t)$를 표현하게 됩니다. 먼저 U-net에 $x_t$를 집어넣습니다. 이때 time stamp $t$를 fully-connected layer에 넣어서 만든 embedding값을 추가적으로 skip-connection으로 추가해줍니다. 이를 통해서 어떤 noise가 $x_0$으로부터 추가되었던 건지 예측합니다.

 

실제로 U-Net 사이사이에는 self-attention, Group Normalization등등도 들어가있지만 그런 detail한 부분은 code에서 살펴보겠습니다. 

 

Diffusion Parameters & Content-Detail Tradeoff

 

$\beta_t$는 이미지에 noise를 추가하는 파라미터 였습니다. 이에 많은 논문에서 이러한 $\beta_t$를 schedule하는 방법론을 소개하고 있습니다. 또한, reverse process에서 $\sigma_t^2$를 정의하는 방법을 다르게 하는 많은 논문이 있으니 살펴보시기 바랍니다.

 

이러한 $\beta_t$가 중요한 이유는, $x_T$에서 $x_0$으로 가는 과정에서, 처음부분은 어떤 object의 윤곽을 만들어 나가는 과정입니다. 이를 low-frequency content를 만들어 내는 것이라고 합니다. 반면에 마지막 $x_0$과 가까운 부분은 detail한 부분을 수정해 나가는 부분인데, 이를 high-frequency content를 만들어 내는 것이라고 합니다. 이에 timesteps마다 곱해지는 $\beta_t$에 따라 이러한 역할이 영향을 받기 때문에, schedule하는 것은 매우 중요하다고 할 수 있습니다.

 

Loss function

기존의 Diffusion보다 loss function이 매우 간단해 졌습니다. DDPM에서는 $L_{1:T-1}$만을 신경써주면 되기 때문입니다. 이러한 이유는 $\beta_t$가 고정되어 있기 때문에 $L_t$를 신경쓸 필요가 없습니다.

 

추가적으로 $L_0$은 (13)와 같은 별개의 discrete decoder로 정의될 수 있습니다. 그래서 Loss term에 포함하지 않습니다. 

 

Experiments

 

실험 setting은 위와 같습니다. 위에서 다 설명한 내용들이니 수치적인 내용만 보시면 될 것 같습니다. 바로 실험 결과를 보겠습니다. 실험 metric은 생성 모델이 만들어낸 이미지와 실제 이미지 간의 통계적 거리를 측정한 FID를 통해 생성된 이미지의 다양성을 평가합니다.

 

그리고 아래는 $t$를 다르게 했을 때의 이미지 quality를 평가한 것입니다.

 

이 외에도 $x_0, x_0^{\text{'}}~q(x_0)$를 latent space에서 sampling합니다. 그 후, 주어진 소스 이미지로부터 잠재 공간의 특정 시점 t에서의 이미지 $x_t, x_t^{\text{'}} ~q(x_t|x_0)$를 생성합니다. 그 후 선형적으로 interpolation된 latent state $\bar{x_t}=(1-\lambda)x_t + \lambda x_{t}^{\text{'}} $를 reverse process를 통해 이미지 공간으로 다시 decoding합니다. 이와같은 reverse process는 선형적으로 interpolation된 latent space로부터 고품질의 이미지를 재구성하며, 소스 이미지의 변형된 버전에서 선형적으로 interpolation할 때 발생하는 artifact를 제거합니다. 

 

여기서 $\lambda$는 $x_0, x_0^{\text{'}} $사이의 속성을 다르게 반영하게 해주는 하이퍼 파라미터 입니다. 또한, 더 큰 $t$값은 더 거친(interpolation이 coarse한) interpolation을 생성할 수 있습니다. 반면 작은 $t$값은 더 세밀한 재구성을 가능하게 합니다.

DDPM에 대해 알아보았습니다. 그 다음에는 DDPM에 대한 이해도를 높이고자 코드로 구현해 보겠습니다. 코드로 구현한 후에는 DDIM, styleGAN, styleGAN2순으로 논문을 읽어보도록 하겠습니다.