[ 딥러닝 논문 리뷰 - PRMI Lab ] - DENOISING DIFFUSION IMPLICIT MODELS (DDIM)

DDPM을 쓰고 많은 시간이 흘렀습니다. DDPM은 가우시안 분포에서 추출한 noise를 마르코프 체인 과정으로 순차적으로 걷어내며 sample을 생성해내는 Generative Model이였습니다. 하지만 이 방법은, 순차적으로 reverse-process를 진행해야 해서, step에 따른 시간이 많이 소요되었습니다. 그래서 GAN에 비해 sampling quality는 높았지만, 그만큼 sampling속도가 느리다는 단점이 있었습니다. 오늘 살펴볼 DDIM은 이러한 제한을 Non-Markovian Process를 통해 해결했으며, Objective Function은 DDPM과 똑같이 가져가서 DDPM(training) -> DDIM(sampling)이 가능해지게 되었습니다. 논문 링크, 깃허브 링크입니다.

 

1. Introduction

DDPMs는 adversarial training을 사용하지 않고 high quality의 이미지를 만들어낼 수 있는 방법입니다. 하지만 이에 따른 단점도 매우 많죠. 단점인 sampling speed를 높이기 위해 DDIMs를 제안합니다. 이는 DDPMs와 동일한 training procedure를 사용해 더 효율적인 학습과 샘플링을 가능하게 합니다. DDPMs에서 Markovian diffusion process로 정의된 diffusion process를 DDIMs에서는 Non-Markovian process로 일반화 했습니다.

 

이러한 DDIMs의 특징으로는 generative process가 deterministic하게 진행될 수 있다는 점과, 더 빠른 속도로 더 높은 퀄리티의 이미지를 생성해 낼 수 있다는 점입니다. 이는 경험적으로 DDPMs과 비교했을 때 10x, 50x더 빠른 샘플링 속도를 제공할 수 있다고 합니다. 그리고 semantic하게 latent space로부터 image interpolation을 가능해진다는 장점이 있다.

 

이제부터 수식을 볼것인데,, 일일이 입력하기 귀찮아서 논문에 있는 수식을 그대로 첨부하겠습니다.

2. Background

우리는 당연히 $q(x_0)$이라는 실제 data분포가 있을때, $p_{\theta}(x_0)$을 근사해서 알고자 하는 것입니다. 그래서 우리는 DDPMs의 latent variable model을 위와같은 꼴로 나타낼 수 있는 것입니다. 

 

그리고 $x_0$와 같은 latent space에 있는 variable $x_1,...x_T$을 $X$라고 표기합니다. 여기서 $\theta$는 $q(x_0)$의 variational lower bound를 최대화 하기 위한 학습 파라미터 입니다. 그리고 이를 풀어쓰면 위와같은 Equation(2)를 볼 수 있습니다. 

 

그리고 $q(x_{1:T}|x_0)$은 inference distribution입니다. DDPMs에서는 이를 훈련시키지 않고, 고정(fixed)시켜놓았었습니다. 여기서 latent variable은 매우 높은 차원을 가지고 있습니다. Equation(3)은 DDPMs에서도 소개한 Shortcut이였습니다. 

 

위와같이 marginal distribution $q(x_t|x_0)$을 구할 수 있었고, 정규 표현식으로 $\alpha_{1:T}$를 활용하여 표현할 수 있었습니다.

 

최종적으로 $\epsilon$을 활용하여 $x_t$를 $x_0$에 대해 linear combination형태로 표현할 수 있었습니다. 이는 매우 많이 활용되는 수식이므로 확실히 알아두시는걸 추천합니다.

 

우리가 $\alpha_T$를 0에 근접하게 설정해놓으면 최종적으로 모든 $x_0$에 대해서 $q(x_T|x_0)$은 Standard Gaussian으로 수렴하게 됩니다. 그래서 우리가 $p_\theta(x_T) := {N}(0, I)$으로 설정하는건 아주 자연스러운 것이죠.

 

모든 확률 조건식을 train가능한 mean functions인 Gaussian으로 고정하면 위와같은 Equation(5)와 우리가 최적화해야할 Obejctive function이 나오게 됩니다. 참고로 DDPMs에서 학습된 모델의 생성 performance를 극대화 하기 위해 $\gamma = 1$인 obejctive로 최적화 했습니다. 훈련된 모델에서 $x_0$은 이전 $p_\theta(x_T)$에서 $x_T$를 샘플링한 다음 반복적으로 reverse process에서 $x_{t-1}$을 샘플링합니다.

 

forward process에서 T는 중요한 hyperparameter입니다. Variational 관점에서 T가 커질 수록 reverse diffusion process가 Gaussian에 근사하게 되고, reverse process는 그만큼 좋은 사전정보를 가지고 있으므로 근사치가 좋아지게 될 것입니다. 

 

3. Variational Inference for Non-Markovian forward processes

DDPM의 obejctive인 $l{L}_{\gamma}$가 marginal distribution인 $q(x_t|x_0)$에만 의존하고, joint distribution인 $q(x_{1:T}|x_0)$에는 직접적으로 의존하지 않는다는 것을 알 수 있습니다. 이러한 intuition을 확률적으로 생각해보면, 같은 marginal distribution을 가지는 다양한 inference distribution(joints)가 있습니다. 그래서 DDIMs은 아래와 같은 Non-Markovian으로 이루어진 generative process를 이끌어 냈습니다. 이러한 접근 방법은 Non-Markovian 관점이 Gaussian case에 적용될 수 있다는 것을 보일 것입니다.

 

3.1. Non-Markovian Forward Process

 

* Marginal distribution, joint distribution

marginal distribution과 joint distribution에 대해 자세히 알고 싶다면 

https://blog.naver.com/mykepzzang/220837645914을 참고하시기 바랍니다.

위와같이 DDPMs의 object의 marginal distribution을 맞추어 주려면, DDIM의 inference(forward) distribution의 mean function은 위와 같아야 합니다($\sigma = 0$으로 정의된다면  forward process도 deterministic해집니다). 그리고 Equation(6)의 summation부분을 Baye's rule을 사용해서 전개하면 아래와 같은 forward process를 얻을 수 있게 됩니다. 

 

Equation(8)은 DDPMs에서 본적 있던 식입니다, 다만 쓰이는 목적이 다릅니다. 여기서 DDIMs의 forward process는 DDPMs과 다르게 $x_0$이 joint condition으로 붙어서 Equation(3)과는 다르게 Non-Markovian임을 알 수 있습니다. 여기서 $\sigma$는 forward process가 얼마나 stochastic한지를 컨트롤 하는 파라미터 입니다. 이가 0에 가까워 질수록 $x_{t-1}$값이 결정적(fixed)되어 최종적으로 생성되는 $x_0$의 값이 deterministic하게 됩니다.

 

3.2. Generative Process and Unified Variational Inference Objective

이제, 우리는 학습가능한 $p_\theta(x_{0:T})$를 정의합니다. 이때 $p_{\theta}^{(t)}(x_{t-1}|x_t)$는 아까 보았던 forward process인 Equation(8)의 지식을 최대한 활용하게 됩니다. 이를 직관적으로 이해하면 noisy한 $x_t$가 있을 때

 

1. 대응되는 $x_0$을 예측하고
2. Equation(8)의 식으로 그 다음 sample인 $x_{t-1}$을 얻는다고 생각하면 됩니다.

 

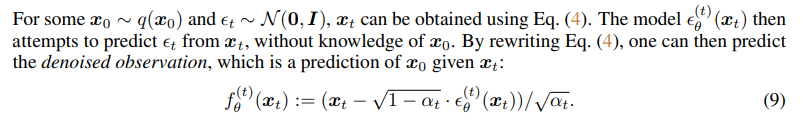
$x_0 \sim q(x_0)$와 $\epsilon_{t} \sim {N}(0, I)$에 대해 Equation(4)를 활용하여 $x_t$를 얻어낼 수 있습니다. 여기서 모델 $\epsilon_{\theta}^{(t)}(x_t)$는 오직 $x_t$로부터 $\epsilon_{t}$를 예측하게 됩니다. 이제 Equation(4)를 $x_0$에 대해 표현하게 되면 우리는 $x_t$에 대한 $x_0$의 예측 값인 denoised observation을 $\epsilon_{t}$을 통해서 알 수 있게 되는 것입니다.

 

그리고 fixed prior인 $p_{\theta}(x_T)$가 standard gaussian distribution이라는 것을 통해 generative process를 Equation(10)과 같이 정의할 수 있게 됩니다. 이를 정리하면 아래와 같습니다.

 

1. denoised observation
   1. Equation(4)를 $x_0$에 대해 표현해서 $x_t$로 $x_0$을 예측
2. generative process
   1. $q_{\sigma}(x_{t-1}|x_t, f_{\theta}^{(t)}(x_t))$에서는 $f$가 denoised observation으로서 $x_0$을 대체하게 됩니다.
   2. 그리고 항상 generative process를 보장하기 위해 $t=1$일 때, 가우시안 노이즈 $\sigma_1^2I$를 추가해주었습니다. --> $t=1$일 때에 forward process가 항등 함수꼴을 나타내기 때문에, generative process를 보장할 수 없기 때문임.

 

우리는 $\theta$를 variational inference objective에 대해서 최적화 시켜야 합니다. Equation(6), Equation(1)을 통해 식을 factorization했습니다. 

 

여기서 $\sigma$를 어떤 값으로 선택하느냐에 따라 다른 모델이 됩니다. 만약 $\sigma = 0$으로 둔다면, Equation(11)은 DDIMs의 objective function이 되며, $\sigma \ne 0$이라면 이 함수는 DDPMs의 objective function이 되게됩니다.

 

위와같은 정보를 활용하여 Theorem 1을 정의했습니다. (1) 만약 $\gamma = 1$이라면, objective function은 DDPM의 variational lowerbound와 같습니다. 또한, $J_{\sigma}$는 $L_{\gamma}$의 일종인데, 이는 $\gamma = 1$일 때 최적의 값을 가집니다. 그래서 Therem 1이 궁극적으로 하고싶은 말은, 모든 t에 대해서 $\epsilon_{\theta}$가 공유되지 않아도, $L_1$은 $J_{\sigma}$의 목적함수 또한 될 수 있다는 것입니다.

 

4. Sampling From Generalized Generative Process

Ho et.al(2020)에서 $\gamma = 1$로 두었을 때, optimal을 구할 수 있었으므로, 위에서 말한대로 $L_1$을 objective function으로 사용합니다. $\sigma$를 어떻게 설정하느냐에 따라 forward process를 markovian혹은 Non-markovian으로 학습시킬 수 있습니다. 여기서 주의해야할 점은 $\sigma$를 어떤 값으로 두냐와 상관없이 학습해야 하는 parameter는 $\theta$라는 점입니다. <-- 이 말 뜻이 뭐냐!

 

• markovian process로 학습시킨 DDPM 모델의 $\theta$를 DDIM의 generative process에도 활용할 수 있다. 그 이유는 위와 동일함.

DDIM은 이처럼 새로운 훈련 방법을 제시한 것이 아닌, diffusion process의 objective function을 Non-markovian process로 일반화하고, 좀 더 빠르게 이미지 생성이 가능하도록 새로운 sampling방법을 제시했다는 점에 있습니다. 그래서 요즘? 트랜드는 DDPM으로 학습시키고 DDIM의 일반화된 generation방식으로 sampling을 하는 것이라고 합니다.

 

4.1. Denoising Diffusion Implicit Model

Equation(10)의 $p_{\theta}(x_{1:T})$로부터 우리는 위의 Equation(12)식을 유도해낼 수 있습니다. Equation(12)는 $x_t$로 부터 $x_{t-1}$을 sampling하는 과정을 뜻합니다.

 

여기서 $\epsilon_{t} \sim N(0, I)$은 standard gaussian noise로서 $x_t$에 독립적인 값이고, 이로 인해 우리는 $\alpha_0 = 1$로 정의했습니다. 그리고 계속 말했다 싶이 $\epsilon$의 값에 따라서 서로 다른 generative process가 될 수 있습니다 (DDIM or DDPM). 당연히 $\epsilon_{\theta}$ 이 같은 모델을 공유하면서 서로 다른 generative process를 채택할 수 있습니다. <-- 재학습이 불필요!

 

• $\sigma_t = \sqrt{\frac{1-\alpha_{t-1}}{1-\alpha_{t}}} \sqrt{\frac{1-\alpha_{t}}{\alpha_{t-1}}}$ for all t
  • forward process = "Markovian" = DDPM
• 만약 $\sigma_t = 0$ for all t
  • forward process가 $x_{t-1}, x_0$에 대해 deterministic해집니다. ($t=1$ 제외)
  • $\sigma_t\epsilon_t$가 0이 되어서, model이 implicit probablistic model이 됩니다.
  • sample이 되는 과정이 fix되어서 fast sampling이 가능해집니다.

4.2. Accelerated Generation Process

DDPM에서는 generative process(=diffusion process)는 reverse process의 근사로 고려되었습니다. 이 때, forward process가 $T$ step만큼 필요하기 때문에, generative process도 sampling할 때 $T$ step이 필요했습니다. 하지만 DDIM의 denoising object인 $L_1$은 $q_{\sigma}(x_t|x_0)$이 고정되어 더 이상 forward과정과 상관이 없으므로, T보다 짧은 forward process도 고려해 샘플링 과정을 가속화하는 방안을 생각해볼 수 있을 것입니다. 

 

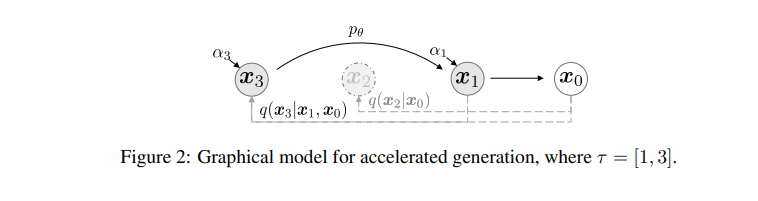
forward process가 모든 latent variables $x_{1:T}$가 아닌 subset${x_{\tau1, ..., x_{\tauS}}$에 대해 정의되어 있다고 합시다. $\tau$는 $[1, ...,T]$의 증가하는 증가 부분 시퀀스이며, 길이가 S입니다. 여기서 우리는 $q(x_{\taui}|x_0)$가 주변 분포에 부합하도록 sequential forward process를 위와같이 정의합니다.

 

generative process는 이제 $\tau$의 reverse순서대로 sampling합니다. 이를 우리는 sampling trajectory라고 합니다. 여기서 sampling trajectory가 $T$보다 짧을 때, 우리는 유의미한 computational efficiency증가를 달성할 수 있다고 말합니다.

 

Equation(12)에서와 같이 식의 약간의 변형만으로 Equation(10)에서와 같이 더욱 빠른 generative process를 얻어낼 수 있었고, 이를 DDPM/DDIM모두에 적용 가능합니다. 하지만, Figure2와 같이 sampling을 accelerate하면 기존보다 빠르게 이미지를 생성할 수 있지만, forward step의 임의의 step에서만 학습했기 때문에, generative process에서도 일부만 sampling할 수 있게 됩니다. 그러므로, subset으로 훈련된 모델은 기존(Ho et al.)에서 제안한 step보다 더 많은 continuous한 step에서 학습을 해야할 수 있다고 합니다.  

 

4.3. Relavance to Neural ODEs

DDIM의 iterate를 Equation(12)에 따라 작성할 수 있습니다. 이는 ODE를 풀기위한 Euler integration과의 유사성은 더 명백해졌습니다. 이에 대한 ODE를 작성하면 Equation(13)과 같고, Equation(14)을 따르는 Euler method로 다루어질 수 있게됩니다. 이는 충분히 Discretization steps를 거치면, Equation(14)의 ODE를 reverse해서 generation process의 reverse, 즉 encoding도 가능해집니다 ($x_0 \rightarrow x_T$). 이처럼 DDIM은 diffusion process을 연속적인 시간에 대한 ODE로 표현하여 더 부드러운 전환과 더 정밀한 제어를 가능하게 합니다.

 

5. Experiments

실험에서는, 더 적은 iteration 상황에서 DDIM이 DDPM보다 성능이 좋은지 실험적으로 확인합니다. 게다가 DDPM과는 다르게 $x_T$의 initial latent variables가 결정(fixed)되면, DDIM이 generation trajectory와 상관없이 항상 high-level의 이미지를 생성할 수 있으며, latent space상에서의 interpolation이 가능한지 확인하겠습니다.

 

각각의 dataset에 대해서, $T = 1000$에 대한 동일한 훈련된 모델을 사용합니다. 또한 Section 3에서 다룬 $L_1$의 objective function을 사용합니다. DDPM과 DDIM의 유일한 차이점은, 모델에서 sample을 어떻게 뽑는지에 있습니다. 우리는 $\tau$를 조절하고, $\sigma$를 조절해서 deterministic DDIM과 stochasitc DDPM을 만듭니다.

 

논문에서는 sub-sequence $\tau$ of $[1, ...,T]$와 다른 variance hyperparameter인 $\sigma$를 고려한다 했습니다. $\eta \in \mathbb{R}_{\geq0}$는 우리가 직접 control할 수 있는 hyperparameter입니다. $\eta = 1$이라면 DDPM, $\eta = 0$이라면 DDIM으로 할 것입니다. 추가적으로 DDPM에서 $\sigma(1)$보다 큰 $\hat{\sigma}:$standard deviation을 사용했을때의 결과도 실험합니다. 이는 CIFAR10 samples을 생성하기 위한 Ho et al.(2020)을 구현하기 위해 사용되었습니다.

 

5.1. Sample Quality and Efficiency

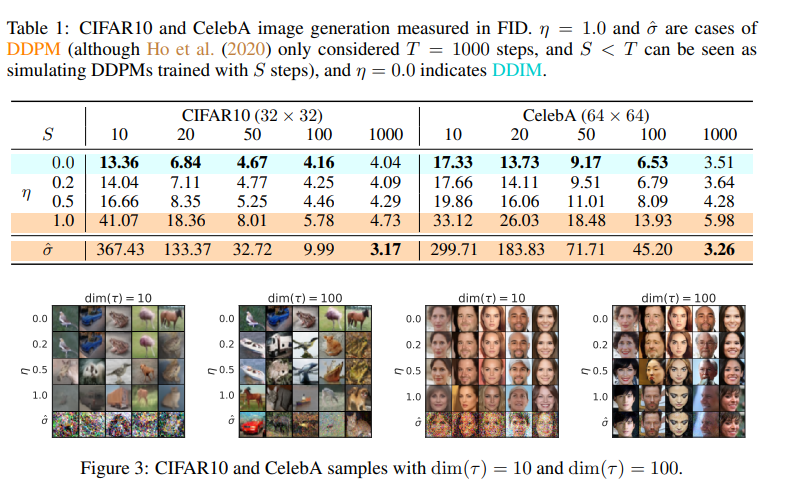
위 Figure3은 CIFAR10, CelebA에 대해 학습된 모델에 대한 FID Score입니다. sample quality는 $dim(\tau)$가 높을수록 높아지는 것을 볼 수 있습니다.

 

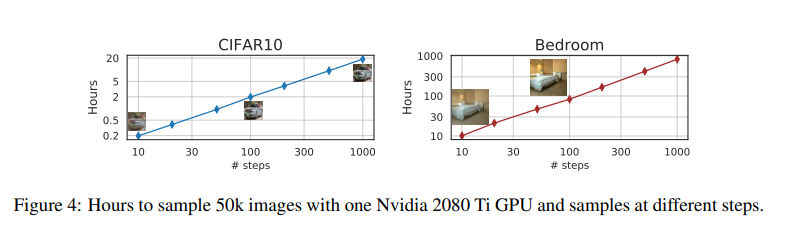
sample quality와 computational costs는 trade-off관계로서 같은 $dim(\tau)$에 대해 DDIM이 성능이 더 좋은 것을 볼 수 있습니다. 그리고 sample trajectory의 길이가 길어질 수록 generation에 필요한 시간이 선형적으로 증가하는데, DDIM이 더 효율적으로 샘플을 생성할 수 있음을 보여줍니다. 예를 들면, DDPM이 1,000step 정도 필요한 quality의 sample을 만들려면 DDIM은 20step이면 생성할 수 있고, 이는 DDPM대비 50배 빠른 속도임을 알 수 있습니다.

 

5.2. Sample Consistency in DDIMs

Figure5에서는 같은 $x_T$에 대해 다른 generative trajectories를 갖는 이미지들이 나와있습니다. 흥미로운점은 $x_T$같으면 대부분의 high-level feature가 generative trajectories와 상관없이 비슷하다는 점입니다. 대부분의 경우에서 20 steps을 통해서 sample을 만들때 이미 1000 steps로 sample을 만든경우와 high-level feature가 동일해지기 시작했습니다. 이는 $x_T$가 image의 latent encoding으로서 정보를 내포할 수 있음을 시사합니다.

 

5.3. Interpolation in Deterministic Generative Processes

Section5.2.에서 봤다싶이 DDIM sample의 high-level feature가 $x_T$에 의해서 encoding되므로, 저자들은 GAN(implicit probabilistic model)에서도 가능한 semantic interpolation이 가능함을 보이고 있습니다. $x_T$사이에서 두 샘플 사이의 interpolation이 가능함을 Figure6에서 보여주고 있습니다.

 

5.4. Reconstruction from Latent Space

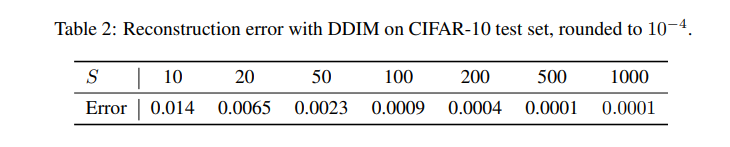
Section4에서 ODE에 대해 잠깐 다루었습니다. DDIM이 ODE로 Euler integration을 하므로, $x_0$을 $x_T$로 encoding하거나 반대로 reconstruction하는 것이 가능합니다. 또한, Neural ODE와 유사하게 sample trajectory length인 $S$가 커질수록 낮은 reconstruction error를 Table2에서 볼 수 있습니다.