DFS
이는 깊이 우선 탐색이라고도 하며, 루트 노드 ( 혹은 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 deep하게 탐색하는 방법입니다.
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사합니다.
- 즉, 넓게(wide)탐색하기 전에 깊게(deep)탐색 하는 것입니다.
- 사용하는 경우 : 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택합니다.
BFS
이는 너비 우선 탐색이라고도 하며, 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법입니다.
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
- 즉, 깊게(deep 탐색하기 전에 넓게(wide)탐색하는 것입니다.
- 만약에 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 사용합니다.
- Ex) 지구상에 존재하는 모든 친구 관걔를 그래프로 표현한 후 Ash와 Vanessa사이에 존재하는 경로를 찾는 경우
- 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모릅니다.
- 너비 우선 탐색의 경우 - Ash와 가까운 관계부터 탐색해야 합니다.
- 또한 너비 탐색이 깊이 우선 탐색보다 좀 더 복잡하게 됩니다.
/DFSBFS.c
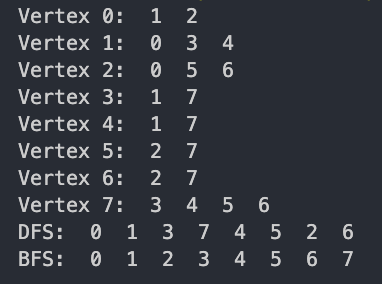
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_VERTEX 100 #define true 1 #define false 0 typedef struct node_ { int vertex; struct node_ *link; } node, *nodePointer; // queue를 위해 front와 rear를 선언해주어야 합니다. nodePointer front, rear; nodePointer queue[MAX_VERTEX]; // adjacent list nodePointer adjList[MAX_VERTEX]; short int visited[MAX_VERTEX]; void initNode(nodePointer *node, int vertex) { *node = malloc(sizeof(nodePointer)); (*node)->vertex = vertex; (*node)->link = NULL; } /** * @brief DFS를 시작 노드 v부터 시작한다. * */ void dfs(int v) { nodePointer w; visited[v] = true; printf(" %d ", v); w = adjList[v]; while (w != NULL) { // 방문하지 않았을 때만 dfs과정을 진행해 주는 것이 좋아 if (!visited[w->vertex]) dfs(w->vertex); w = w->link; } } void addq(int item) { nodePointer temp; initNode(&temp, item); if (!rear || !front) { front = rear = temp; } else { rear->link = temp; rear = rear->link; } } int deleteq() { int temp = front->vertex; front = front->link; return temp; } // bfs는 dfs와는 다르게 큐를 이용하여야 한다. void bfs(int v) { nodePointer w; front = rear = NULL; printf(" %d ", v); visited[v] = true; addq(v); while (front != NULL) { v = deleteq(); w = adjList[v]; while (w != NULL) { if (!visited[w->vertex]) { printf(" %d ", w->vertex); addq(w->vertex); visited[w->vertex] = true; } w = w->link; } } } int main(void) { FILE *fp_read = fopen("DFSBFS.txt", "r"); if (fp_read == NULL) { fprintf(stderr, "File Open Error!"); exit(EXIT_FAILURE); } int vertCount, data, check = false; fscanf(fp_read, "%d", &vertCount); // tempNode는 가장 뒤를 가리키게 하는 변수 nodePointer newNode, tempNode; // adjacent list를 구현해야 한다. for (int i = 0; i < vertCount; i++) { check = false; for (int j = 0; j < vertCount; j++) { fscanf(fp_read, "%d", &data); if (data == 1) { // data가 있는 곳이라면 initNode(&newNode, j); if (check == false) { // 일단 처음에 아무것도 안들어가 있다면 adjList[i] = newNode; tempNode = newNode; check = true; } else { tempNode->link = newNode; tempNode = newNode; } } } } for (int i = 0; i < vertCount; i++) { printf("Vertex %d: ", i); tempNode = adjList[i]; while (tempNode) { printf(" %d ", tempNode->vertex); tempNode = tempNode->link; } printf("\n"); } printf("DFS: "); dfs(0); printf("\n"); memset(visited, 0, sizeof(short int) * MAX_VERTEX); printf("BFS: "); bfs(0); printf("\n"); return 0; }
/DFSBFS.txt
8 0 1 1 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 1 1 1 1 0
시간 복잡도
dfs(x)는 x에 방문하는 함수이므로 정점의 개수, 즉 차수인 V번만큼 dfs(x)가 호출됩니다. 따라서 dfs(x) * 시간복잡도 * V가 전체 dfs알고리즘의 시간복잡도가 됩니다. 구현 방식에 따라 어떻게 다른지 구체적으로 알아보도록 합시다.
- 인접행렬에서의 시간복잡도
- 모든 정점을 다 찾아봐야 하기 때문에 dfs(x)의 시간복잡도는 O(V)
- dfs(x)가 V번 호출되어야 하므로 dfs알고리즘의 시간복잡도는 O(V * V) = O(V^2)
- 인접리스트에서의 시간복잡도
- 인접행렬과 마찬가지로 dfs(x)는 V번 호출
- dfs(x)의 시간복잡도는 O(V + E)
- 인접리스트에서 dfs가 호출되는 방법은 모든 정점을 다 찾는 인접행렬의 탐색방법과 많이 다릅니다.
- 또한 a[x].size()는 전체 간선의 개수가 아니라, 한 정점과 연결된 간선의 개수이기 때문에 dfs(x)의 시간복잡도는 O(E)가 아님을 확인해야 합니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Tree ( Forests ) (0) | 2022.05.31 |
|---|---|
| Data Structure - Tree ( Selection Tree ) (0) | 2022.05.31 |
| Data Structure - Tree ( BST ) (0) | 2022.05.31 |
| Data Structure - Tree ( Heaps ) (0) | 2022.05.31 |
| Data Structure - Hashing ( Dynamic Hashing ) (0) | 2022.05.30 |
