BST ( Binary Search Tree )
BST의 정의에 대해 간간히 정의하고 가겠습니다. 이는 비어 있을 수도 있습니다. 만약 비어 있지 않다면 다음과 같은 조건을 만족하게 됩니다. 각각의 노드는 하나의 key만을 가지고 있습니다. 그리고 tree안에 있는 모든 key들은 distinct즉 다 다릅니다. 그리고 left subtree 에 있는 모든 키는 root의 key보다 작아야 하고, right subtree에 있는 모든 키는 커야 합니다. 그리고 left와 right subtrees는 둘다 BST입니다. disjoint하다고 표현하죠

다음은 BST의 전형적인 예시입니다. 맨 왼쪽은 BST가 될 수 없는데 딱봐도 아니게 생겼습니다.
Insertion
이번에는 트리를 insert하고 이를 preorder, inorder, postorder로 결과를 출력하는 코드를 작성해 보도록 하겠습니다.
/BST.c
#include <stdio.h>
#include <stdlib.h>
typedef struct node_
{
int key;
struct node_ *leftChild;
struct node_ *rightChild;
} node, *treePointer;
treePointer iterSearch(treePointer tree, int k)
{
while (tree)
{
// 만약에 찾은 경우
if (k == tree->key)
return tree;
if (k < tree->key)
tree = tree->leftChild;
else
tree = tree->rightChild;
}
return NULL;
}
// 처음에는 null이 들어 올 것이다.
node *modifiedSearch(treePointer tree, int key)
{
// 만약 tree가 null이라면 그냥 return
if (!tree)
return NULL;
while (tree)
{
// 같으면 추가할 필요 없다
if (key == tree->key)
return NULL;
// 만약 추가 하고자 하는 키가 더 작다면
// 왼쪽으로 가야한다.
if (key < tree->key)
{
// 그러다 만약에 그 leftChild가 null이라면 그냥 추가할 노드를 return한다.
if (tree->leftChild == NULL)
return tree;
tree = tree->leftChild;
}
// 만약 추가 하고자 하는 키가 더 크다면
else
{
// 그러다 만약에 그 rightChild가 null이라면 그냥 추가할 노드를 return한다.
if (tree->rightChild == NULL)
return tree;
tree = tree->rightChild;
}
}
return NULL;
}
void insert(treePointer *node, int k)
{
treePointer ptr;
// 추가할 노드의 parentNode
treePointer temp = modifiedSearch(*node, k);
// node가 null인 경우도 처리를 해주어야 한다. -> head가 null이게 되면 그냥 할당만 하고 반환
if (temp || !(*node))
{
ptr = (treePointer)malloc(sizeof(*ptr));
ptr->key = k;
ptr->leftChild = ptr->rightChild = NULL;
if (*node)
{
if (k < temp->key)
temp->leftChild = ptr;
else
temp->rightChild = ptr;
}
// 만약에 node가 있지 않다면 그냥 ptr을 만들어서 반환해 줘야 한다.
else
*node = ptr;
}
}
void inorder(treePointer ptr)
{
if (ptr)
{
inorder(ptr->leftChild);
printf(" %d ", ptr->key);
inorder(ptr->rightChild);
}
}
void preorder(treePointer ptr)
{
if (ptr)
{
printf(" %d ", ptr->key);
preorder(ptr->leftChild);
preorder(ptr->rightChild);
}
}
void postorder(treePointer ptr)
{
if (ptr)
{
postorder(ptr->leftChild);
postorder(ptr->rightChild);
printf(" %d ", ptr->key);
}
}
int main(void)
{
FILE *fp = fopen("input1.txt", "r");
FILE *fsearch = fopen("input2.txt", "r");
treePointer head = NULL;
int key;
while (!feof(fp))
{
fscanf(fp, "%d", &key);
insert(&head, key);
}
printf("Preorer: ");
preorder(head);
printf("\n");
printf("Inorder: ");
inorder(head);
printf("\n");
printf("PostOrder: ");
postorder(head);
printf("\n");
printf("Search: ");
int find;
while (!feof(fsearch))
{
fscanf(fsearch, "%d", &find);
if (iterSearch(head, find))
printf(" 1 ");
else
printf(" 0 ");
}
fclose(fp);
fclose(fsearch);
return 0;
}/input1.txt
30 5 2 40 80 35/input2.txt
1 2 40 90
여기에서 저희는 BST에 값을 하나하나씩 집어 넣었습니다. 집어 넣기 위해 저희는 modifiedSearch함수를 사용했습니다. 이는 만약에 tree가 null이면 NULL을 반환하고, 추가할 tree노드의 root를 반환하는 함수입니다. 아 그리고 만약 같은 값이 이미 있다면 NULL을 반환하게 코드를 작성해야 합니다.
이 modifiedSearch함수를 insert함수에서 사용합니다. 애초에 !(*node)가 없거나 temp가 있는 경우에만 실행되는데, *node가 있는 경우에는 modifiedSearch의 반환값에서 왼쪽 오른쪽만 잘 설정해서 삽입해주기만 하면 됩니다. 만약 아닌 경우(!(*node))인 경우는 *node자체를 삽입하고자 하는 배열로 박아주면 됩니다.
또한 while문으로 값을 찾을 수도 있습니다. root을 가리키는 tree Pointer부터 같으면 바로 tree를 반환해주면 되고 왼쪽 오른쪽으로 가다가 만약에 tree가 null인 동안 찾지 못하면 값이 없는거니까 NULL을 가리키게 해주면 됩니다.
Deletion
BST의 삭제는 크게 두 가지 경우가 존재합니다. 첫번째는 leaf node 즉, 자식이 없는 노드를 삭제하는 경우입니다. 두번재는 non-leaf node, 자식이 있는 노드를 삭제하는 경우입니다.
자식이 없는 노드를 삭제
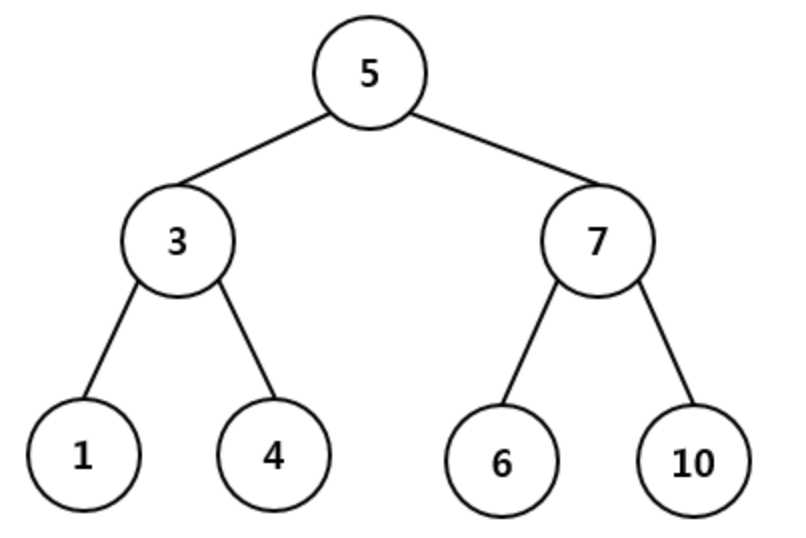
위와 같은 트리가 있다고 해 봅시다. 위의 트리에서 1, 4, 6, 10중 하나를 삭제 한다고 해 봅시다. 그럼 삭제 방법은 아주 간단합니다. 해당 노드를 그냥 null로 바꾸어 버리면 됩니다.
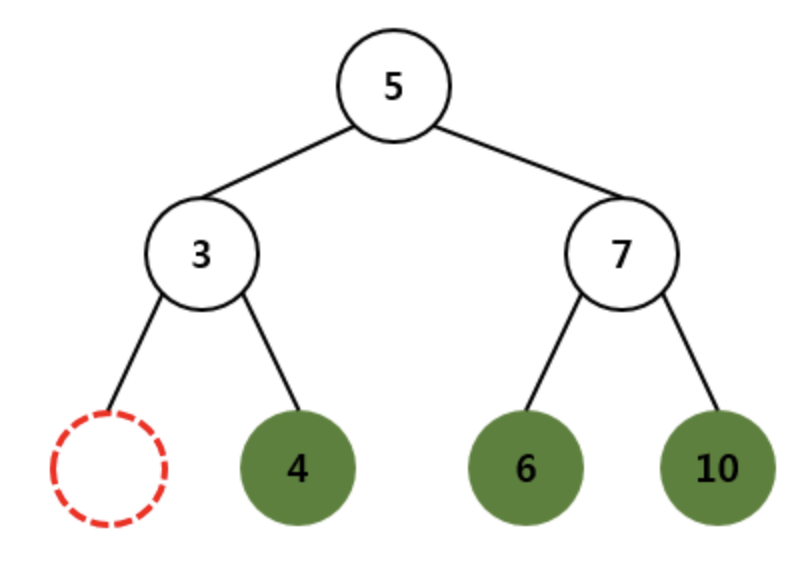
다음과 같은 형태로 BST가 바뀌게 될 것입니다.
자식이 있는 노드의 삭제
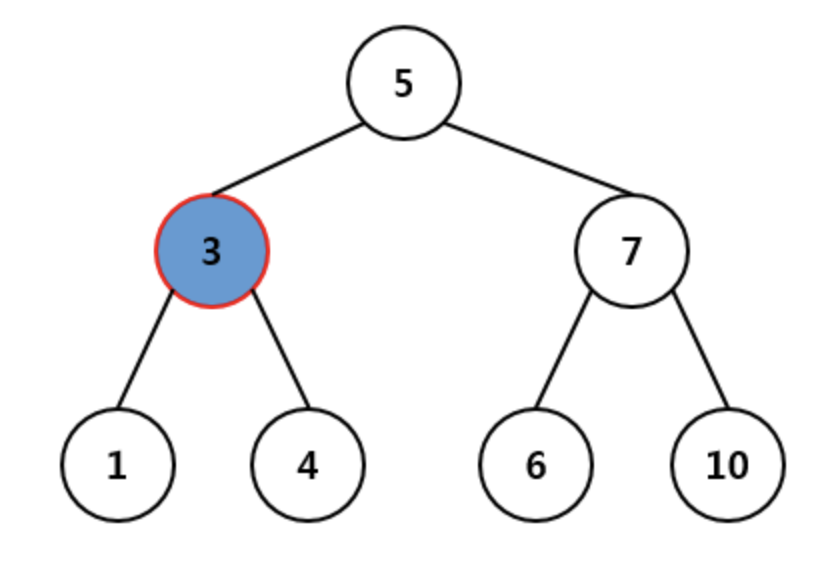
다음과 같은 트리가 있다고 해 봅시다. 위의 그림처럼 자식이 둘이나 있는 노드 3을 삭제한다고 해 봅시다. 3을 그대로 삭제해 버리면
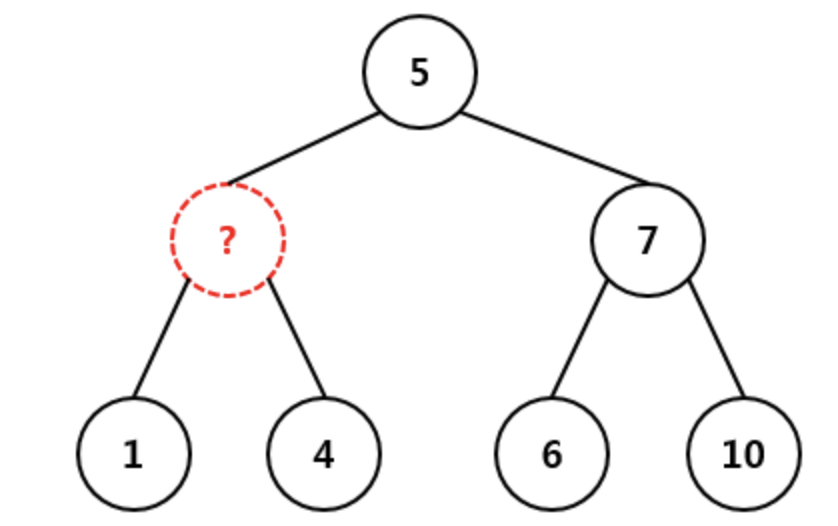
다음과 같이 1, 4는 아무것도 아닌게 됩니다. 따라서 자식이 있는 노드를 삭제하고 난 후에는 반드시 다른 노드를 부모로 만드는 일이 수행되어야 합니다. 여기서 부모가 될 수 있는 노드는, 왼쪽 서브 트리에서 가장 큰 노드와 오른쪽 서브 트리에서 가장 작은 노드입니다. 따라서 왼쪽 subtree에서 가장 작은 노드인 1이나 오른쪽 subtree에서 가장 큰 노드인 4 모두 부모로 만들어 주면 됩니다.
그리고 너무 쉬워서 뺄려고 생각했지만, 만약 자식이 1개인 경우도 그냥 자식이 없는 노드와 같이 삭제의 부모 노드를 그 삭제하려는 노드의 자식과 연결해 주면 됩니다.
Height of BST
만약에 [1, 2, 3, 4, ... ,n]을 트리에 차례대로 삽입한다고 하면, skewed binary search tree가 나오게 되어 높이가 n이 됩니다.
하지만 평균적으로 BST의 높이는 O(logN)이 됩니다. 최악의 경우에도 높이가 O(logN)이 된다면, 이를 balanced search tree라고 합니다. 이는 탐색, 추가등,.. 모든 작업을 O(h)로 수행합니다. h는 balanced search tree의 높이입니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Tree ( Forests ) (0) | 2022.05.31 |
|---|---|
| Data Structure - Tree ( Selection Tree ) (0) | 2022.05.31 |
| Data Structure - Tree ( Heaps ) (0) | 2022.05.31 |
| Data Structure - Hashing ( Dynamic Hashing ) (0) | 2022.05.30 |
| Data Structure - Hashing ( Overflow handling ) (0) | 2022.05.30 |
