Forests
forest란 n>=0인 disjoint tree들을 말합니다.
우리는 이러한 forest를 가지고 활용을 할 겁니다.

먼저 다음과 같이 S1 = {0, 6, 7, 8}, S2 = {1, 4, 9}, S3 = {2, 3, 5}이렇게 있다고 해 봅시다. 이 들은 모두 disjoint한 set들입니다.
만약에 Si와 Sj가 disjoint한 집합들이면, Si union Sj가 존재하게 됩니다. 만약 S1과S2를 합치게 되면 아래와 같은 두 그림이 될 수 있습니다.

Representation of Sets
우리는 이러한 집합들을 표현할 수 있는 방법을 정의해야 합니다. 우리는 root pointer가 각각의 set name에 해당하는 포인터를 가리키게 해야 합니다. 다음 과 같은 예시를 봅시다.

또한 우리는 각각의 노드의 숫자들을 인덱스로 활용할 수 있습니다. 그리고 각각의 필드들은 각각의 부모를 가리키고 이를 써주면 되고 root node들은 -1을 적어 주면 됩니다.

이러한 집합의 표기법을 알아보았는데, 이제는 각각의 집합에서 root를 찾는 simpleFind(), Set(i)를 Set(j로 갔다 붙이는 방법인 SimpleUnion()이 필요합니다. 이들은 아주 간단하게 구현이 가능합니다.

다음과 같이 반복문으로 -1이 안나올 때까지 돌려주다가 -1이 나왔을 때의 i값이 root이 되는 것이고, 합치는 것은 parent[i]를 j로 만들기만 하면 끝입니다.
Degenerate Tree
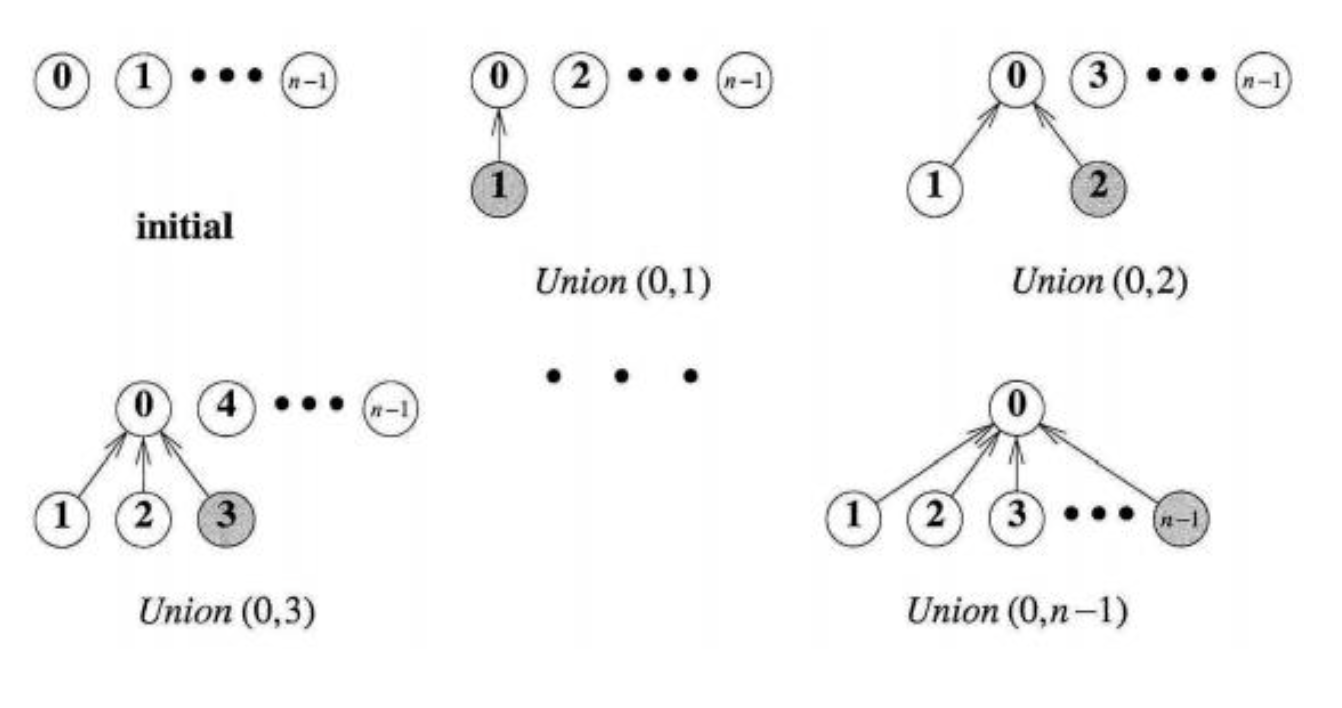
SimpleUnion()과 SimpleFind()는 구현하기 엄청 쉽습니다. 하지만 성능이 매우 좋지는 못합니다. 그 이유는 만약 예시를 들어 봅시다. Si = {i} 이고 0 <= i < p인데, 각각의 parent는 모두 다 -1인 상황입니다.그리고 우리는 union(0, 1), find(0) -> union(1, 2), find(0) -> ... -> union(n - 1, n - 1), find(0)을 하게 되면 우리는 degenerate tree를 만들게 됩니다.
simpleUnion()은 O(1)의 시간복잡도를 가지지만 n-1번의 union은 O(n)입니다. 또한 i level의 원소를 find하는 것은 O(i)가 소요되는데 둘을 합치면 2중 for문 이니까, O(n^2)가 됩니다.
이러한 degenerate tree를 만들지 않기 위해서 우리는 weighting rule을 union(i, j)를 사용하기 위해 제안합니다.
Weighting Rule
weighting rule은 제안합니다. Union(i, j)에서 i tree에 있는 node의 개수와 j tree에 있는 node의 개수 중 더 작은 것이 부모 노드가 되면 되겠다라고요, 그리고 이를 하기 위해 우리는 root의 값을 (-count)로 즉 개수의 음수로 나타내 주어야 합니다. 이에 대한 구현은 아래와 같습니다.

이에 대한 코드는 말한 그대로 입니다. temp로 각각의 parent의 값을 더한다음에, parent[i]와 parent[j]중 더 작은 값을 가지는 애를 새로운 부모로 만들어 주면 됩니다.
그리고 여기서 더 한단계 발전된 tree를 만들기 위해 Collapsing Rule을 사용합니다.
Collapsing Rule
먼저 그림부터 보시죠
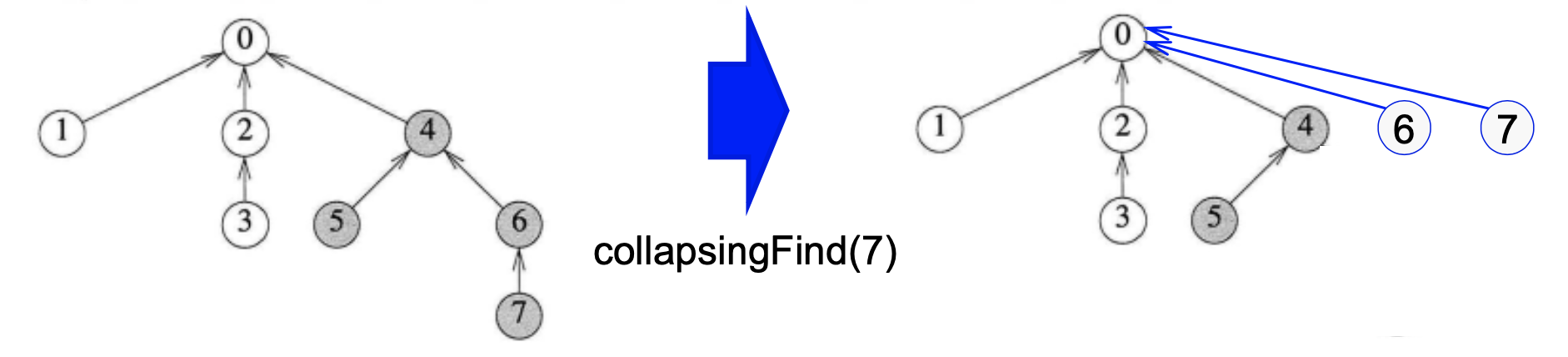
다음과 같이 트리가 있다 했을 때, CollapsingFind(7)을 하게 되면, 일단 부모 노드인 0을 찾게 되고, 부모 노드로 올라가면서 다 부모를 가리키게 바꾸어 주면 됩니다.
구현은 아래와 같습니다.
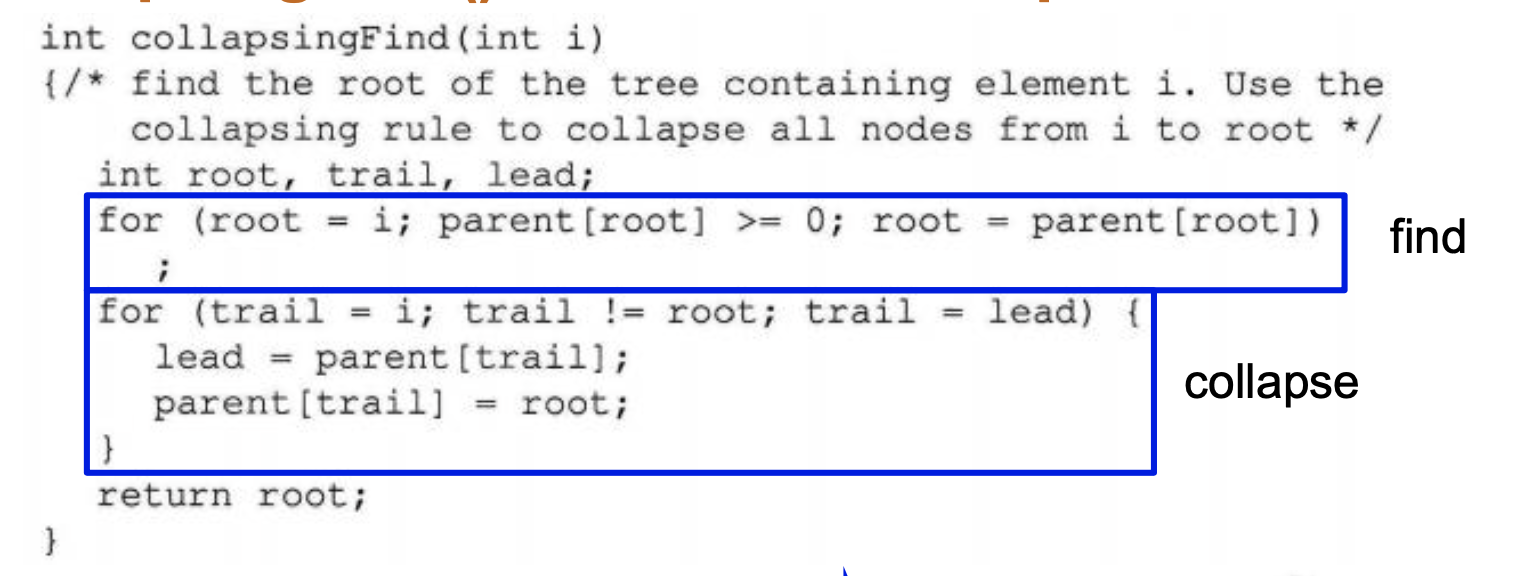
이제 이러한 개념들을 활용해서 Equivalence Classes에 적용해 보도록 하겠습니다.
Application to Equivalence Classes
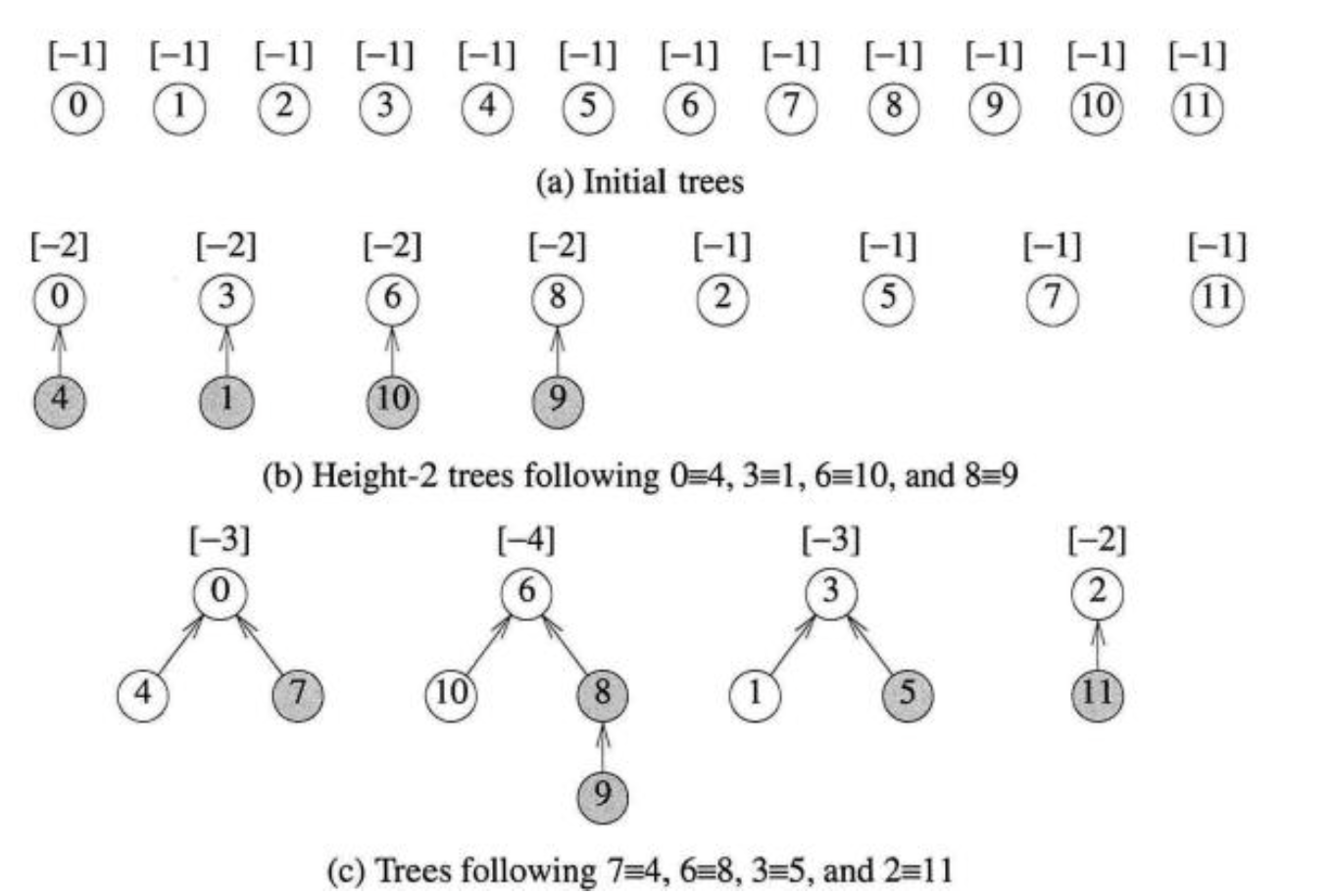
equivalence classes들의 연산들을 Union(i, j)으로 적용하고 나면 최종적으로 맨 아래와 같은 클래스가 나오게 되어, equivalence class를 구별하는데, 아주 쉬워집니다.
Counting Binary Tree
만약 n = 0, n =1이라면 우리는 단 한개의 binary tree를 만들 수 있습니다.
또한 만약 n = 2라면, 여기에는 서로 다른 2개의 binary tree가 있을 수 있습니다.
또한 n = 3이랴면, 5개가 존재하게 되죠 n = 3일 때의 binary tree의 개요는 아래와 같습니다.
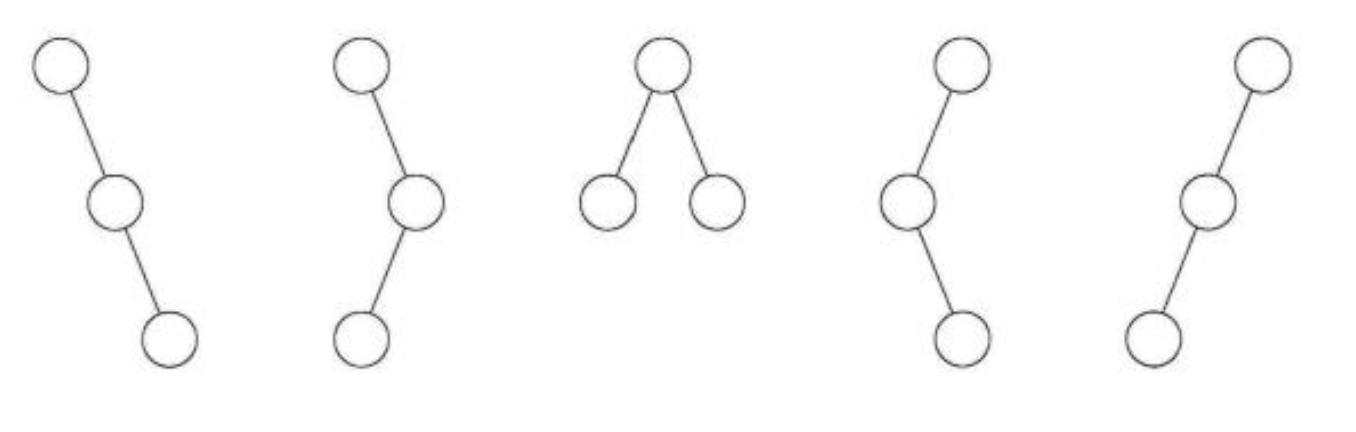
Stack Permutations
우리는 preorder sequence ABCDEFGHI와 inorder sequence BCAEDGHFI을 보고 트리를 그릴 수 있어야 합니다.
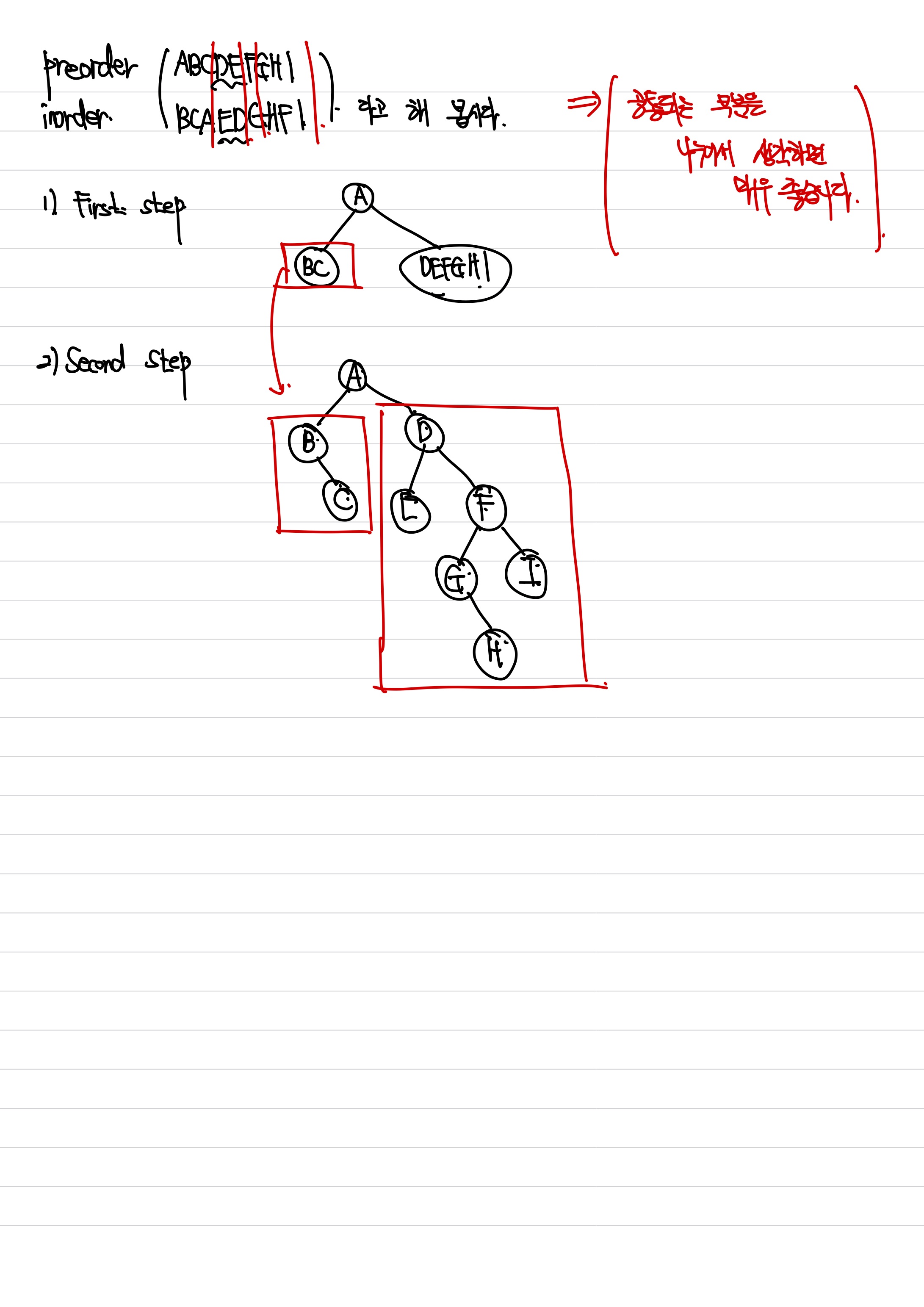
다음과 같이 최종 트리가 그려지게 됩니다. 이는 unique pair입니다. 단 하나의 binary tree가 존재한다는 것이지요. 저만의 팁을 드리자면 그냥 공통된 부분을 그려서 하나씩 매칭시켜주면 쉽습니다. ㅎㅎ
그리고 신기한 거 하나더 말씀드리겠습니다. stack에서 pop(), push()로 나올 수 있는 경우의 수와 그릴 수 있는 binary tree의 개수와 동일하다는 것입니다. n = 3일 때를 예시들어보겠습니다.

다음과 같이 stack에서 나오는 결과와 binary tree를 inorder traversal한 경우의 수 즉 그릴 수 있는 binary tree의 개수와 동일 하다는 것을 알 수 있습니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Graph ( DFS, BFS ) (0) | 2022.06.05 |
|---|---|
| Data Structure - Tree ( Selection Tree ) (0) | 2022.05.31 |
| Data Structure - Tree ( BST ) (0) | 2022.05.31 |
| Data Structure - Tree ( Heaps ) (0) | 2022.05.31 |
| Data Structure - Hashing ( Dynamic Hashing ) (0) | 2022.05.30 |
