Selection Tree
우리는 k개의 연속된 sequence가 있게 됩니다. 이를 우리는 runs라고 합니다.

이들은 모두 하나의 배열로 정렬되어 나올겁니다. 그리고 각각의 runs들은 오름차순으로 정렬되어 있습니다. 그리고 그 안의 값들을 key라고 합니다.
그리고 n을 우리는 이제부터 records의 개수로 정의할 수 있습니다. 그리고 위 runs sequence를 가지고 정렬을 하려면 merging task을 수행해 주어야 합니다. 반복적으로 가장 작은 키를 도출해 내면서 말이죠, 이 때 k - 1번의 비교가 필요하게 됩니다. 그리고 k > 2인 상황에서, 우리는 reduction작업을 통해 winner and loser tree를 구성해 낼 수 있게 됩니다.
Winner Trees
우리는 이를 승리 트리라고 합니다. 이는 complete binary tree로서 각각의 노드는 두개의 자식중에서 더 작은 노드를 말합니다.
- root node는 tree에서 가장 작은 노드를 가리킵니다.
- 이는 tournamet를 진행하면서 즉 아래부터 비교해 가면서 구축해 가집니다.
- 또한 각각의 leaf node는 각각의 run에 해당하는 first record를 가리킵니다.
- 그리고 이는 array representation으로 만들어 나갈 수 있습니다.

그리고 위 runs를 통해 이와 같은 첫번쨰 winner tree를 만들었다고 가정해 봅시다. 6을 빼고 winner tree를 재구축 하는데 필요한 시간 복잡도는 O(logk)가 됩니다. 그리고 n개의 record를 모두 다 합치는데에는 O(nlogk)가 들게 됩니다.
Loser Tree
selection tree중에 nonleaf node가 각각의 tournament에서 진 노드를 가리킨 트리를 우리는 loser tree라고 합니다.
그리고 추가적으로 winner tree와는 다르게 0번 인덱스가 추가 되었는데, 이는 최종적으로 이긴 노드를 써주기 위한 노드입니다. 여기에서 재구성을 해 줄 필요는 없습니다.

그리고 이를 재구성 할 때는 이의 형제들과 (11 -> 0)으로 가면서 비교할 필요가 없습니다.

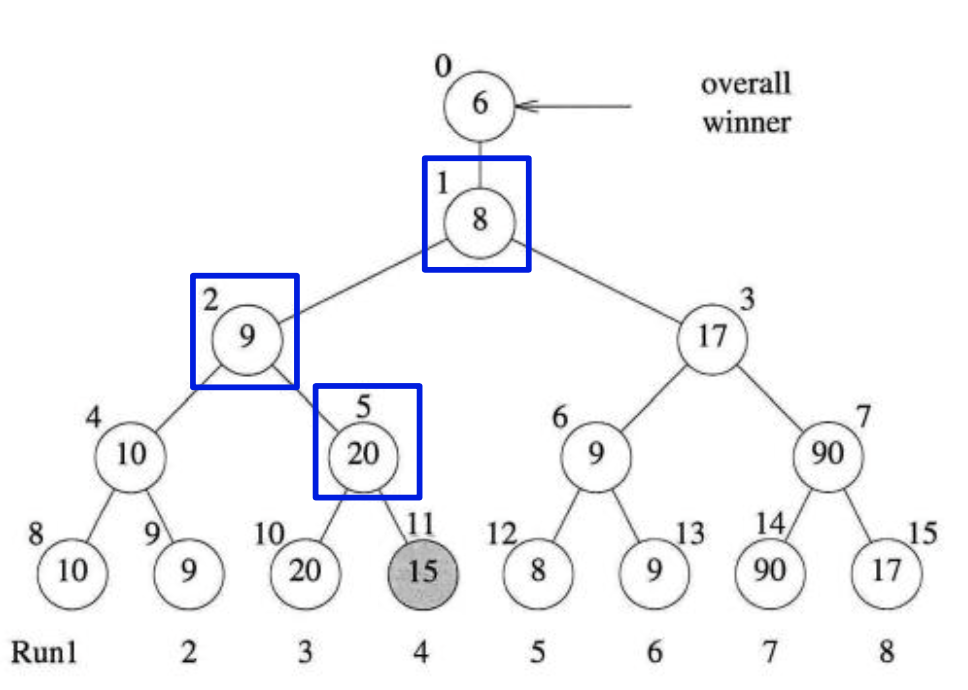
다음과 같이 상이하게 재구성하는 것을 보실 수 있습니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Graph ( DFS, BFS ) (0) | 2022.06.05 |
|---|---|
| Data Structure - Tree ( Forests ) (0) | 2022.05.31 |
| Data Structure - Tree ( BST ) (0) | 2022.05.31 |
| Data Structure - Tree ( Heaps ) (0) | 2022.05.31 |
| Data Structure - Hashing ( Dynamic Hashing ) (0) | 2022.05.30 |
