hash table에서 overflow는 새로운 사전에서 slot이 꽉찼을 떄 발생한다고 앞에서 말씀드렸습니다.
이를 다루기 위해서 두가지 방법을 소개합니다.
- Open addressiong
- Linear probing
- Quadratic probing
- Rehashing
- Random probing
- Chaining
Linear probing

우리가 key를 집어 넣을 떄, linear probing은 ( ht[h(k) + i] % b, 0 <= i <= b - 1 )이 순서대로 차례대로 검색을 합니다. 여기서 우리는 처음으로 채워지지 않은 bucket을 찾게 되면, 멈추게 되고, 여기에다가 그냥 값을 집어넣게 됩니다.
만약 어느 bucket도 찾지 못했다면, hash table이 꽉 찼다는 뜻이고, a ( loading factor )가 1을 넘었다는 뜻입니다. 우리는 이 때 table의 size를 증가 시켜주어야 합니다. 이러한 table의 size를 증가시켜주려면, 해시 함수를 바꾸어 주어야 하며, 이에 대한 key들을 적절한 값에 다시 재배치 해주어야 합니다.
이에 대한 절차를 꼼꼼히 서술해 보도록 하겠습니다.
- h(k)의 값을 계산합니다. (key를 해시 함수에 적용한 값)
- ht[h(k)], ht[(h(k) + 1) % b], ... ,ht[(h(k) + j) % b]을 반복해서 계산해 갑니다.
- ht[(h(k) + j)%b]에 해당하는 값이 비어져 있거나
- 만약 모든 순서를 반복하고 시작 지점으로 돌아와 테이블이 꽉 찼음을 알리면, ht[h(k)]을 반환합니다.
이를 코드로 간단히 구현해 보도록 하겠습니다.
/LinearProbing.c
#include <stdio.h> #include <stdlib.h> int hashFunction(int key, int tableSize) { return key % tableSize; } void structHashTable(int key, int tableSize, int *hashTable) { int hashValue = hashFunction(key, tableSize); for (; hashTable[hashValue]; hashValue++) ; hashTable[hashValue] = key; } int *search(int key, int tableSize, int *hashTable) { int homeBucket, currentBucket; // 들어온 key값에 대한 hashfunction의 값을 구합니다. homeBucket = hashFunction(key, tableSize); for (currentBucket = homeBucket; hashTable[currentBucket] && hashTable[currentBucket] != key;) { currentBucket = (currentBucket + 1) % tableSize; if (currentBucket == homeBucket) return NULL; } if (hashTable[currentBucket] == key) return &hashTable[currentBucket]; return NULL; } int main(void) { FILE *fp_read = fopen("input.txt", "r"); int dataNum, tableSize; int *hashTable; if (fp_read == NULL) { fprintf(stderr, "File Open Error!"); exit(EXIT_FAILURE); } int SearchNum; fscanf(fp_read, "%d", &tableSize); fscanf(fp_read, "%d", &dataNum); fscanf(fp_read, "%d", &SearchNum); hashTable = (int *)malloc(sizeof(int) * tableSize); int temp; for (int i = 0; i < dataNum; i++) { fscanf(fp_read, "%d", &temp); structHashTable(temp, tableSize, hashTable); } printf("Hash Table: \n"); for (int i = 0; i < tableSize; i++) { if (hashTable[i] == 0) printf("%d: \n", i); else printf("%d: %d\n", i, hashTable[i]); } int searchNum; printf("Search: \n"); for (int i = 0; i < SearchNum; i++) { fscanf(fp_read, "%d", &searchNum); search(searchNum, tableSize, hashTable) != NULL ? printf("S") : printf("F"); } return 0; } //Hash Table: //0: //1: 91 //2: 2 //3: 41 //4: //5: 15 //6: //7: //8: 8 //9: 88 //Search: //FSS%
/input.txt
10 6 3 8 15 91 2 88 41 4 41 15
우선 tableSize, dataNumber, SearchNum즉, 테이블의 크기와, 데이터를 얼마나 받을건가, 그리고 몇개를 찾아볼 건가를 미리 받아 놓습니다.
그리고 collision이 일어나게 되면, 그 아래로 쭉쭉 빈 칸을 찾아서 값을 집어 넣습니다. 그리고 찾을 때는 위에서 설명한 linear probing기법을 사용해서 찾아냈습니다.
이에 대한 조금 예시를 하나 더 들어보겠습니다
예시 2
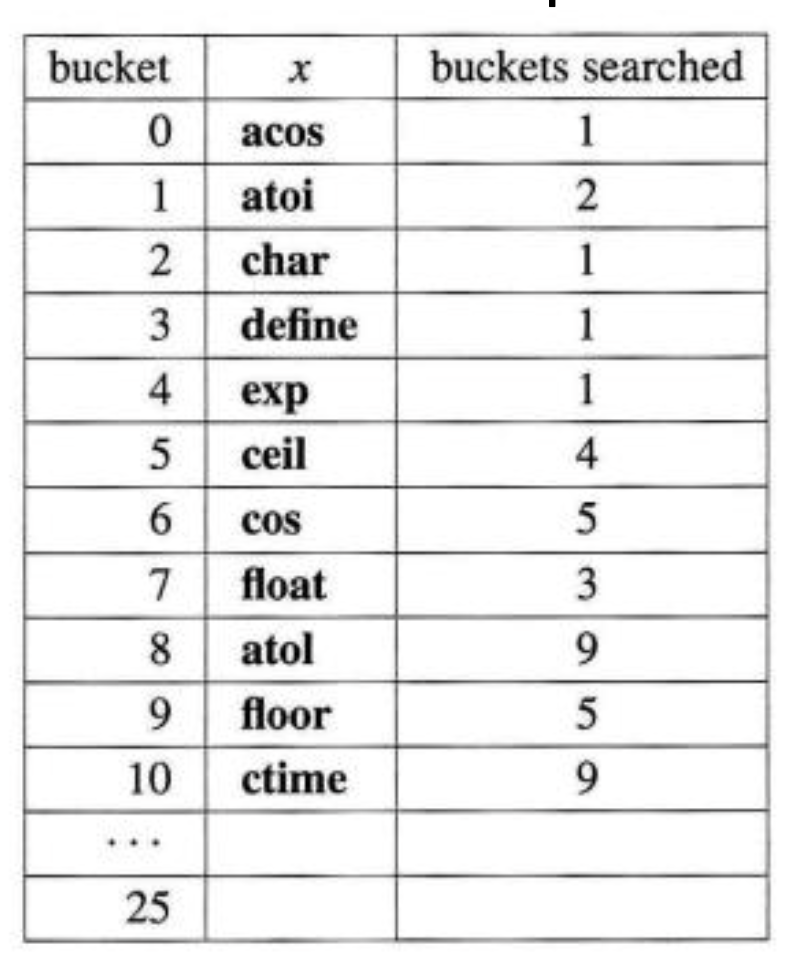
b = 26, s = 1, data = (acos, atoi, char, define, exp, ceil, cos, float, atol, floor, ctime)이 있다고 해 봅시다. 이 떄의 hash function은 문자열의 첫번쨰 값이라고 합시다. 이 떄 우리가 atol을 삽입하기 위해서는 ht[0],...ht[8]까지 총 9번을 비교해야 합니다. 위의 표에 보시면 각각의 값이 삽입될 때 몇번 비교되어 찾아졌는지 나와있습니다. 이를 다 더한다음에 개수로 나누어 보면 41/11 = 3.72가 나오는데, 꽤 높은값 이 나오는 것을 볼 수 있습니다.
이에 대한 uniform hash function에서의 평균적인 key가 comparison되는 갯수를 통계내어 봤더니 대략 (2-a)/(2-2a)가 나옴을 볼 수 있었습니다. ( 이 떄 a는 loading factor )입니다. 이 상황에서 위 값을 구해보면, a = n/(sb) = 11/26 = 0.42이 됨을 확인할 수 있습니다. 그리고 위의 값을 p라고 하면 (2-0.42)/(2-2*0.42) = 1.36이 나옴을 확인할 수 있습니다. 위의 11개만 계산해 본 값보다 작지만, 최악의 경우 즉 Worst Case는 꾀나 클 수 있습니다.
Quadratic Probing
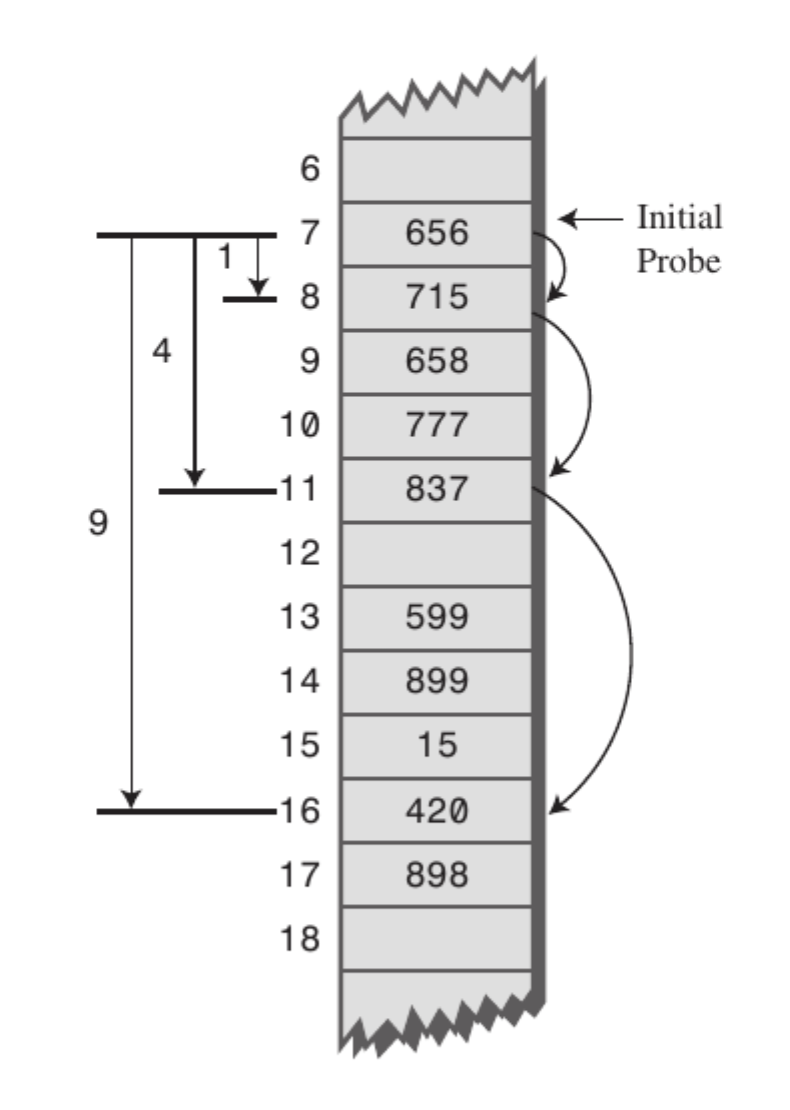
제곱 탐사(Quadratic probing)은 고정 폭으로 이동하는 선형 탐사와 달리 그 폭이 제곱수로 늘어난다는 특징이 있습니다. 예컨대 임의의 키 값에 해당하는 데이터 엑세스할 때 충돌이 일어나면 1^2칸을 옮깁니다. 여기에서도 충돌이 일어나면 이번엔 2^2칸, 그 다음엔 3^2칸 옮기는 식입니다.
하지만 제곱탐사는 여러 개의 서로 다른 키들이 동일한 초기 해시값을 갖는 secondary clustering에 취약합니다. 초기 해시값이 같으면 다음 탐사 위치 또한 동일하기 때문에 성큼성큼 이동하더라도 탐사를 네 번 수행하고 나서야 비로소 데이터를 저장할 수 있기 때문입니다.
이 외에도 Random Probing이라는 기법이 있습니다.
Chaining
해시충돌 문제를 해결하기 위한 간단한 아이디어 가운데 하나는 한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 것입니다. 해당 버킷에 데이터가 이미 있다면 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현(연결리스트)하기 때문에 체인이라는 말이 붙은 것 같습니다. 유연하다는 장점을 가지나 메모리 문제를 야기할 수 있습니다.
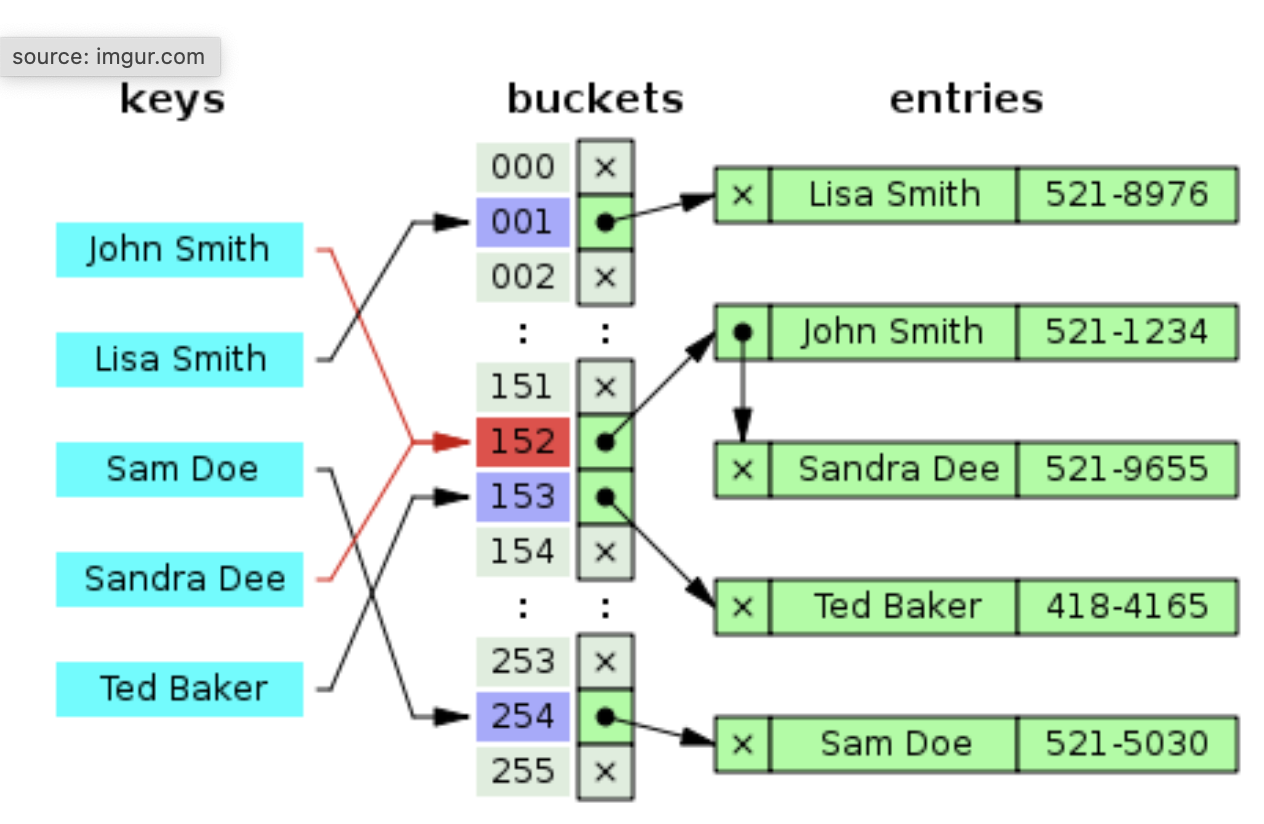
위 예시 그림의 해시 함수는 'John Smith'와 'Sandra Dee'를 같은 해시값(152)으로 매핑하고 있습니다. 이 경우 해당 해시값에 대응하는 동일한 버킷에 두 개 데이터를 저장해 둡니다. 데이터를 위 그림처럼 연결리스트로 저장해 둘 경우 최근 데이터는 연결리스트의 head에 추가됩니다. ( 이 경우 O(1), tail에 저장할 경우 O(n)이 됨)
삽입, 탐색, 삭제 연산과 계산복잡성
chaining 방식의 계산 복잡성을 따져보겠습니다, 해시 테이블의 크기가 m, 실제 사용하는 키 개수가 n, 해시 함수가 키들을 모든 버킷에 균등하게 할당한다고 가정하면, 버킷 하나당 n/m = a개의 키들이 존재할 것입니다. 예컨데 위 그림 예시에서 2560개의 키에 해당하는 데이터를 저장한다면 버킷 하나당 10개의 데이터가 있다는 얘기입니다.
삽입
위 예시그림의 해시함수가 254로 매핑하는 'Mark Zuckerberg'의 전화번호를 새로 추가한다고 칩시다. 'Mark Zuckerberg'라는 키를 해시값 254로 매핑하는 데 O(1)이 듭니다. 해당 해시값에 해당하는 연결리스트의 head에 이를 추가하는 데 O(1)이 듭니다. 따라서 삽입의 계산 복잡성은 둘을 합친 O(1)입니다.
탐색
쿼리 키값에 해당하는 데이터가 해시테이블에 존재하지 않는 경우입니다. 예컨데 위 예시 그림의 해시함수가 152로 매핑하는 'Steve Jobs'의 전화번호를 탐색한다고 가정해 봅시다. 이 경우 키를 해시값으로 바꾸고, 해당 해시값에 해당하는 버킷의 요소들 a개를 모두 탐색해 봐야 존재하지 않는다는 사실을 알 수 있습니다. 따라서 이 경우 계산 복잡성은 O(1 + a)이 됩니다.
Big O notation의 계산복잡성을 따져보기 위해선 최악의 경우를 고려해야 합니다. 해당 버킷의 tail에 값이 있는 경우일 겁니다. 데이터가 해시테이블에 존재한다고 가정했으므로 버킷 내 a개 요소 가운데 반드시 찾고자 하는 값이 존재합니다. a-1개를 비교했는데도 원하는 값을 찾지 못했다면 tail값은 따져볼 필요도 없이 찾고자 하는 값이 됩니다.
그런데 버킷의 요소들 평균이 a개일 때 successful search는, 요소가 a - 1개인 버킷을 탐색했는데 찾는 값이 없어서, 해당 버킷에 쿼리에 해당하는 데이터를 삽입하여 결과적으로 해당 버킷의 요소 수를 a개로 만드는 계산량과 동일합니다. 즉 O(1 + a)이 됩니다.
삭제
탐색과 본질적으로 비슷합니다. 우선 쿼리 키값을 해시값으로 매핑하고(O(1)), 해당 버킷 내에 키값에 해당하는 데이터가 있는지 탐색(O(a))해야 합니다. 물론 탐색 연산에 비교해 삭제에 드는 계산도 추가적으로 필요하나, 연결리스트로 해시테이블을 구현할 경우 삭제 연산의 계산 복잡성은 O(1)이므로 무시할 만한 수준이 됩니다.
chaining에서 삽입을 제외한, 탐색/삭제의 계산복잡성은 버킷당 요소 개수의 평균 a가 좌지우하는 구조입니다. 최악의 경우 한 버킷에 모든 데이터가 들어 있어 O(n)이 될 수 있습니다. 하지만 데이터의 개수가 해시테이블 크기의 두 세베쯤(a = 2 ~ 3)만 되어도, 탐색, 삭제는 O(1)이 됩니다.
예시
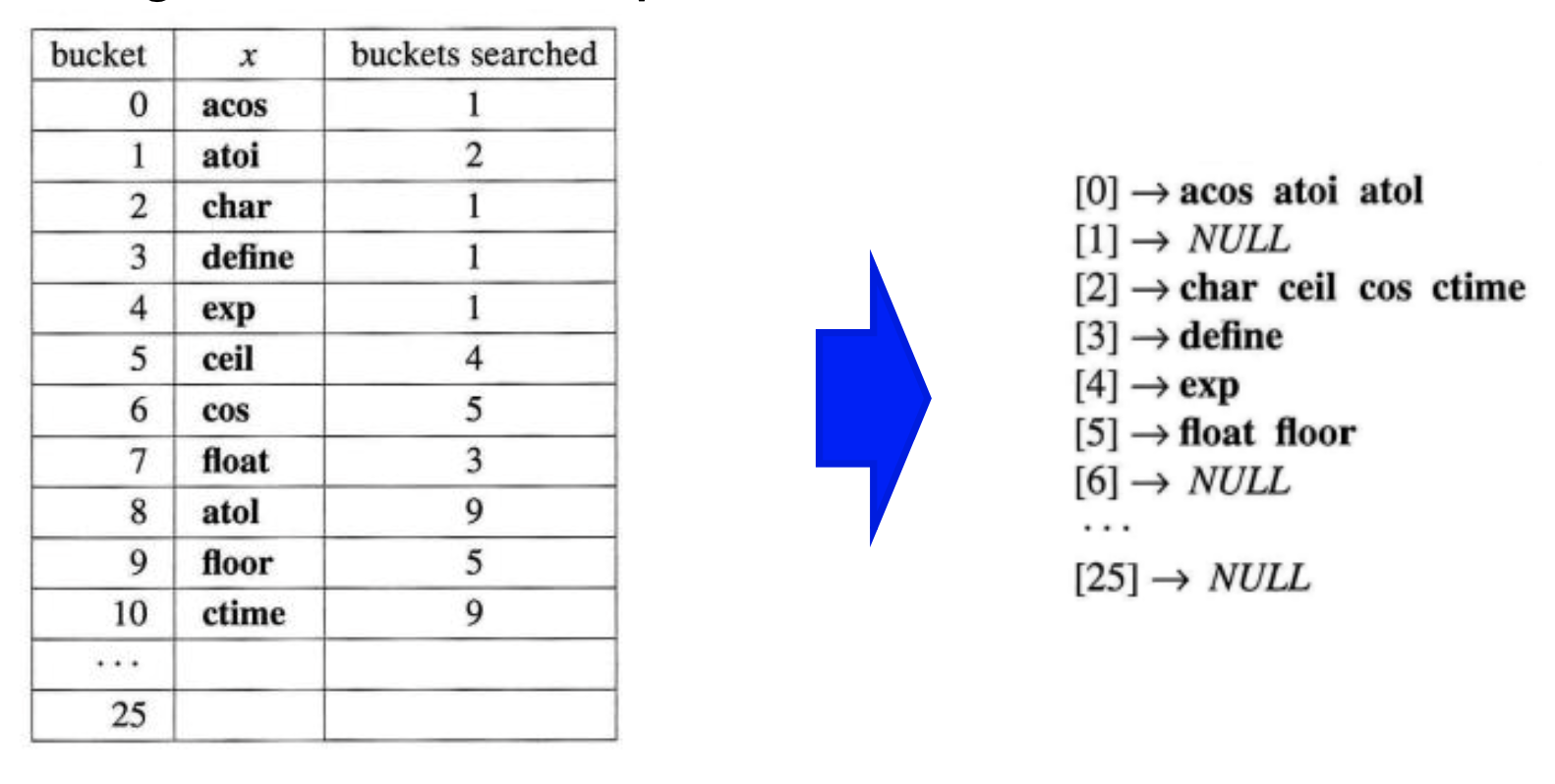
다음과 같이 위에서 linear probing했던 예시를 linked-list를 사용하여 chaining으로 바꾸어 보았습니다. 여기에서 평균 비굣값을 구해보면 21 / 11으로 1.91이 나오는데, linear probing을 했을 떄 나왔던 3.72보다 훨씬 낮은 값을 확인할 수 있습니다.
여기에서 통계학적으로 평균적으로 1 + a/2의 평균 비교 횟수가 나오는데, loading factor는 11/26 = 0.42 -> p = 1 + 0.42/2 = 1.21가 나오게 됩니다.
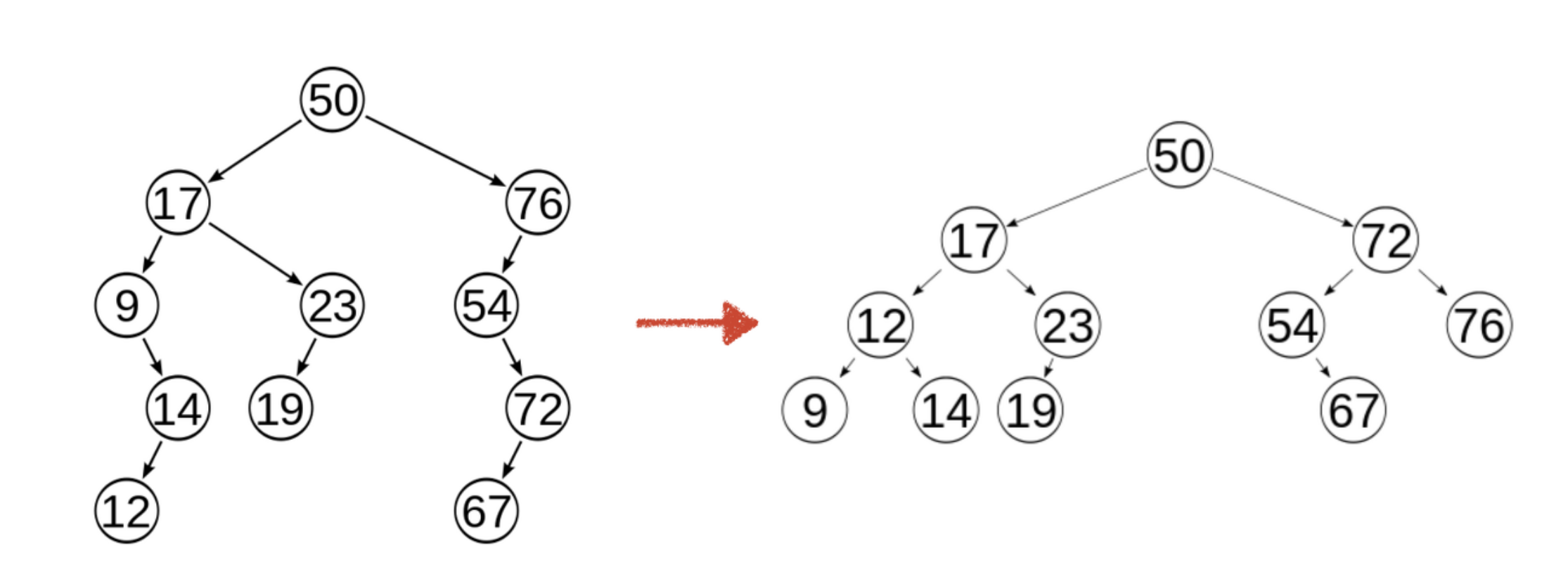
또한 위에서 살펴본 것처럼 하나의 key에 모두 다 쳐 박아 놓는 경우 계산 복잡도는 O(n)이 되게 됩니다. ( open addressing이나 chaining 모두 다 ) 여기에서 우리는 synonyms을 balanced search tree로 구축하게 되면 이는 O(logN)으로 줄게 됩니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Tree ( Heaps ) (0) | 2022.05.31 |
|---|---|
| Data Structure - Hashing ( Dynamic Hashing ) (0) | 2022.05.30 |
| Data Structure - Hashing ( Hash Functions ) (0) | 2022.05.29 |
| Data Structure - Hashing ( Introduce ) (0) | 2022.05.29 |
| Data Structure - Sorting ( Bubble, Selection Sort ) (0) | 2022.05.29 |
