How Fast Can We Sort
key에 의존한 comparisons와 interchanges가 있는 한 우리는 O(nlogn)보다 빠른 sorting algorithm을 만들 수 없습니다.

다음과 같이 decision tree를 그려서 input sequence R1, R2, R3에서 나올 수 있는 경우 의 수를 찾아보니 3!개가 나옵니다.
Theorm : Any decision tree that sorts n distinct elements has a height of at least log2(n!) + 1
- 우리가 n개의 원소를 정렬한다고 했을 때, 여기에서는 위에서 본 것처럼 n!개의 가능한 결과들이 있습니다. -> n1개의 leaft nodes가 존재하기 떄문
- 그리고 binary tree는 최대 2^(k-1)개의 leaves node를 가질 수 있습니다. ( 트리의 높이가 k )일 때
- 그러므로 높이는 무조건 적어도 log2(n!) + 1개 여야 합니다.
Corollary: Any algorithm that sorts only by comparisions must have at least computing time of omega(nlogn)
- tree의 height가 log2(n!) + 1입니다.
- n! >= (n/2)^(n/2)
- 그러므로 log2(n!) + 1 >= (n/2)log2(n/2) = omega(nlogn)
즉 최소한 sorting algorithm의 복잡도는 nlogn이여야 합니다.
Merge Sort
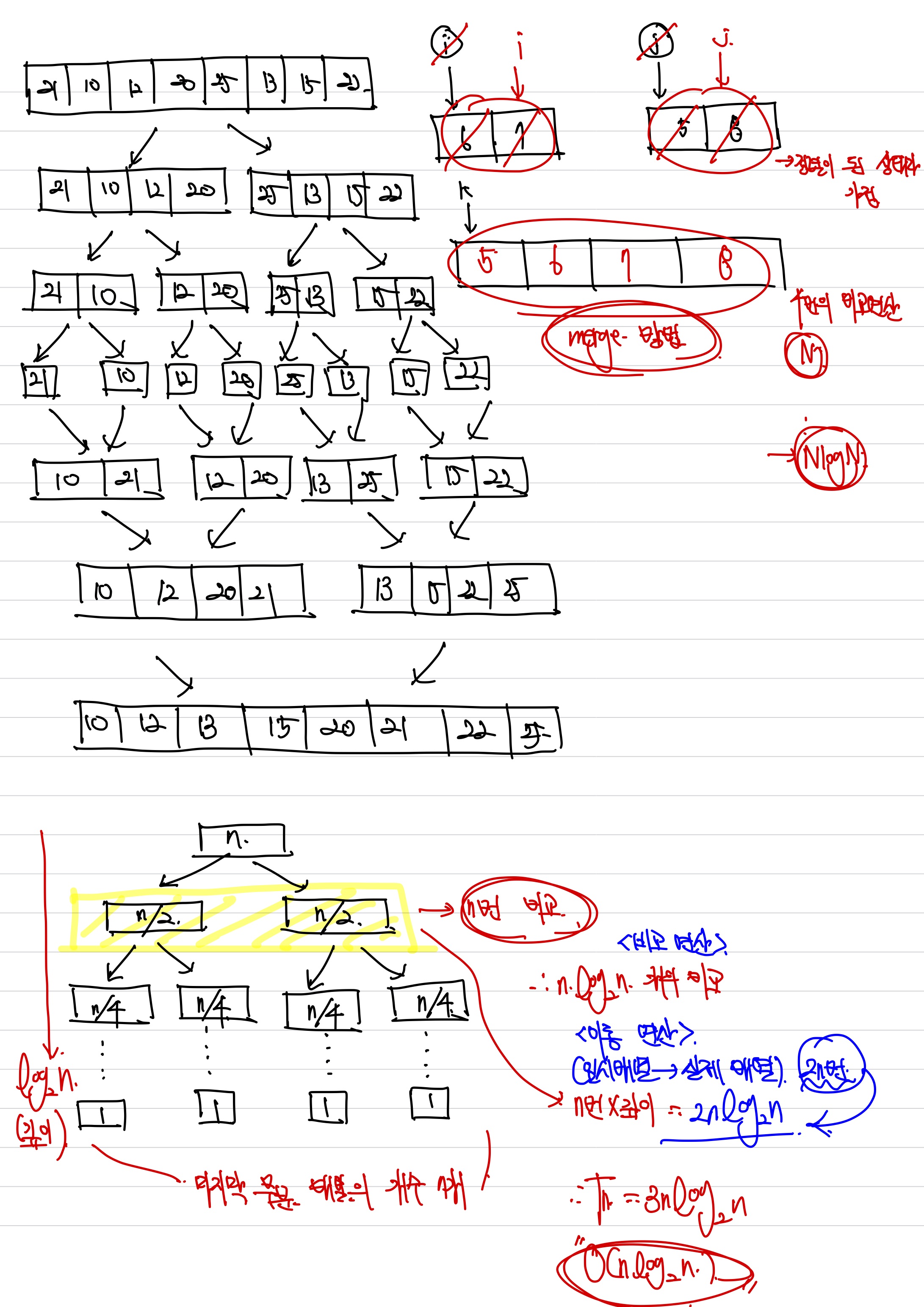
합병 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘 중 하나입니다.
이제 간단한 합병 정렬의 과정을 설명해 보도록 하겠습니다.
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 봅니다. 그렇지 않은 경우에는
- 정렬되지 않은 리스트를 절반으로 잘라서 비슷한 크기의 두 부분 리스트로 나눕니다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬합니다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병합니다.
/merge_sort.c
#include <stdio.h> #include <stdlib.h> #include <string.h> #define ARR_SIZE 100 int sorted[ARR_SIZE]; int seqSearch(int a[], int k, int n) { int i; for (i = 1; i < n && a[i] != k; i++) ; if (i >= n) return -1; return i; } int swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } void insertionSort(int a[], int n) { /* sort a[0:n - 1] into nondecreasing order( 오름 차순 ) */ int i, j, key; for (i = 1; i < n; i++) { key = a[i]; // 현재 정렬된 배열은 i - 1까지 이므로 i - 1번째부터 역순으로 조사합니다. for (j = i - 1; j >= 0 && a[j] > key; j--) a[j + 1] = a[j]; a[j + 1] = key; } } int partition(int list[], int left, int right) { int pivot; int low, high; low = left; high = right + 1; pivot = list[left]; // 정렬할 리스트의 가장 왼쪽 데이터를 피벗으로 선택 ( 임의의 값을 피벗으로 선택 ) /* low와 high가 교차할 때까지 반복 (low < high) */ do { /* list[low]가 피벗보다 작으면 계속 low를 증가 시켜줘야 한다. */ do { low++; } while (list[low] < pivot && low <= right); // low가 만약에 right이 된다면 멈처 주어야 합니다. do { high--; } while (list[high] > pivot && high >= left); // 만약 low와 high가 교차하지 않았으면 list[low]를 list[high]와 교환 if (low < high) swap(list + low, list + high); } while (low < high); // low와 high가 교차했으면 반복문을 빠져나와 list[left]와 list[high]을 교환해줘야 한다. swap(list + left, list + high); // 피벗의 위치인 high를 반환해주어야 합니다. return high; } void quick_sort(int list[], int left, int right) { /* 정렬할 범위가 2개 이상의 데이터가렴( 리스트의 크기가 0이나 1이 아니라면) */ if (left < right) { // partition함수를 호출하여 피벗을 기준으로 리스트를 비균등 분할 - 분할(Divide) int q = partition(list, left, right); // 피벗을 제외한 2개의 부분 리스트를 대상으로 순환 호출 quick_sort(list, left, q - 1); // (left ~ 피벗 바로 앞) 앞쪽 부분 리스트 정렬 - 정복(Conquer) quick_sort(list, q + 1, right); // (피벗 바로 뒤 ~ right) 뒤쪽 부분 리스트 정렬 - 정복(Conquer) } } void merge(int list[], int left, int mid, int right) { int i, j, k, l; i = left; j = mid + 1; k = left; /* 분할 정렬된 list의 합병 */ while (i <= mid && j <= right) { if (list[i] <= list[j]) sorted[k++] = list[i++]; else sorted[k++] = list[j++]; } // 남아 있는 값들을 일괄 복사 if (i > mid) for (l = j; j <= right; j++) sorted[k++] = list[j]; else for (l = i; i <= mid; i++) sorted[k++] = list[l]; for (l = left; l <= right; l++) list[l] = sorted[l]; } void merge_sort(int list[], int left, int right) { int mid; // 원소가 1개가 아닌 경우 if (left < right) { mid = (left + right) / 2; // 중간 위치를 계산하여 리스트를 균등 분할 - 분할(Divide) merge_sort(list, left, mid); // 앞쪽 부분 리스트 정렬 - 정복(Conquer) merge_sort(list, mid + 1, right); // 뒤쪽 부분 리스트 정렬 - 정복(Conquer) merge(list, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 - 결합(Combine) } else { // 원소가 1개라면 그냥 return시켜 주면 된다. return; } } void printArr(int a[], int n) { for (int i = 0; i < n; i++) printf("%d ", a[i]); putchar('\n'); } int main(void) { int sortArr[ARR_SIZE] = {0}; int count = 0; FILE *fp_read = fopen("sort.txt", "r"); while ((fscanf(fp_read, "%d", sortArr + count) != EOF)) { count++; } printf("original array: "); printArr(sortArr, count); // printf("[ 4 ] is in index %d\n", seqSearch(sortArr, 4, count)); int sortArr_2[ARR_SIZE]; memcpy(sortArr_2, sortArr, sizeof(int) * ARR_SIZE); printf("insertion sort: "); insertionSort(sortArr_2, count); printArr(sortArr_2, count); int sortArr_3[ARR_SIZE]; memcpy(sortArr_3, sortArr, sizeof(int) * ARR_SIZE); printf("quiuck sort:\t"); quick_sort(sortArr_3, 0, count - 1); printArr(sortArr_3, count); int sortArr_4[ARR_SIZE]; memcpy(sortArr_4, sortArr, sizeof(int) * ARR_SIZE); printf("merge sort:\t"); merge_sort(sortArr_4, 0, count - 1); printArr(sortArr_4, count); return 0; } // original array: 3 2 4 1 9 8 // insertion sort: 1 2 3 4 8 9 // quiuck sort: 1 2 3 4 8 9 // merge sort: 1 2 3 4 8 9
- 단점
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요합니다.
- 제자리 정렬(in-place sorting)이 아닙니다.
- 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므 매우 큰 시간적 낭비를 초래합니다.
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요합니다.
- 장점
- 안정적인 정렬 방법입니다.
- 데이터의 분포에 영향을 quick sort보다 덜 받게 됩니다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하게 됩니다.
- 만약 레코드를 연결 리스트(Linked-list)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아지게 됩니다.
- 따라서 제자리 정렬(in-place sorting)으로도 구현할 수 있게 됩니다.
- 따라서 크기가 큰 레코드를 정렬할 경우 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 정렬 방법보다 효율적입니다.
- 안정적인 정렬 방법입니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Sorting ( Several Keys && Radix Sort && External Sort ) (0) | 2022.05.28 |
|---|---|
| Data Structure - Sorting ( Heap Sort ) (0) | 2022.05.28 |
| Data Structure - Sorting ( Quick Sort ) (0) | 2022.05.28 |
| Data Structure - Sorting ( Insertion Sort ) (0) | 2022.05.28 |
| Data Structure - Graph ( AOV, AOE Network ) (0) | 2022.05.27 |
