AOV Network
AOV는 Activity On Vertex의 약자입니다. 즉 정점이 Activity 작업을 나타내고, 간선이 작업간의 우선순위 관계를 나타내는 방향 그래프입니다.

위의 그래프의 각 정점이 작업을 나타내다고 해 봅시다. 1번 작업이 끝나면 3, 4번 작업을 할 수 있고, 3, 4번 작업이 끝나야 5번 작업을 할 수 있고, 2번 작업이 끝나야 6번 작업을 할 수 있고, 마지막으로 5, 6번 작업이 끝나면 7번을 할 수 있는 식입니다.
predecessor는 어떤 작업을 하기 전에 해야하는 작업을 의미하고, successor는 어떤 작업을 하고 나서 해야 할 작업을 의미합니다. 앞에 immediate가 붙으면 바로 전, 바로 후의 작업을 의미합니다.
AOV네트워크에서 중요한 것은 어떤 순서로 일을 끝낼 것이냐? 입니다. 이를 위해 Topological sort라는 것이 존재합니다. BFS또는 DFS를 이용하여 구현할 수 있습니다.

위 그림에서의 위 개념을 정해 보도록 하겠습니다.
- C3과 C6은 C7의 immediate predecessor이라고 할 수 있습니다.
- C9, C10, C12, C13은 C7의 immediate successor라고 할 수 있습니다.
- C14는 C3의 successor이지만 immediate success라고 할 순 없습니다.
그리고 Topological orders를 찾는 방법을 알아보도록 하겠습니다.
- 첫번째로 predecessor가 없는 vertex를 찾습니다.
- 그리고 위에서 찾은 vertex를 이와 연결되어 있는 edge와 함꼐 삭제 합니다.

위의 예시를 적용해 보면 위 그래프의 topological orders는 0, 3, 2, 5, 1, 4가 될 수 있습니다. 이 외에도 더 많은 topological orders가 존재할 수 있습니다.
/AOV.c
#include <stdio.h> #include <string.h> #include <stdlib.h> #define MAX_VERTICES 100 typedef struct node_ { int vertex; struct node_ *link; } node, *nodePointer; typedef struct hdnodes { int count; nodePointer link; } hdnodes; hdnodes graph[MAX_VERTICES]; void topSort(hdnodes graph[], int n) { int i, j, k, top; nodePointer ptr; top = -1; for (i = 0; i < n; i++) { // graph[i].count의 값이 0이면 predecessor가 없는 것이므로 // i의 count를 -1로 하고 top의 값을 i로 한다. if (!graph[i].count) { graph[i].count = top; top = i; } } for (i = 0; i < n; i++) { // 만약 top if (top == -1) { fprintf(stderr, "\nNetwork has a cycle. Sort terminated. \n"); exit(EXIT_FAILURE); } else { j = top; top = graph[top].count; printf("%3d", j); for (ptr = graph[i].link; ptr; ptr = ptr->link) { k = ptr->vertex; graph[k].count--; if (!graph[k].count) { graph[k].count = top; top = k; } } } } } int main(void) { FILE *fp_read = fopen("input.txt", "r"); if (fp_read == NULL) { fprintf(stderr, "File Open Error!"); exit(EXIT_FAILURE); } int vertexNum; fscanf(fp_read, "%d", &vertexNum); int **input = malloc(sizeof(int *) * vertexNum); for (int i = 0; i < vertexNum; i++) input[i] = malloc(sizeof(int) * vertexNum); int num; for (int i = 0; i < vertexNum; i++) for (int j = 0; j < vertexNum; j++) fscanf(fp_read, "%d", &input[i][j]); nodePointer tempNode; nodePointer tempNode2; for (int i = 0; i < vertexNum; i++) { graph[i].link = NULL; for (int j = 0; j < vertexNum; j++) { if (input[i][j] != 0) { tempNode = malloc(sizeof(*tempNode)); tempNode->vertex = j; tempNode->link = NULL; // 현재 링크에 아무것도 없는 경우 if (!graph[i].link) { graph[i].link = tempNode; tempNode2 = tempNode; } else { tempNode2->link = tempNode; tempNode2 = tempNode; } graph[j].count++; } } } topSort(graph, vertexNum); return 0; }
/input.txt
6 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0
코드는 정확히 이해하지는 못햇으나 그냥
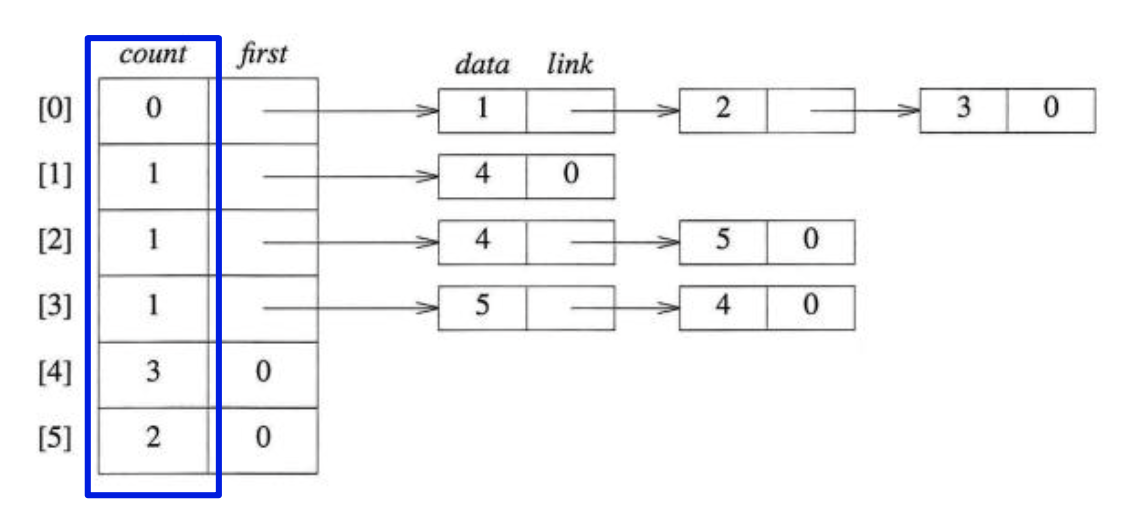
이런 식의 자료구조에서, indegree가 count인데, count가 0이라는 것은 predecessor가 없다는 뜻이고 이는 이제 이 vertex차례라는 것을 의미합니다. 그리고 0을 출력하고 없애면 이에 연결되어 있는 link vertex들에 해당하는 count를 그만큼 삭감 해주는 것이다. 그리고 또 0이 나오는 것이 있을 것이고 차례대로 또 위 과정을 반복하면 되는 것 같습니다.
AOE Network
AOE는 Activity On Edge의 약자로, 간선은 작업에 걸리는 시간을 가지고 있습니다. AOE 네트워크의 목표는 작업들을 수행하는 데 걸리는 최단시간을 구하는 것입니다.
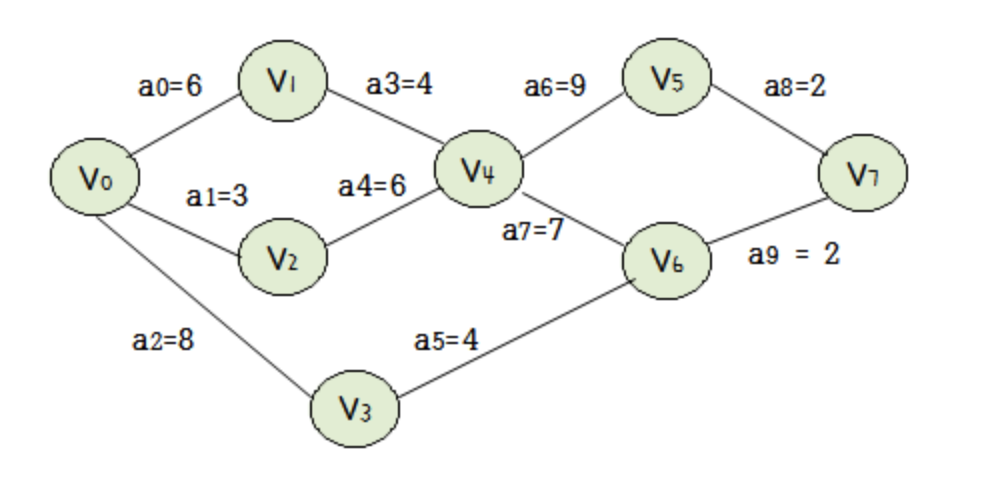
위의 그래프에서 V0가 시작점, V7이 도착점을 나타내게 됩니다.
AOE는 헷갈리는 용어가 많습니다.
# 정점 i, j가 있고, <i, j>를 나타내는 간선 k가 있을 때
early[k]는 간선 k가 실행되기 위한 가장 빠른 시간을 나타냅니다.
earlist[k]는 정점 i가 일어날 수 있는 가장 빠른 시간을 나타내게 됩니다.
예를 들어, 위 그래프에서 V4를 봅시다. V0 -> V1 -> V4를 거쳐 오는 경로는 "10"의 시간이 걸리고, V0 -> V2 -> V4를 거쳐 오는 경로는 "9"의 시간이 걸리게 됩니다. V1, V2이 모두 완료되어야 V4이 시작될 수 있습니다. 따라서 V4를 시작하기 위해선 적어도 "10"의 시간이 걸립니다.
따라서 earlist[4] = early[6] = early[7] = 10이게 됩니다.
반대 개념이 존재하게 됩니다.
late[k]는 간선 k가 실행될 수 있는 가장 늦은 시간을 나타냅니다.
latest[j]는 정점 j가 일어날 수 있는 가장 늦은 시간을 나타내게 됩니다.
이번에도 위 그래프에서 V4를 봅시다. V7이 실행될 수 있는 가장 빠른 시간 ( = earlist[7] )은 "21"입니다. 맨 마지막이므로 V7이 실행될 수 있는 가장 늦은 시간 (=latest[7])도 "21"입니다. V4 -> V5 -> V7과정에서 "11"시간이 걸렸고, V4 -> V6 -> V7과정에서 "9"시간이 걸렸으므로 후자의 과정의 경우 전자 보다 "2"시간 늦게 작업을 시작해도 똑같이 끝낼 수 있습니다. 따라서 V4가 시작할 수 있는 가장 늦은 시간은 21 - 9 = "12"입니다.
Criticality라는 것도 있습니다. late[k] - early[k]를 나타내는 것인데, Criticality가 클수록 여유로운 놈이 됩니다. Criticality = 0인 작업을 Critical activity라고 하고, AOE네트워크의 목표는 작업들을 수행하는 데 걸리는 시간을 계산하는 것도 있지만, 그걸 통해 효율적으로 작업을 분배하기 위한 목적도 있습니다.
또한 critical path는 가장 긴 network path입니다.
예시
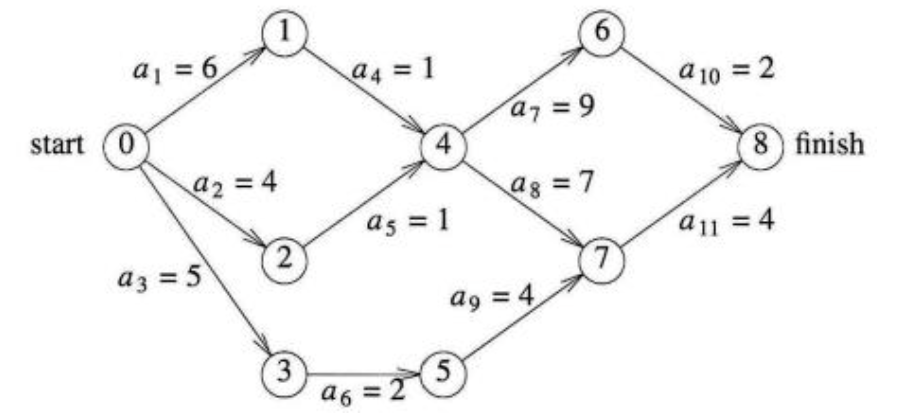
다음과 같은 AOE네트워크가 있다고 해 봅시다. 그럼 E0은 start of project가 되고, E4는 a1의 completion이 됩니다. ...
- critical path
- 0, 1, 4, 6, 8이 critical path가 되게 됩니다 (length = 18)
- earlist time
- E4가 일어날 수 있는 earlist time은 6 + 1인 7이 됩니다.
- earlist start time
- e(7) = e(8) = 7이 됩니다. earlist time이 7이기 때문입니다.
- latest time
- l(6) = 18 - 10 = 8, l(8) = 18 - 11 = 7
- critical activites
- e(8) = l(8) = 7
a5 -> e(5) = ee[2] = 4, l(5) = le(4) - duration of activity a5 = 7 - 1 = 6
a8 -> e(8) = ee(4) = 7, l(8) = le(7) - duration of activity a8 = 14 - 7 = 7
a8 is ctitical activity
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Sorting ( Quick Sort ) (0) | 2022.05.28 |
|---|---|
| Data Structure - Sorting ( Insertion Sort ) (0) | 2022.05.28 |
| Data Structure - Graph ( Floyd-Warshall Algorithm && Transitive Closure ) (0) | 2022.05.27 |
| Data Structure - Graph ( Dijkstra && Bellman and Ford Algorithm ) (0) | 2022.05.27 |
| Data Structure - Graph ( MST ) (0) | 2022.05.27 |
