Minimum Spanning Trees
- MST에서의 cost는 weighted undirected graph에서 sum of costs ( weights )를 말합니다.
- 또한 MST는 cost가 최소인 spanning tree를 말하게 됩니다.
- MST를 찾기 위해서는 3개의 알고리즘이 있습니다.
- Kruskal's, Prim's Sollin's algorithm이 있는데, 모드 greedy method에 기반되어 있습니다.
MST에서의 제약조건을 말씀드리겠습니다. 여기에서는
- 우리는 무조건 edge를 사용해야 합니다.
- 또한 우리는 정확히 n-1 edge를 MST를 그리는데 사용해야 합니다.
- 우리는 cycle을 가지는 edge를 만들어 내면 안됩니다.
Kruskal's Algorithm
신장 트리(Spanning Tree)는 기존 그래프의 모든 노드를 포함하지만 싸이클이 존재하지 않는 그래프 트리를 말합니다.


다음과 같은 그래프의 MST을 찾기 위해 Kruskal's Algorithm을 적용해 보도록 하겠습니다.
Kruskal's Algorithm은 먼저 가중치를 오름차순으로 정렬해서, 하나씩 그려나가면서, cycle이 생기지 않도록 그려주면 되는 아주 간단한 알고리즘입니다. 다만 코딩을 할 때 Cycle을 찾는 과정이 생각하기 어려워서 그렇지 매우 간단한 유명한 MST을 찾는 알고리즘입니다.
/kruskal.c
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_SIZE 100 #define INFINITE 100000 int Check[MAX_SIZE][MAX_SIZE] = {0}; void smallWeight(int rowSize, int colSize, int **Weight, int *checker) { int small = INFINITE, row, col; for (int i = 0; i < rowSize; i++) { for (int j = i + 1; j < colSize; j++) { if ((Check[i][j] > 0) && (small > Check[i][j])) { small = Check[i][j]; row = i, col = j; } } } // 최종적으로 -1로 초기화 해 줘야 한다. // 다시 체크 해 주지 않기 위해서 Check[row][col] = -1; Weight[0][*checker] = row; Weight[1][(*checker)++] = col; } int main(void) { FILE *fp_read = fopen("input.txt", "r"); if (fp_read == NULL) { fprintf(stderr, "File Open Error!"); exit(EXIT_FAILURE); } int count, EdgeCount = 0; fscanf(fp_read, "%d", &count); int Graph[MAX_SIZE][MAX_SIZE] = {0}; int temp; // 모든 간선들을 체크 하고 갯수를 저장해 줘야 한다. for (int i = 0; i < count; i++) { for (int j = 0; j < count; j++) { fscanf(fp_read, "%d", &temp); if (temp != 0 && (j > i)) { EdgeCount++; Graph[i][j] = temp; } } } for (int i = 0; i < count; i++) { for (int j = 0; j < count; j++) { Check[i][j] = Graph[i][j]; } } // 모든 간선의 개수만큼 반복을 하는데 // 이에 포함되어 있는 가중치를 작은 순서대로 저장해 줄 Weight 2차원 배열을 만들어 준다. int **Weight = malloc(sizeof(int *) * 2); for (int i = 0; i < 2; i++) { Weight[i] = malloc(sizeof(int) * EdgeCount); } int iterCount = 0; for (int i = 0; i < EdgeCount; i++) { smallWeight(count, count, Weight, &iterCount); // printf("%d %d\n", Weight[0][i], Weight[1][i]); } int *s = malloc(sizeof(int) * count); for (int i = 0; i < count; i++) { s[i] = i; } // 일단 선택된 간선을 기억하기 위한 2차원 배열을 만들어 주어야 한다. int **ReM = malloc(sizeof(int) * count); for (int i = 0; i < 2; i++) { ReM[i] = malloc(sizeof(int) * count); } // cost비용의 total value int totalCost = 0; int edgeCount = 0; int v1, v2; int s1, s2; int i = 0; while (edgeCount < (count - 1)) { // 간선에 연결된 두 정점을 저장하고 v1 = Weight[0][i], v2 = Weight[1][i]; s1 = s[v1], s2 = s[v2]; // 서로 두개가 다르면 ( subtree ) if (s1 != s2) { for (int j = 0; j < count; j++) { if (s[j] == s2) { s[j] = s1; } } ReM[0][edgeCount] = v1; ReM[1][edgeCount++] = v2; totalCost += Graph[v1][v2]; } i++; } printf("Selected Edges: "); for (int k = 0; k < count - 1; k++) { if (k == count - 2) printf("(%d, %d)", ReM[0][k], ReM[1][k]); else printf("(%d, %d),", ReM[0][k], ReM[1][k]); } printf("\nCost: %d\n", totalCost); fclose(fp_read); return 0; }
/input.txt
7 0 28 0 0 0 10 0 28 0 16 0 0 0 14 0 16 0 12 0 0 0 0 0 12 0 22 0 18 0 0 0 22 0 25 24 10 0 0 0 25 0 0 0 14 0 18 24 0 0
당연히 C++로 짜면 매우 간단해 질 코드입니다. 간단히 C언어 에서 가중치를 저장하는 Weight라는 2차원 배열을 만들고 이를 가중치의 오름차순으로 정렬을 시켰습니다. 그리고 s배열을 만든다음에 초기 상태로 초기화 하고, 가중치를 차례로 넣어가면서 s배열의 값을 edge중 작은 값으로 설정하며, cycle이 생기면 추가하지 않는 코드를 짜서 코드를 완성 시켰습니다.
Prim's Algorithm
Prim's Algorithm은 Kruskal's Algorithm보다 간단한데, 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 기법입니다. Prim's Algorithm은 매 순간 최선의 조건을 선택하는 그리디 알고리즘을 바탕에 둡니다. 죽 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택하면 됩니다.
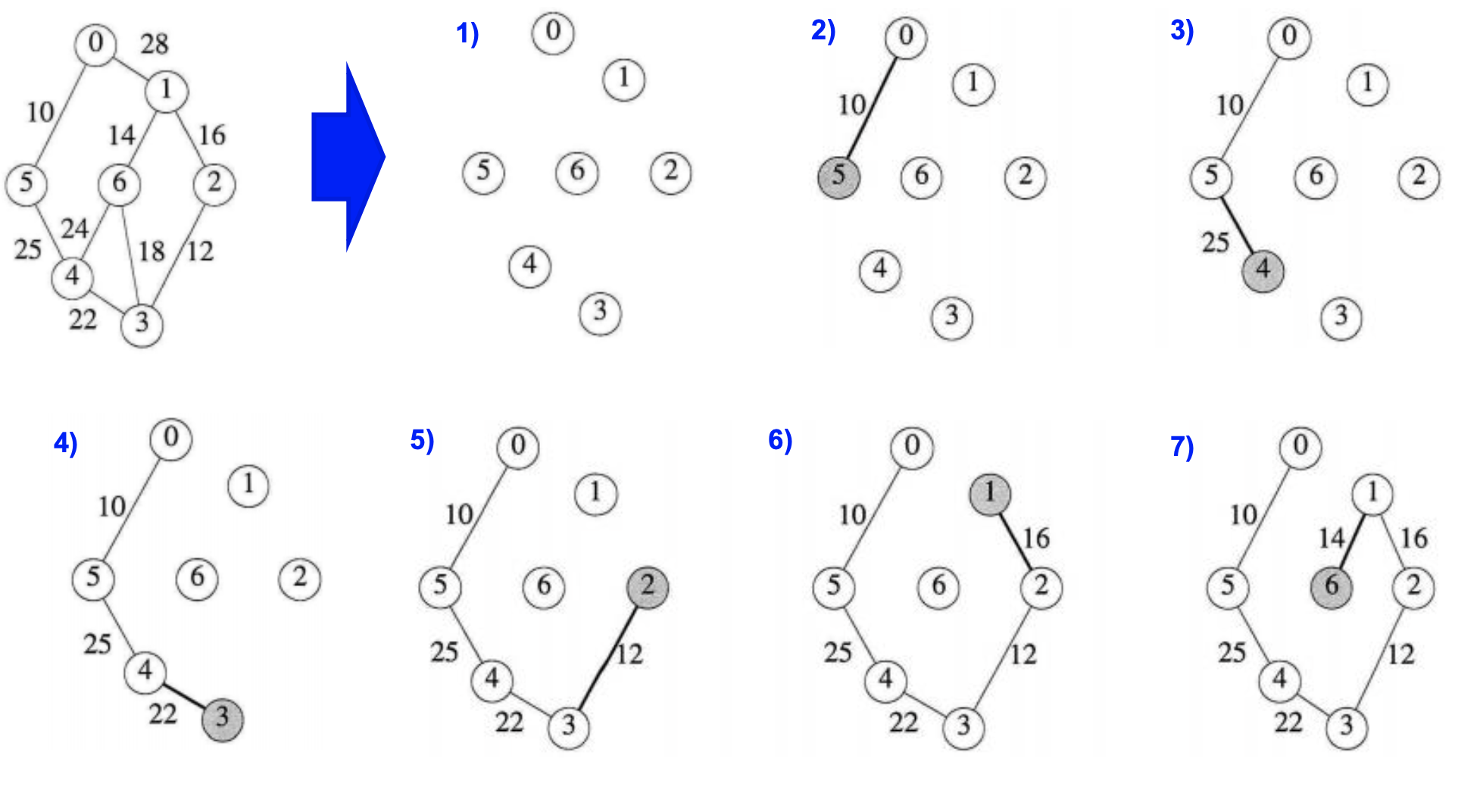
그림을 보면 간단히 이해할 수 있으리라 믿고 그냥 넘어가도록 하겠습니다.
Sollin's Algorithm
Sollin's Algorithm은 뭔가 직관적입니다.
- 각 Vertex마다 Weight가 낮은 것 하나씩 골라서 연결 ( 중복된 것이 있으면 무시 )
- tree가 하나 남을 때 까지 각 트리마다 위의 과정을 반복해 줍니다.
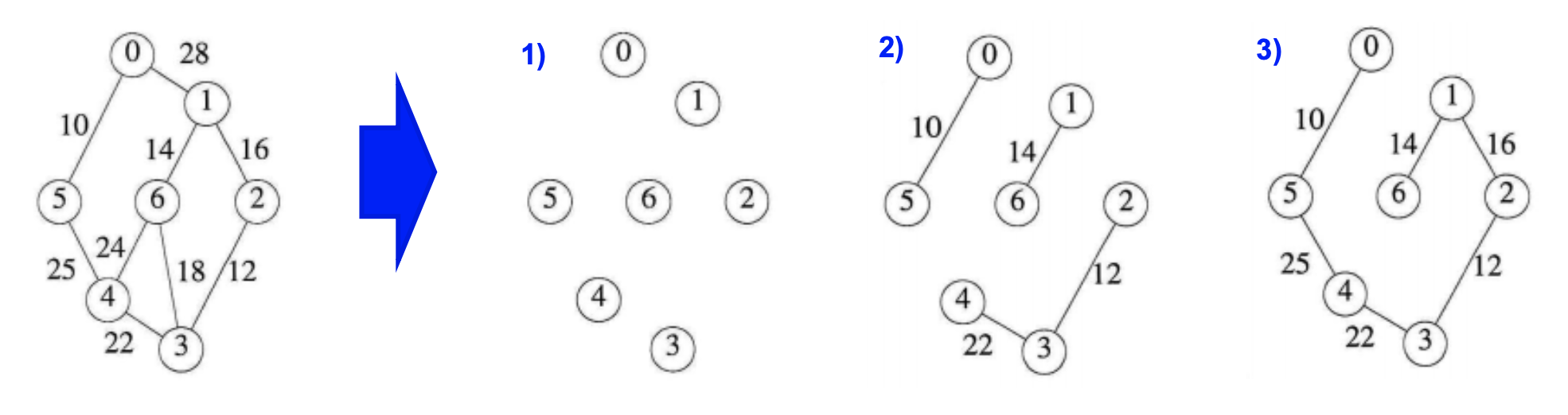
다음과 같이 첫번쨰 loop에서는 3개의 tree가 완성이 되었는데, 첫번째 loop에서 무시된 vertex는 3, 5, 6이여서 그렇다. 그리고 두번째 loop에서 {0, 5}Tree가 (5, 4)를 선택하고 나머지 2개 트리가 (1, 2)를 선택함 으로써 트리를 완성시키면 됩니다.
이는 매번 최대 n개, n/2개, n/4개 ... 의 Vertex를 검사하게 되고 (O(logn)), edge를 다 검사하게 되므로 (O(n)) -> Solin알고리즘의 시간 복잡도는 O( n log n )이 됩니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Graph ( Floyd-Warshall Algorithm && Transitive Closure ) (0) | 2022.05.27 |
|---|---|
| Data Structure - Graph ( Dijkstra && Bellman and Ford Algorithm ) (0) | 2022.05.27 |
| Data Structure - Graph ( Biconnected Components ) (0) | 2022.05.27 |
| Data-Structure - Arrays and Structure (0) | 2022.04.16 |
| Data-Structure - Tree (0) | 2022.04.14 |
