Biconnected Components
- articulation point란 G의 vertex v를 deletion했을 떄, 최소한 2개의 컴포넌트로 쪼개지면 이때의 vertex를 articulation point라고 한다.

이 떄 biconnected graph란 연결그래프인데 articulation point가 없는 그래프를 말합니다. 많은 그래프에서 articulation points는 탐탁치 않습니다.

- biconnected component는 maximal biconnected subgraph of G입니다.
- 즉 2개의 biconnected component에서 한개 보다 많은 공통된 vertex를 가질 수는 없습니다.
- 또한 biconnected component에서 하나의 edge는 2개가 들어갈 수 없습니다.

이러한 biconnected component를 찾기 위한 알고리즘이 있습니다. 먼저 depth first spanning tree가 G의 biconnected component를 찾는데 도움을 줍니다.

여기서 nontree edge (u, v)는 back edge라고 하는데, 이는 dfs과정을 거치면서 포함되지 않은 edge라고 보면 됩니다.
Finding Articulation Point
여기서 저희는 low라는 value를 선언해 주어야 합니다. low의 정의 방식은 이러합니다. 각각의 vertex에 대해서 low(u)는 the lowest depth first number입니다. 그런데 저희는 0개 혹은 더 많은 u의 후손이나 back edge를 통해서 갈 수 있는 depth first number까지 포함합니다.
즉 위의 그래프에서 vertex마다의 dfn과 low value를 매칭시켜서 표를 그려보게 되면

다음과 같이 그려지게 된다.
이제 우리는 다음과 같이 articulation point를 찾을 수 있게 된다.
sapanning tree의 root가 2개 이상의 children을 가지고 있거나, u가 루트가 아니라면 child w를 가지고 있는데 low(w) >= dfn(u)를 만족 한다면 u는 articulation point가 된다.
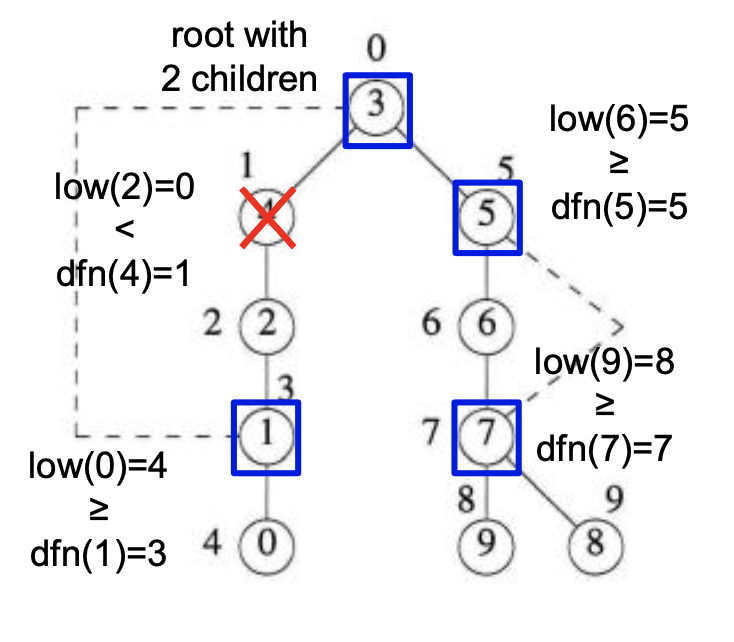
다음과 같이 1, 3, 5, 7이 articulation point임을 알 수 있는데, 예를 들어서 몇개를 해보면, Vertex1 child w의 dfn(1) = 3입니다. 하지만 child의 low value low(0) = 4인데 low(w) >= dfn(u)를 만족하므로 1은 articulation point가 됩니다. 다음으로 1을 예시를 들어보면 child는 vertex 2를 가지고 있는데, dfn(4) =1을 가지고 있고 low(2) = 0인데 dfn(4) > low(0)이므로 articulation point가 될 수 없다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Graph ( Dijkstra && Bellman and Ford Algorithm ) (0) | 2022.05.27 |
|---|---|
| Data Structure - Graph ( MST ) (0) | 2022.05.27 |
| Data-Structure - Arrays and Structure (0) | 2022.04.16 |
| Data-Structure - Tree (0) | 2022.04.14 |
| Data-Structure - Linked-List ( Application - 3 ) (0) | 2022.04.08 |
