Shortest Paths
- Path finding system은 그래프를 이용하는 시스템을 말합니다.
Single Source / All Destinations : Nonnegative Edge Costs
- directed graph G=(V, E)에서 weighting function w(e)에서 source vertex v0을 바탕으로 a shortest path를 찾는 과정을 말합니다.
여기서 중요한 점은 w(e) > 0입니다. negative을 찾는 방법은 아래에서 다룹니다.

예를 들면 다음과 같습니다. v0에서 v1로 갈 수 있는 a shortest path는v0 -> v3 -> v4 -> v1이 됩니다. v0 -> v3이 아니라요. 이러한 a shortest path를 찾는 알고리즘을 소개합니다.
Dijkstra Algorithm

다익 스트라 알고리즘의 간단한 예시 입니다. 이를 직접 코드로 짜 보도록 하겠습니다.
/Dijkstra.c
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <limits.h> #define INFINITE (INT_MAX) / (2) #define FALSE 0 #define TRUE 1 int *distance; short int *found; int selecMinVertex(int *distance, int vertexNum, short int *found) { int min = INFINITE, minPos = -1; for (int i = 0; i < vertexNum; i++) { if ((distance[i] < min) && !found[i]) min = distance[i], minPos = i; } return minPos; } void shortestPath(int startEdge, int **cost, int *distance, int vertexNum, short int *found) { int nextVertex; // 시작 정점에 대한 데이터 초기화를 해주어야 한다. for (int i = 0; i < vertexNum; i++) { found[i] = FALSE; distance[i] = cost[startEdge][i]; } found[startEdge] = TRUE; // 처음 노드는 distance = 0으로 초기화 해주어야 한다. distance[startEdge] = 0; // 이제 found가 False이고 가중치가 가장 낮은 것을 찾는 과정을 처리해 주어야 한다. for (int j = 0; j < vertexNum - 2; j++) { nextVertex = selecMinVertex(distance, vertexNum, found); found[nextVertex] = TRUE; // 반복하면서 더 짧은 거리가 있나 찾아주는 과정이 있어야 한다. for (int i = 0; i < vertexNum; i++) { if (distance[nextVertex] + cost[nextVertex][i] < distance[i]) distance[i] = distance[nextVertex] + cost[nextVertex][i]; } } } int main(void) { FILE *fp_read = fopen("input.txt", "r"); if (fp_read == NULL) { fprintf(stderr, "File Open Error!"); exit(EXIT_FAILURE); } int vertexNum, startEdge; fscanf(fp_read, "%d", &vertexNum); fscanf(fp_read, "%d", &startEdge); int **cost = (int **)malloc(sizeof(int *) * vertexNum); for (int i = 0; i < vertexNum; i++) cost[i] = (int *)malloc(sizeof(int) * vertexNum); int temp; for (int i = 0; i < vertexNum; i++) { for (int j = 0; j < vertexNum; j++) { fscanf(fp_read, "%d", &temp); if (temp != 0) cost[i][j] = temp; else cost[i][j] = INFINITE; } } found = (short int *)malloc(sizeof(short int) * vertexNum); distance = (int *)malloc(sizeof(int) * vertexNum); shortestPath(startEdge, cost, distance, vertexNum, found); for (int i = 0; i < vertexNum; i++) printf("%d ", distance[i]); for (int i = 0; i < vertexNum; i++) free(cost[i]); free(found); free(distance); free(cost); fclose(fp_read); return 0; }
/input.txt
8 4 0 0 0 0 0 0 0 0 300 0 0 0 0 0 0 0 1000 800 0 0 0 0 0 0 0 0 1200 0 0 0 0 0 0 0 0 1500 0 250 0 0 0 0 0 1000 0 0 900 1400 0 0 0 0 0 0 0 1000 1700 0 0 0 0 0 0 0

이렇게 하게 되면 distance 배열안에 start vertex를 v4로 했을 때의 a shortest path를 구할 수 있게 됩니다.
코드를 잠깐 리뷰해 봅시다. 기본적으로 노드에 대해서 경로 수정을 했는지 checking하기 위한 found배열이 하나 필요합니다. 그리고 가중치 ( adjacent matrix )들을 저장하기 위한 cost 2차원 배열이 필요합니다. vertexNum * vertexNum크기의 cost 2차원 배열을 선언할 때 중요한 점은 갈 수 없는 경로는 INFINITE로 지정해 주어야 한 다는 점입니다.
그 다음으로 본격적으로 Dijkstra알고리즘이 시작되는데, 초기에 distance배열을 cost adjacent matirix의 값으로 초기화 하고 found에 시작 vertex를 넣어 줍니다. 그리고 selectMinVertex 함수를 사용해서 그 다음 최적화 하기 위한 ( !found[i] && distance[i] < min )즉 방문 하지는 않았는데, distance가 최소인 vertex를 찾아서, found에 다시 넣고 distnace배열의 값을 조정해 줍니다.
distance배열의 값은 distance[nextVertex] + cost[nextVertex][i] < distance 즉 기존의 distance의 값과 nextVertex을 경유해서 간 값을 비교해서 전자의 값이 더 크다면 더 작은 nextVertex를 경유해서 간 값으로 초기화 하는 겁니다. 이러한 과정을 vertexNum - 2번 반복하다 보면 위와 같이 distance배열이 a shortest path로 초기화 되게 됩니다.
Single Source / All Destinations : General Weights
우리는 이제 좀 더 general case를 생각해야 합니다. w(e) < 0도 포함되는 상황을 말이죠

다음과 같이 길이에 음수가 있는 경우 Dijkstra Algorithm을 계산해 보면 v0 -> v2의 최적의 cost값을 5라고 줍니다. 하지만 아니죠 최적은 7 + (-5)해서 2가 될겁니다.
또한 negative edge length가 허용된다면 우리는 cycle이 없는 그래프를 그려야 할 겁니다.

다음과 같이 최적의 경로가 -INFINITE가 되어 찾을 수 없게 되게 때문입니다.
Bellman and Ford Algorithm
즉 예시와 함꼐 정리해 보도록 하겠습니다.
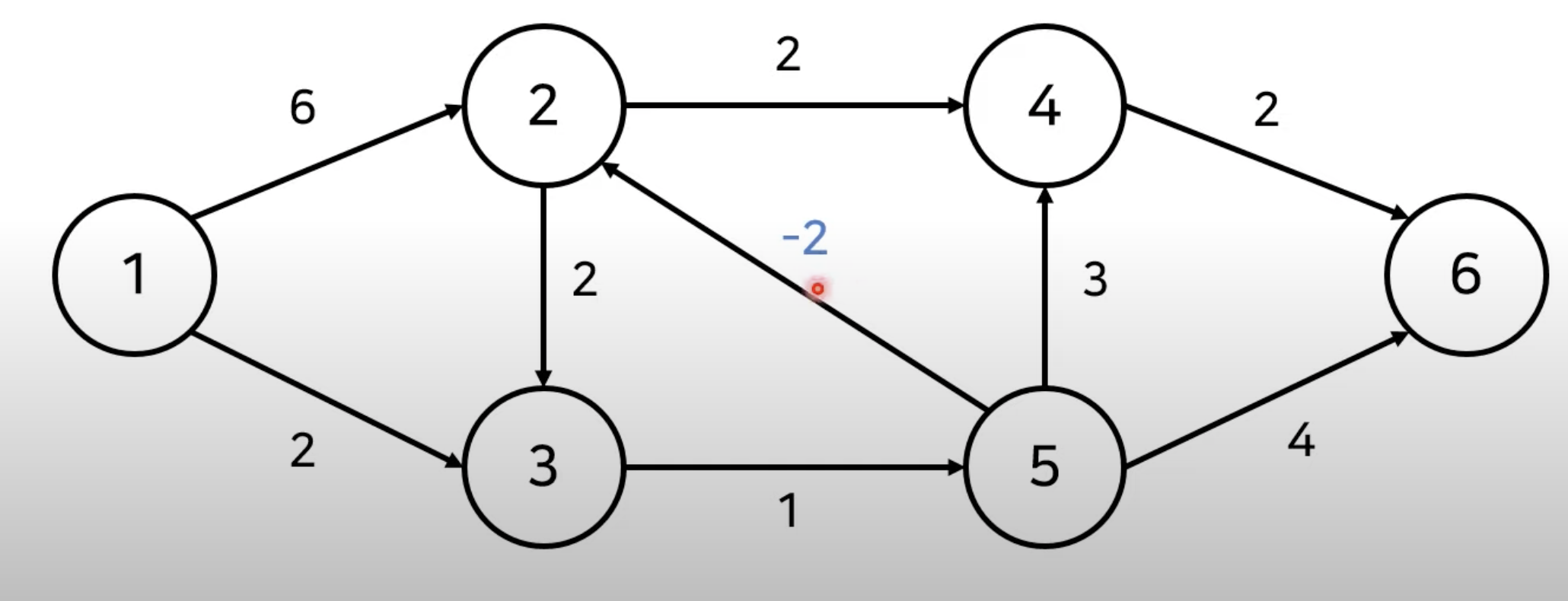
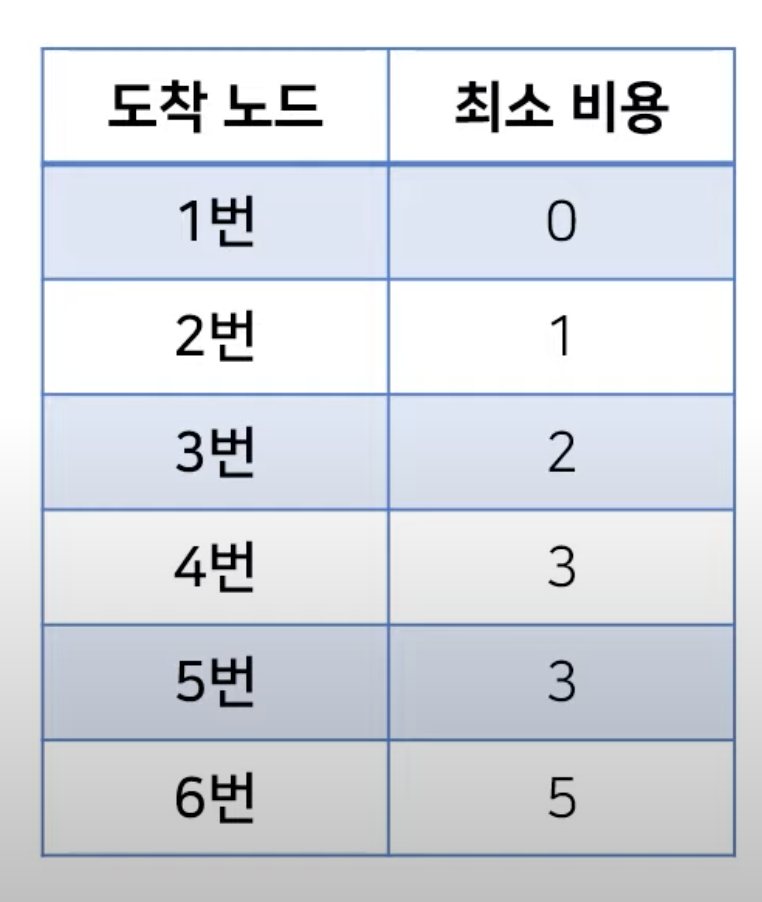
- 위의 그래프에서는 음수 간선이 포함되어 있습니다.
- 이는 Bellman Ford 알고리즘으로 계산할 수 있게 됩니다.
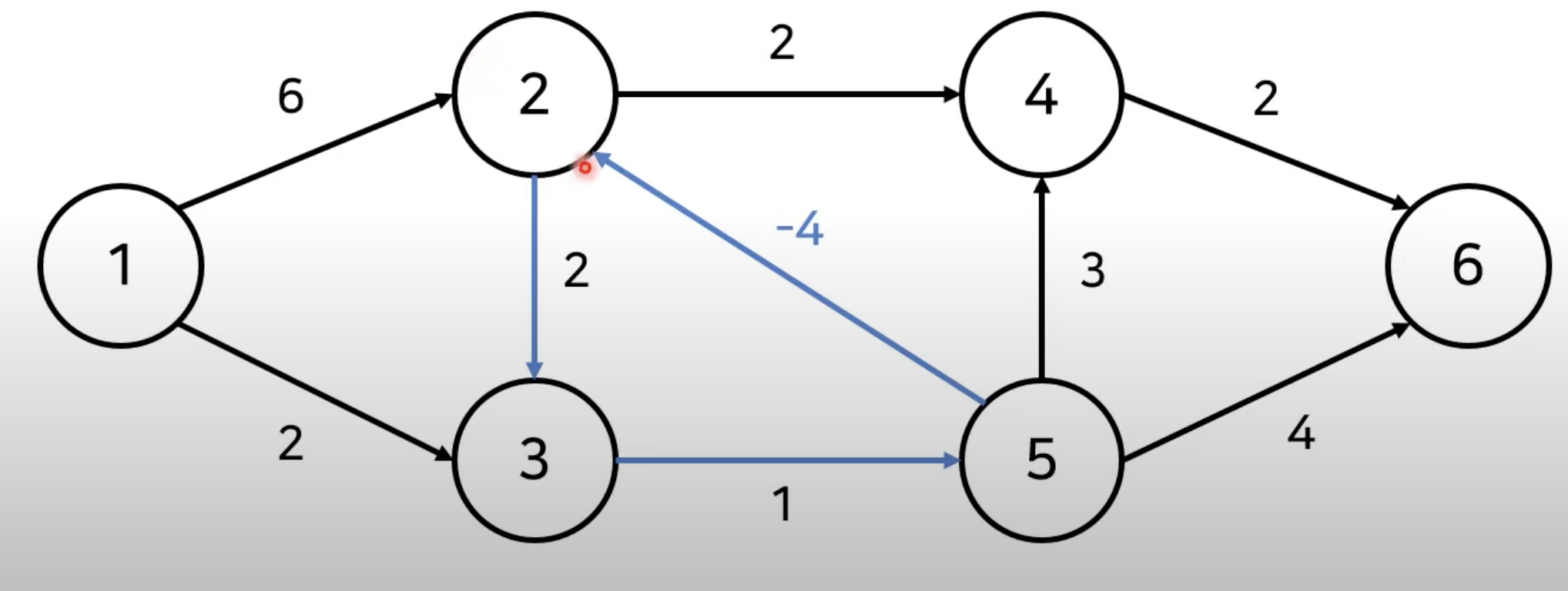
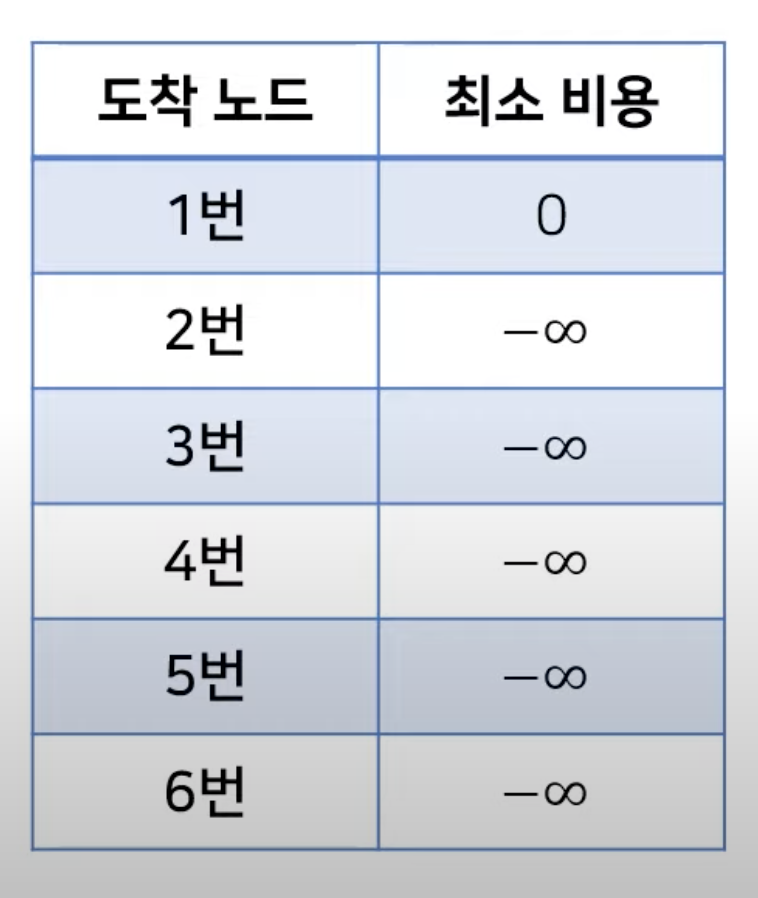
- 하지만 음수 간선의 순환이 이루어 진다면 어떻게 해야 할까요?
- 위의 그래프에서는 음수 간선의 순환이 포함되어 있습니다.
- 이 경우 최단 거리가 음의 무한인 노드가 발생하게 됩니다.
- 음수 간선에 관하여 최단 경로 문제는 다음과 같이 분류할 수 있게 됩니다.
- 모든 간선이 양수인 경우
- 음수 간선이 있는 경우
- 음수 간선 순환은 없는 경우
- 음수 간선 순환이 있는 경우
- 벨만 포드 최단 경로 알고리즘은 음의 간선이 포함된 상황에서도 사용할 수 있습니다.
- 또한 음수 간선의 순환을 감지할 수 있습니다.
- 벨만 포드의 기본 시간 복잡도는 O(VE)로 다익스트라 알고리즘에 비해 조금 느리게 됩니다.
Bellman and Ford Algorithm Process
- 출발 노드를 설정합니다.
- 최단 거리 테이블을 초기화 합니다.
- 다음의 과정을 N - 1번 반복합니다.
- 전체 간선 E개를 하나씩 확인합니다.
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신합니다.
만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번의 과정을 한 번 더 수행합니다.
- 다익스트라 알고리즘
- 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하게 됩니다.
- 음수 간선이 없다면 최적의 해를 찾을 수 있습니다.
- 벨만 포드 알고리즘
- 매번 모든 간선을 전부 확인합니다.
- 따라서 다익스트라 알고리즘에서의 Optimal한 Solution을 항상 포함하게 됩니다.
- 다익스트라 알고리즘에 비해서 시간이 오래 걸리지만 음수 간선 순환을 탐지할 수 있습니다.
- 매번 모든 간선을 전부 확인합니다.
concept
Bellman and ford algorithm은 s, u사이의 최단 경로를 구할 때 그래프 내 모든 엣지에 대해 edge relaxation을 수행해 줍니다. 생각해 보면 s, u사이의 최단 경로는 s와 u뿐일 수 있고, u를 제외한 그래프의 모든 노드 (|V| - 1개)가 s, u사이의 최단경로를 구성할 수도 있습니다. 따라서 Bellman and ford algorithm은 모든 엣지에 대한 edge-relaxation을 |V|-1회 수행합니다.
수행 예시 1

첫번쨰 relaxation과정을 해보겠습니다. (B, E)를 보겠습니다. 무한대-2=무한대 이므로 업데이트 할 필요가 없습니다. (C, E), (F, C), (D, F), (C, B)또한 마찬가지 입니다. (A, B)의 경우 시작노드 A에서 B에 이르는 거리가 8이고, 이는 기존 거리(무한대)보다 작으므로 8을 B에 기록해 둡니다. 마찬가지로 C, D도 각각 -2, 4로 기록해 둡니다. 이로서 그래프 모든 엣지에 대한 첫번쨰 edge relaxation이 끝났습니다,
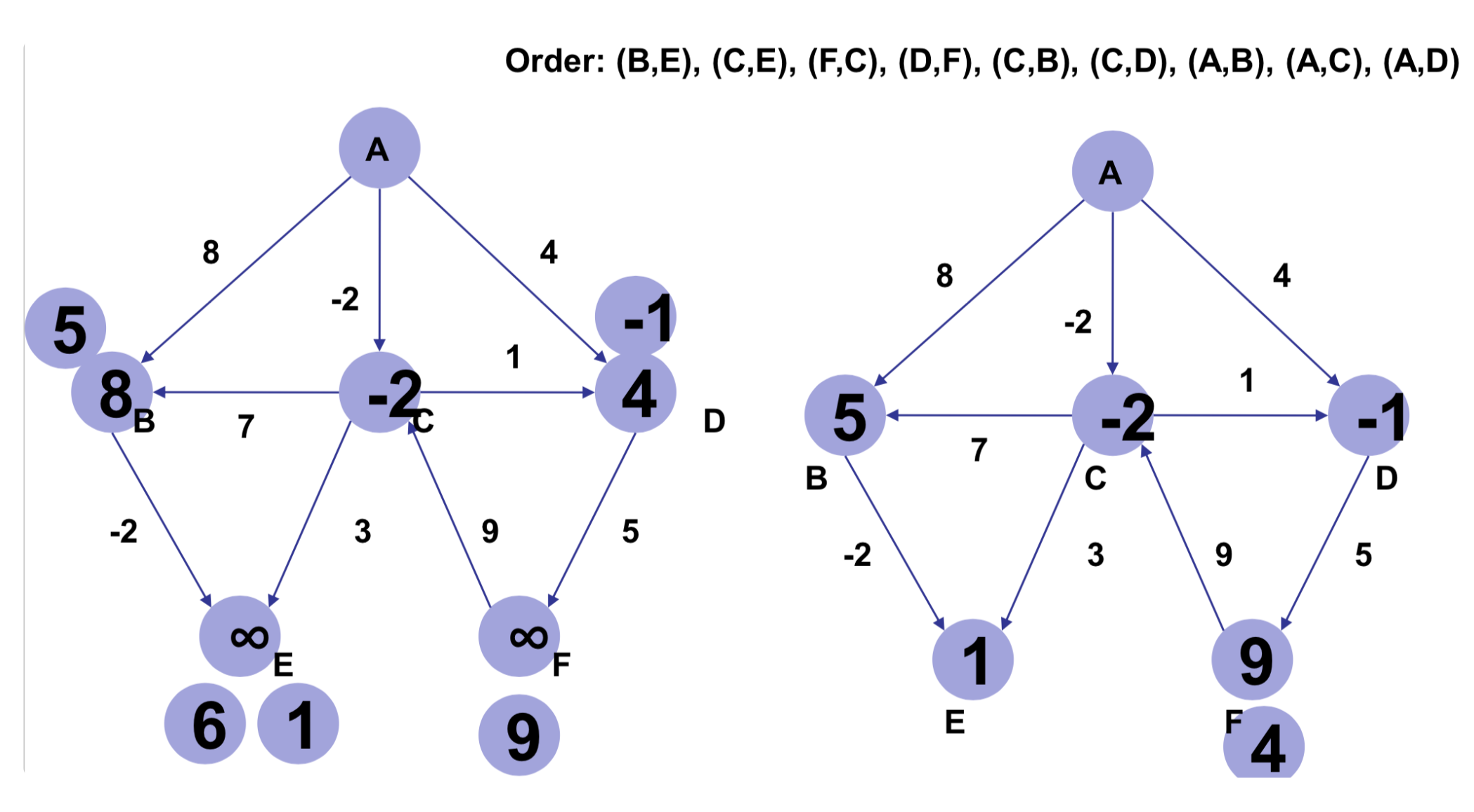
상단 좌측 차례입니다. (B, E)의 경우 8-2=6이고 이는 기존 거리 (무한대)보다 작으모로 6을 E에 기록해 둡니다. (C, E)의 경우 -2+3=1이고 기존 거리 (6)보다 작으므로 1을 E에 기록해 둡니다. 이를 모든 edge(간선)에 대해 수행해 주면 좌측 상단 그림과 같은 상태가 되고
이를 한번 더 수행해 주면 상단 우측과 같은 상태가 되며 총 |V| - 1 5번 반복해 주면 Bellman and Ford Algorithm의 최종 결과물이 나오게 됩니다.
negative cycle
하지만 Bellman and Ford Algorithm은 앞에서 말한 것과 같이 음수 가중치가 사이클을 이루고 있는 경우에는 작동하지 않습니다.
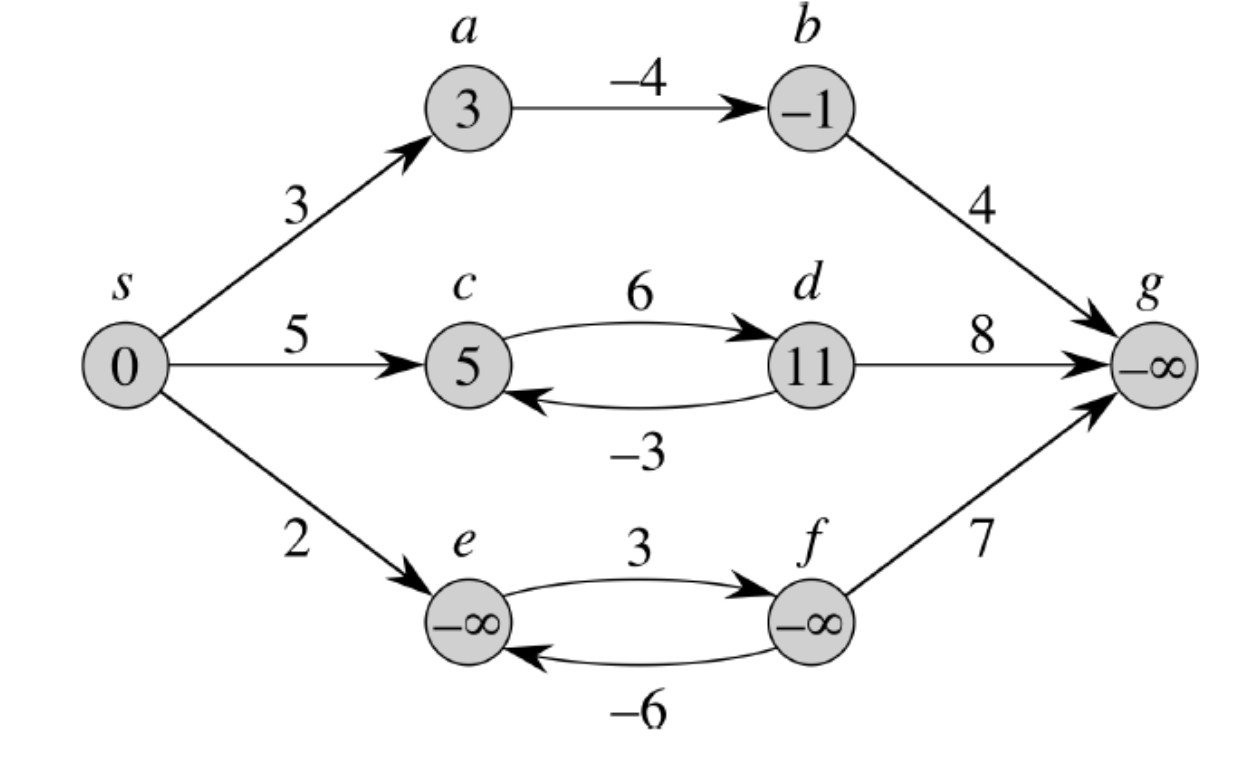
위 그림에서 c, d그리고 e, f가 사이클을 이루고 있는 걸 확인할 수 있습니다. c, d의 경우 사이클을 돌 수록 거리가 커져서 최단경로를 구할 때 문제가 되지 않습니다. 반면 e, f의 경우 사이클을 돌면 돌수록 그 거리가 작아져 Bellman and Ford Algorithm으로 최단 경로를 구하는 것 자체가 의미가 없어집니다.
따라서 그래프 모든 엣지에 대해 edge relaxation을 시작노드를 제외한 전체 노드수 만큼 반복 수행한 뒤, 마지막으로 그래프 모든 엣지에 대해 edge relaxation을 1번 수행해 줍니다. 이 때 한번이라도 업데이터가 일어난다면 위와 같은 negative cycle이 존재한다는 뜻이 되어서 결과를 수할 수 없다는 의미의 false를 반환하고 함수를 종료하게 됩니다.

Bellman and Ford Algorithm의 전체 의사 코드는 다음과 같습니다.
계산 복잡성
벨만 포드 알고리즘은 그래프 모든 엣지에 대해 edge relaxation을 시작 노드를 제외한 전체 노드수 만큼 반복 수행하고, 마지막으로 그래프 모든 엣지에 대해 edge relaxation을 1번 수행해 주므로, 그 계산 복잡성은 O(|V||E|)이 됩니다. 그런데 dense graph의 엣지 수가 대개 노드 수의 제곱에 근사하므로 간단하게 표현하면 O(|V|^3)이 됩니다. 이는 다익스트라 알고리즘 (O|V|^2)보다 더 큰데, 벨만-포드 알고리즘은 음수인 가중치까지 분석할 수 있기 때문에 일종의 trade-offf라고 생각해도 될 것 같습니다.
'School > DataStructure' 카테고리의 다른 글
| Data Structure - Graph ( AOV, AOE Network ) (0) | 2022.05.27 |
|---|---|
| Data Structure - Graph ( Floyd-Warshall Algorithm && Transitive Closure ) (0) | 2022.05.27 |
| Data Structure - Graph ( MST ) (0) | 2022.05.27 |
| Data Structure - Graph ( Biconnected Components ) (0) | 2022.05.27 |
| Data-Structure - Arrays and Structure (0) | 2022.04.16 |
