Equivalent Relations

Equivalent Relation이란 symeetric, relfexive, transitive을 모두 다 만족하는 관계를 말합니다.

간단한 예시는 위와 같습니다. 이는 매우 중요한데, 그 이유는 equivalent relation이 signal net을 검증하기 때문입니다. equivalence를 결정하는 알고리즘은 아래와 같습니다.

2D array representation
위의 알고리즘을 구현하기 위해서는, 2차원 배열 pairs[n][m]이 사용되어야 합니다. 여기서 m은 related pairs의 개수고, n은 objects의 개수입니다. 하지만 이는 엄청난 공간 낭비를 할 수 있습니다. 그 이뉴능 아주 적은 배열의 값만이 사용될 수도 있기 때문입니다. 또한 <i, j> pair를 넣을 경우, i번째 행의 다음 공간을 찾을려면 많은 시간이 필요하기 때문입니다.

Linked List representation
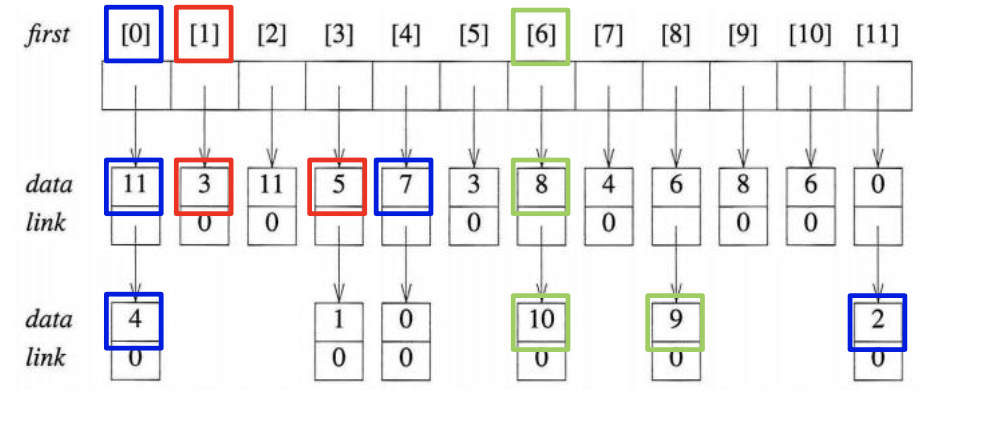
또한 Linked List로 2D array로 구현하던걸 구현하면 불필요한 메모리의 낭비를 해결할 수 있습니다. 이를 해결하기 위해서는 두가지 배열을 사용해야 합니다. seq[n]과 out[n]입니다. 이의 역할을 아래와 같습니다.



결과적으로 우리는 위의 그림처럼 코드를 구상하여야 합니다.
equivalent-linked-list.c
#include <stdio.h> #include <stdlib.h> #define MALLOC(p, s) \ if (!((p) = malloc(s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } #define REALLOC(p, s) \ if (!((p) = realloc(p, s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } #define FALSE 0 #define TRUE 1 typedef struct node_ { int data; struct node_ *link; } node, *nodePointer; int main(void) { FILE *fp_read; if ((fp_read = fopen("input.txt", "r")) == NULL) { fprintf(stderr, "File Open Error!"); return 0; } int objectNumber, pairNumber, k; fscanf(fp_read, "%d", &objectNumber); fscanf(fp_read, "%d", &pairNumber); short *out; MALLOC(out, sizeof(short) * objectNumber); nodePointer *seq; MALLOC(seq, sizeof(nodePointer) * objectNumber); for (k = 0; k < objectNumber; k++) { out[k] = TRUE; } // 추가할 pair의 node nodePointer x; int i, j; for (k = 0; k < pairNumber; k++) { MALLOC(x, sizeof(node)); fscanf(fp_read, "%d %d", &i, &j); x->data = j; x->link = seq[i]; seq[i] = x; MALLOC(x, sizeof(node)); x->data = i; x->link = seq[j]; seq[j] = x; } nodePointer temp, temp2, top = NULL; for (i = 0; i < objectNumber; i++) { if (out[i] == TRUE) { if (i == 0) { printf("new class: %5d", i); } else { printf("\nnew class: %5d", i); } out[i] = FALSE; temp = seq[i]; while (TRUE) { while (temp) { j = temp->data; if (out[j]) { printf("%5d", j); out[j] = FALSE; temp2 = temp->link; temp->link = top; top = temp; temp = temp2; } else { temp = temp->link; } } if (!top) break; temp = seq[top->data]; top = top->link; } } } free(x); fclose(fp_read); return 0; }
input.txt
12 9 0 4 3 1 6 10 8 9 7 4 6 8 3 5 2 11 11 0
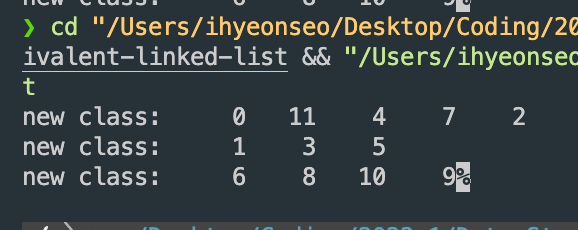
위의 그림에 있던 예제대로 코드를 짜고 동일한 equivalent-class끼리 출력을 했습니다.
알고리즘의 기본적인 형태는 위와 같고, 코드의 핵심은 top을 만들어서 노드를 하나씩 출력한 다음에 재귀적으로 계속 부르고 출력 한 것은 출력하지 않는 것입니다.
Equivalence Classes 총 정리
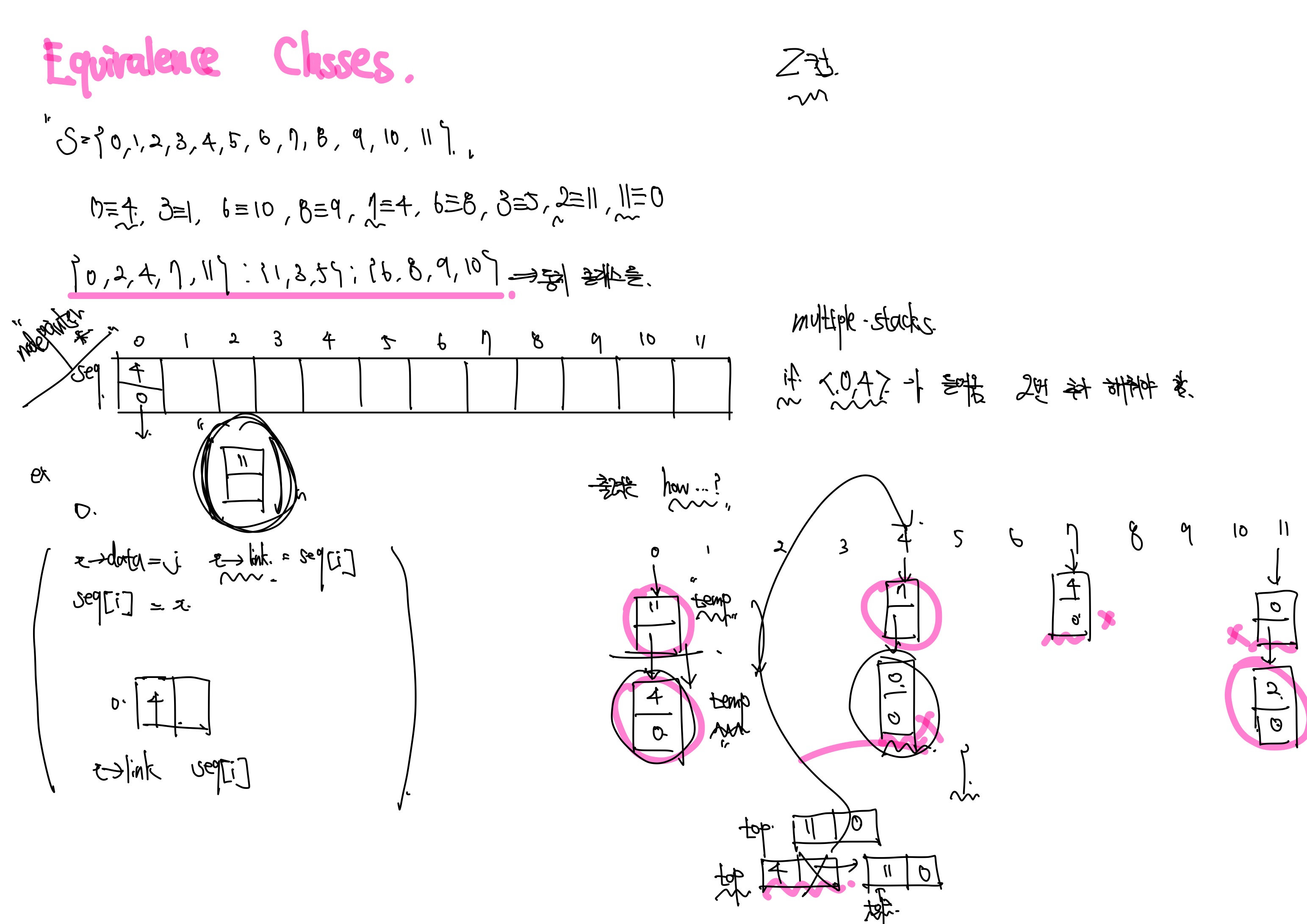
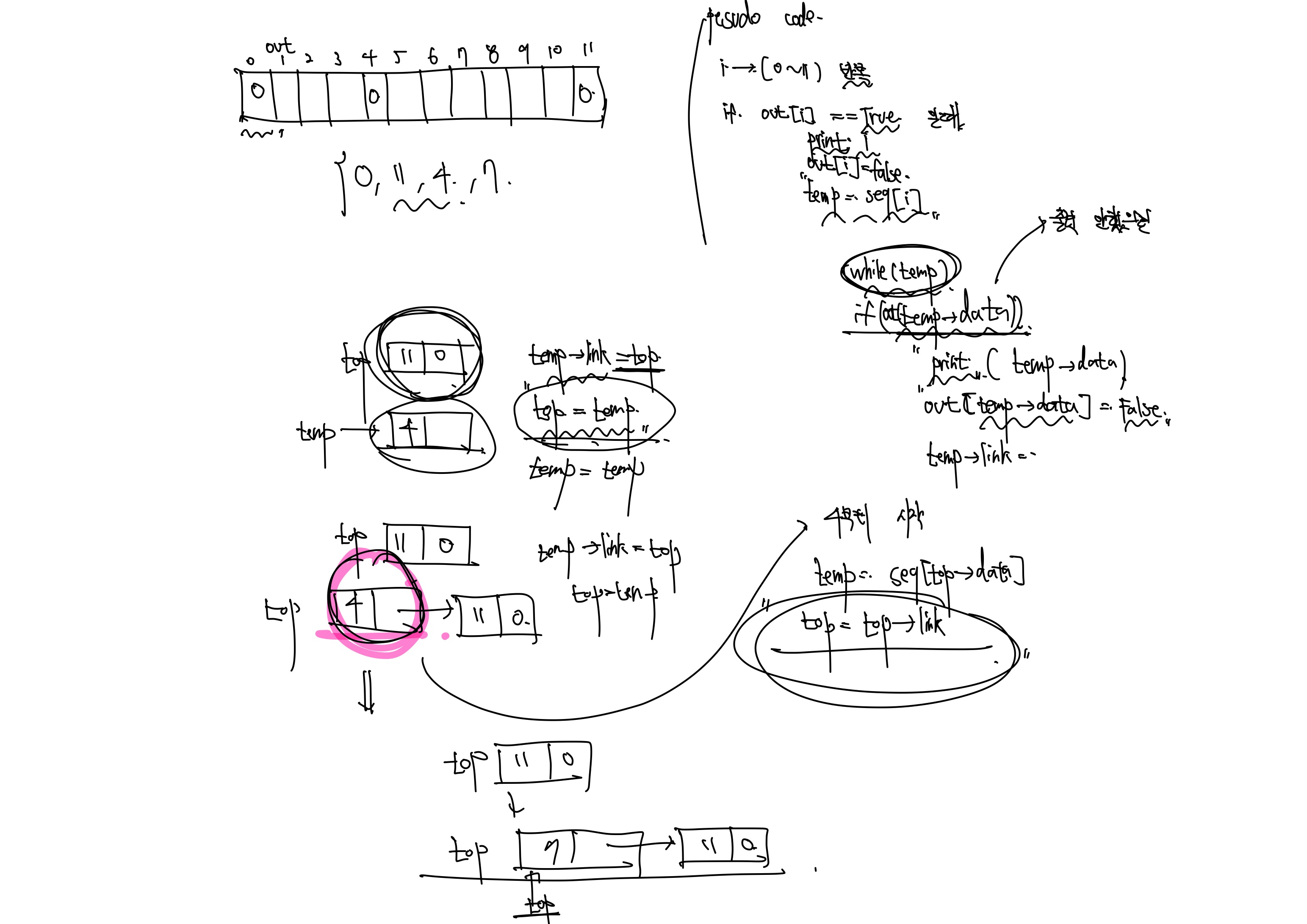
Sparse Matrices

linked-list로 sparse matrices를 나타내기 위해서는 Header Nodes와 Entry Nodes가 필요하다. 이를 구현하기 위해서는 2가지의 구조체와 공통된 부분을 위한 공용체가 필요하다.
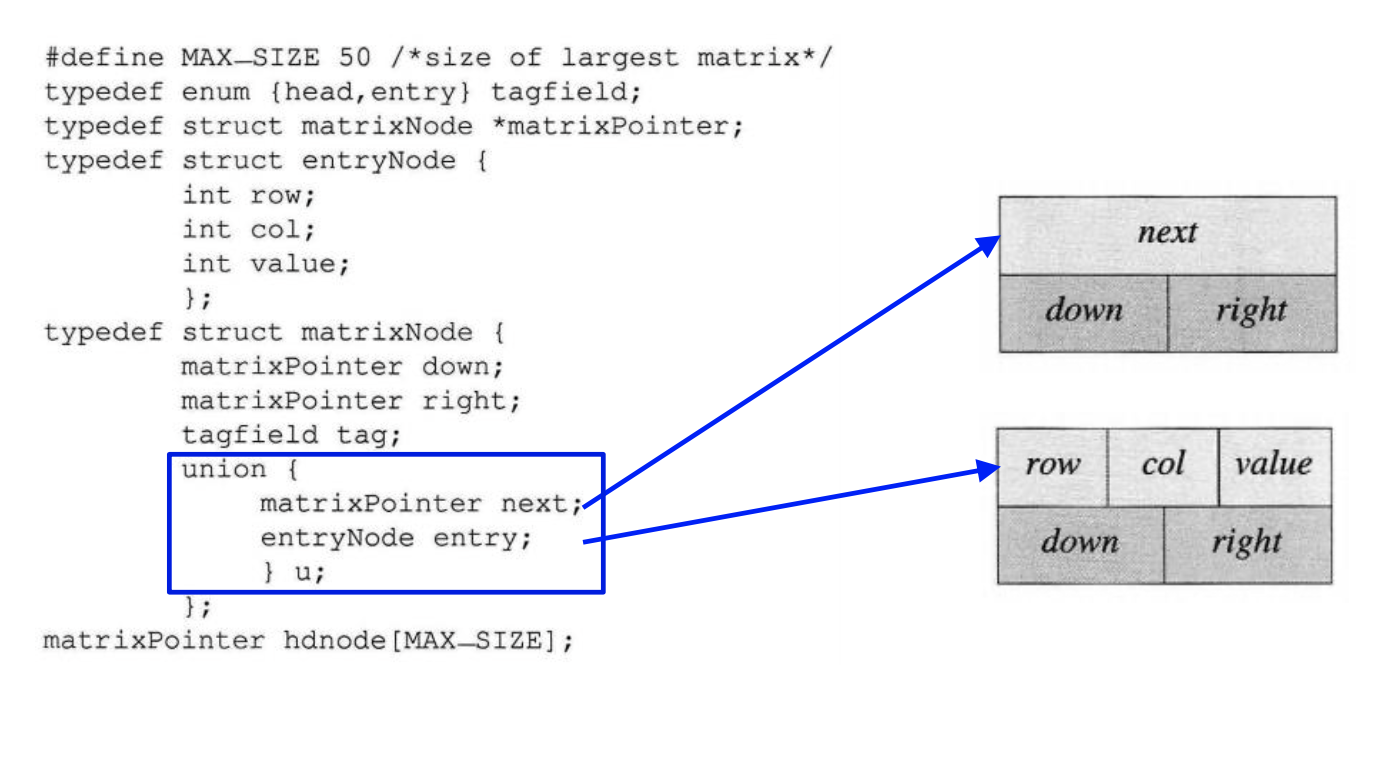
이와같이 간단하게 구현할 수 있고 다음은 얘시 5*4 sparse matrix를 위 구조체와 공용체를 어떻게 구현할 수 있는지 보겠습니다.
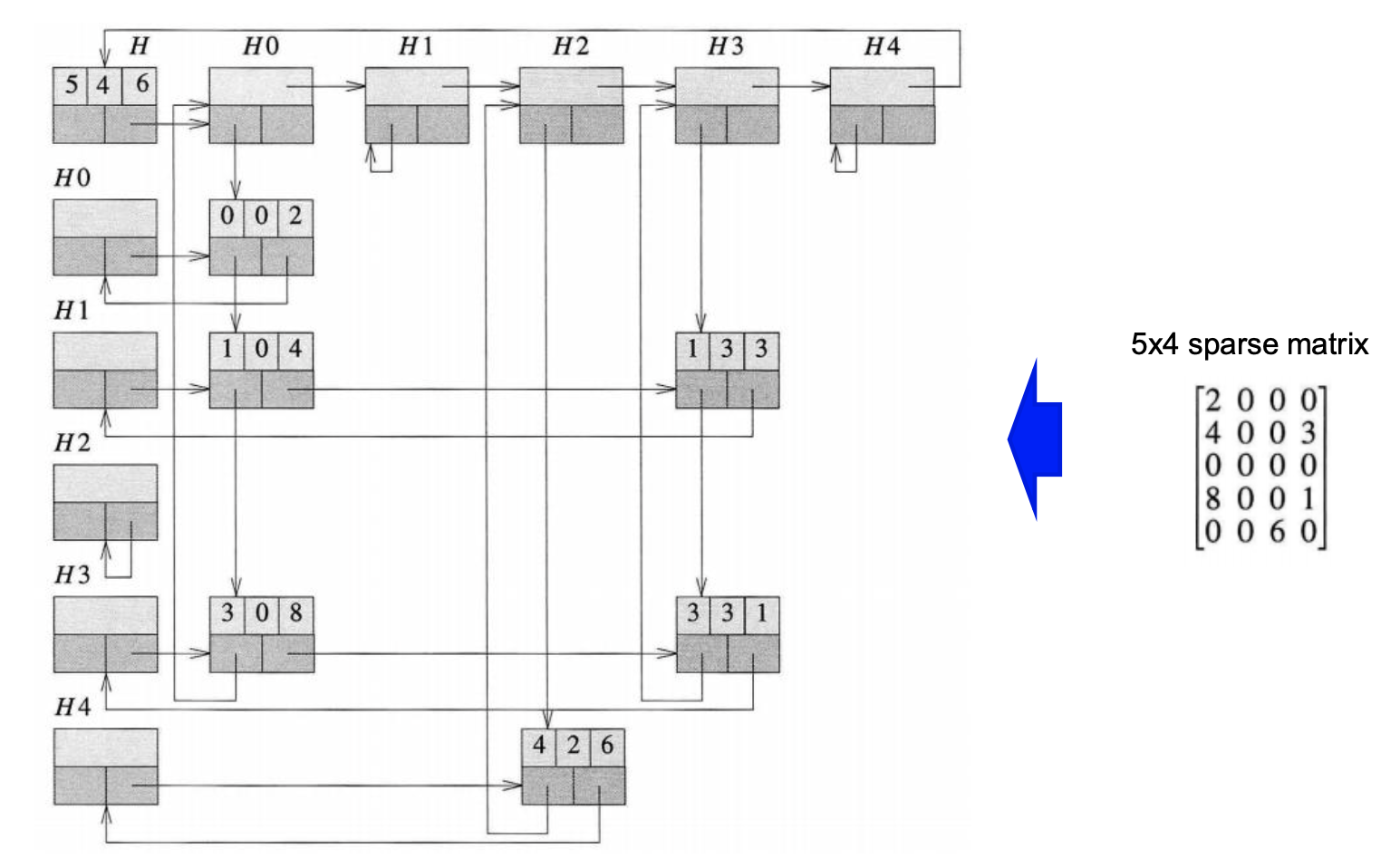
보기 편하기 위해서 H0~H4를 2번 쓴것이고 그냥 2차원 배열을 쓰는 것처럼 down과 right의 matrixPoitner타입의 변수를 잘 활용해 주면 충분히 공간의 낭비없이 구현 가능합니다.
Doubly Linked Lists
Doubly Linked Lists는 기존의 linked-list와 다르게 양방향으로 움직일 수 있습니다. 이는 임의의 노드를 제거할 때 매우 유용하게 사용될 수 있는 자료형태 입니다. 각각의 노드는 최소한 3개의 필드를 가집니다. 형태는 아래와 같습니다.
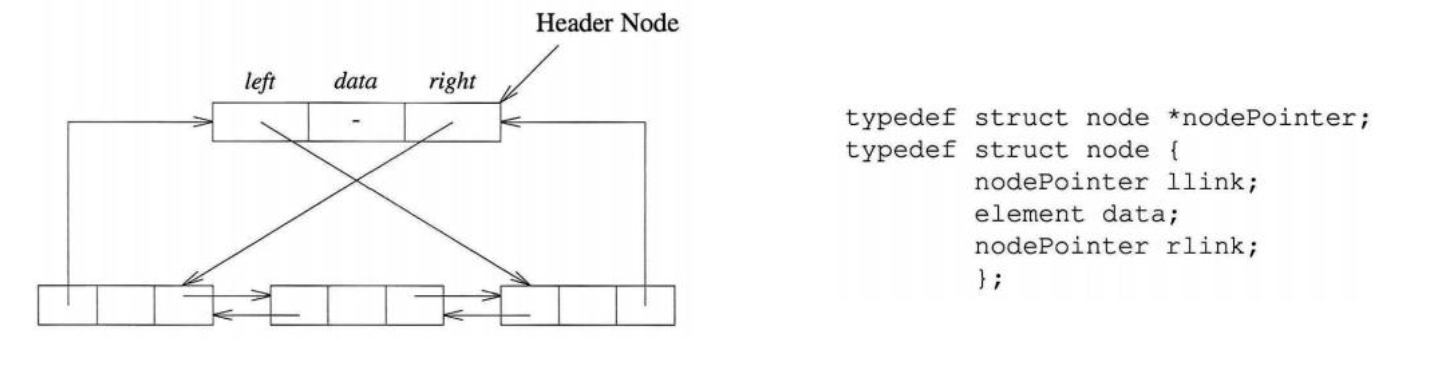
이제 doubly-linked-list의 기본 연산함수에 대해서 살펴보도록 하겠습니다.
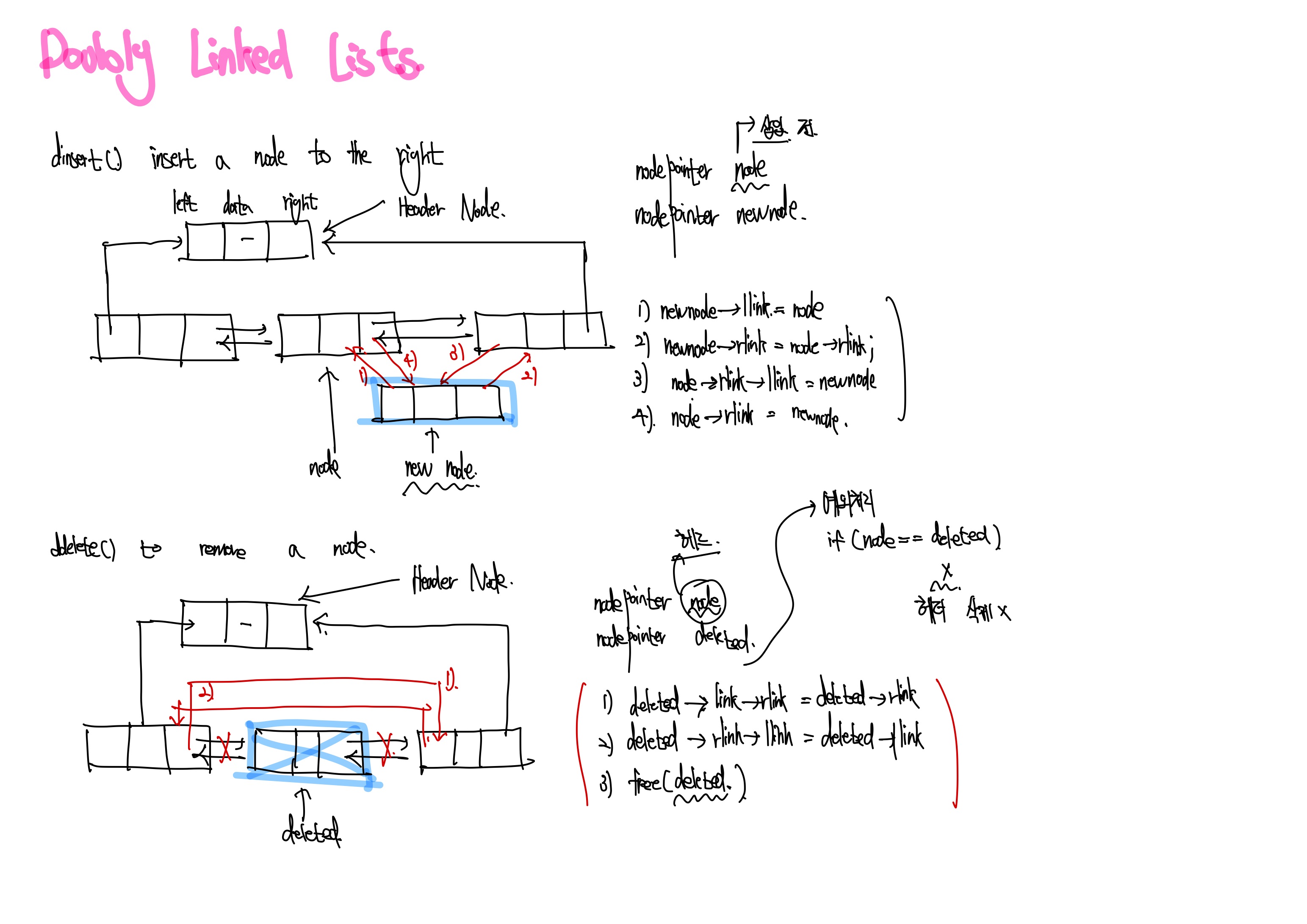
dinsert
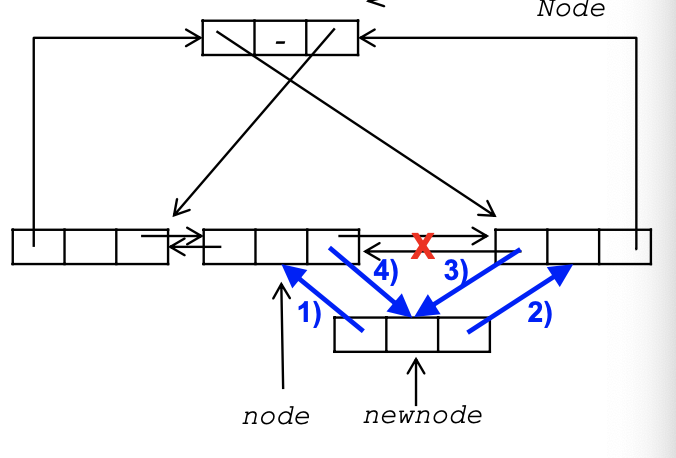
dinsert의 기본 연산의 원리에 대해서 살펴보도록 하겠습니다. 일단 인자로는 삽입하기 전 node를 가리키는 포인터와, 삽입할 node포인터를 받습니다. 이제 삽입할노드를 newNode라고 하고 전노드를 node라고 합시다. 그럼 newnode->llink = node를 한 후, newnode->rlink = node-rlink를 하고, node->rlink->llink = newnode를 하고 마지막으로 node->rlink = newnode를 하면 newnode를 node후에 삽입하게 됩니다.
ddelete
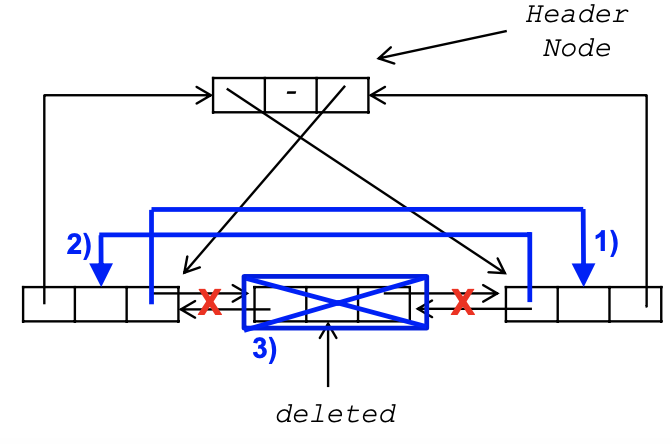
ddelete의 기본 연산의 원리에 대해서 살펴보도록 하겠습니다. 일단 인자로는 headernode인 node와 삭제할 노드포인터인 deleted를 받게 됩니다. 그리고 deleted->llink->rlink = deleted->rlin를 하고 deleted->rlink->llink = deleted->llink를 한 후 마지막으로 free(deleted)로 해재해 주고 마지막으로 node가 deleted라면 에러 메세지를 띄우면 끝내면 됩니다. 그러면 성공적으로 deleted에 해당하는 노드가 삭제됩니다.
doubly-linked-list 총 정리
'School > DataStructure' 카테고리의 다른 글
| Data-Structure - Arrays and Structure (0) | 2022.04.16 |
|---|---|
| Data-Structure - Tree (0) | 2022.04.14 |
| Data-Structure - Linked-List( Application - 2 ) (0) | 2022.04.08 |
| Data-Structure - Linked list ( Applications ) (0) | 2022.04.05 |
| Data-Structure - Linked Lists (0) | 2022.04.01 |
