Polynomials

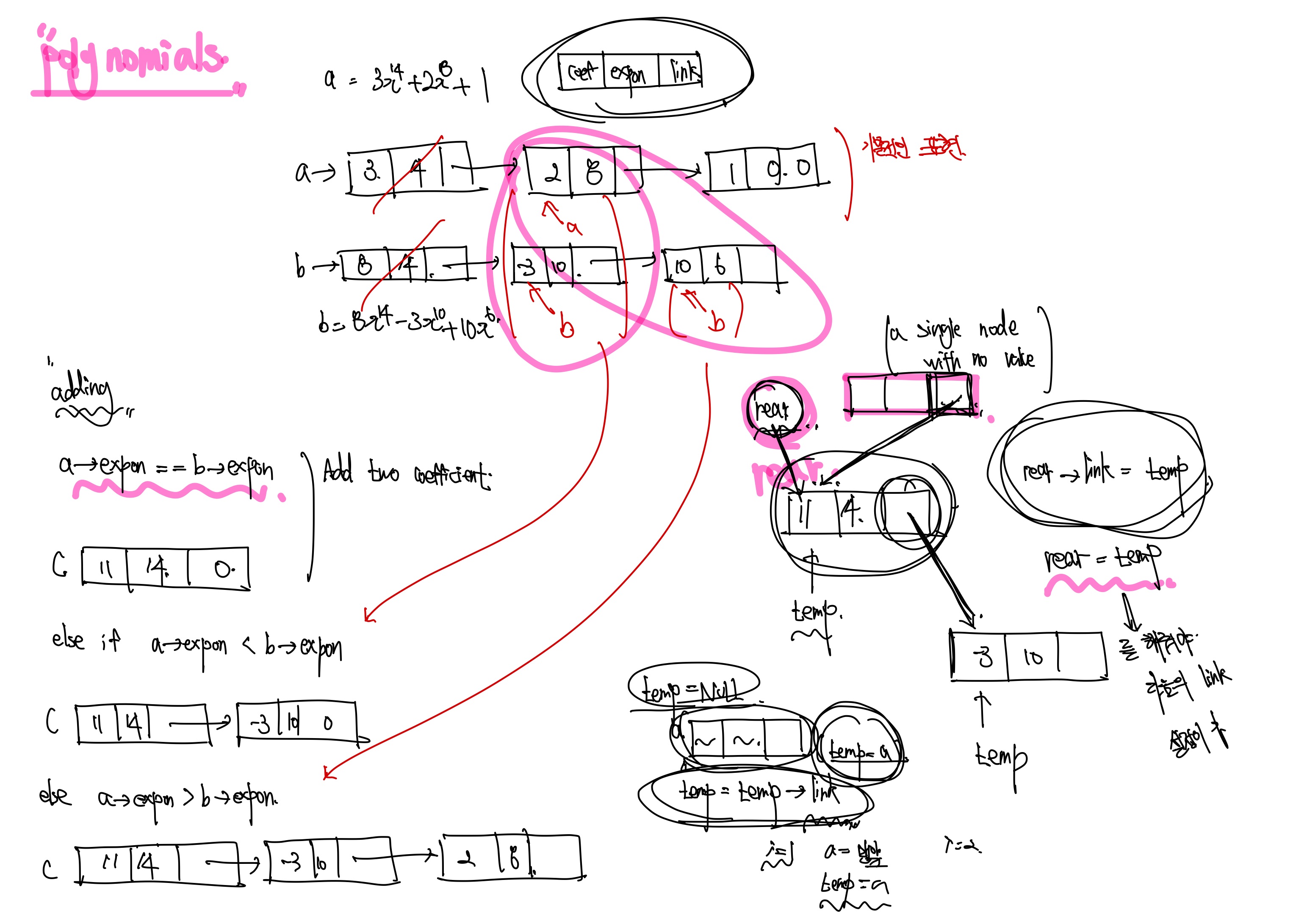
우리는 다음과 같은 polynomials를 구조체를 통해서 구현을 했었습니다. 근데 이는 linked-list를 통해서도 더욱 효율적이고 간편하게 만들 수 있습니다.

바로 이렇게 생긴 구조체와 자기참조 구조체를 통해서 linked-list를 구현하면 됩니다. data칸에 float형 coef(계수)와 int형 expon(지수)를 넣고 다음 linked-list를 가리킬 link를 만들어 주면 됩니다. 간단합니다!!

각각의 a, b다항식을 위와같이 linked-list로 표현을 해 주었습니다.

기본적인 추가 규칙은 구조체를 활용해서 간단히 구현했을때와 다른것이 없습니다. 그냥 expon(지수)를 비교해서 각각의 경우에 다르게 처리해 주면 끝입니다. 하지만 linked-list답게 포인터를 연결하는 부분이 어렵다고 느껴질 뿐입니다.

또한 위 그림처럼 새로운 linked-list를 구현해 갑니다. 새로 추가할 노드를 temp로 만들고 rear를 계속 link해가면서 추가하는 방식입니다. 그림을 보고 이해해가면 그렇게 어렵지 않습니다.
이제 제가 구현한 코드를 보겠습니다.
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_QUEUES 10 /* maximum number of stacks */ #define ERROR_KEY -100 #define MALLOC(p, s) \ if (!((p) = malloc(s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } #define REALLOC(p, s) \ if (!((p) = realloc(p, s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } typedef struct polyNode { float coef; int expon; struct polyNode *link; } * polyPointer; polyPointer a, b; int COMPARE(int expon1, int expon2) { if (expon1 < expon2) return -1; else if (expon1 > expon2) return 1; else return 0; } void attach(float coefficient, int exponent, polyPointer *ptr) { /* create a new node with coef = coefficient and expon = exponent, attach it to the node point to by ptr. */ polyPointer temp; MALLOC(temp, sizeof(*temp)); temp->coef = coefficient; temp->expon = exponent; (*ptr)->link = temp; *ptr = temp; } polyPointer padd(polyPointer a, polyPointer b) { /* return a polynomial which is the sum of a and b */ float sum; polyPointer c, rear, temp; MALLOC(rear, sizeof(*rear)); c = rear; while (a && b) { switch (COMPARE(a->expon, b->expon)) { case -1: attach(b->coef, b->expon, &rear); b = b->link; break; case 0: sum = a->coef + b->coef; if (sum) { attach(sum, a->expon, &rear); } a = a->link; b = b->link; break; case 1: attach(a->coef, a->expon, &rear); a = a->link; break; } } /* copy rest of list a and then list b */ for (; a; a = a->link) attach(a->coef, a->expon, &rear); for (; b; b = b->link) attach(b->coef, b->expon, &rear); /* delete extra initial node */ temp = c; c = c->link; free(temp); return c; } void insert(polyPointer *first, polyPointer x, float coef, int expon) { polyPointer temp; MALLOC(temp, sizeof(*temp)); temp->coef = coef; temp->expon = expon; if (*first) { temp->link = x->link; x->link = temp; } else { temp->link = NULL; *first = temp; } } void printList(polyPointer first) { printf("The list contains: "); for (; first; first = first->link) { if (first->expon != 0) { if (first->link == NULL) { printf("%.2fx^%d", first->coef, first->expon); putchar('\n'); return; } printf("%.2fx^%d + ", first->coef, first->expon); } else { printf("%.2f", first->coef); putchar('\n'); return; } } printf("\n"); } void readPolynomial(polyPointer *pPoint, FILE *fp_read) { int i, number, expon; float coef; polyPointer temp = NULL; fscanf(fp_read, "%d", &number); for (i = 0; i < number; i++) { fscanf(fp_read, "%f %d", &coef, &expon); insert(pPoint, temp, coef, expon); if (i == 0) { temp = *pPoint; } else { temp = temp->link; } } } int main(void) { FILE *fp_read; fp_read = fopen("a.txt", "r"); polyPointer a = NULL; readPolynomial(&a, fp_read); polyPointer b = NULL; fp_read = fopen("b.txt", "r"); readPolynomial(&b, fp_read); fclose(fp_read); printList(padd(a, b)); return 0; }
메인 c언어 파일은 위와 같고 a.txt와 b.txt는 아래와 같게 작성했습니다.
// a.txt 3 3 20 2 5 4 0
// b.txt 4 1 4 10 3 3 2 1 0
a.txt와 b.txt의 기본 작성 방식은 처음에는 (계수, 지수)의 순서쌍의 계수가 나오고 가 다음으로는 처음에 받은 숫자만큼의 (계수, 지수)순서쌍이 나오게 됩니다.

이에 대한 결과는 위와 같은데 a.txt의 다항식과 b.txt의 다항식이 적절한 형식에 따라 계수는 float형식으로 잘 출력이 된 것을 볼 수 있습니다.
또한 출력을 한 다음에 polynomails이 차지하는 메모리 공간을 해제해 주려면 다음과 같이 하면 됩니다.
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_QUEUES 10 /* maximum number of stacks */ #define ERROR_KEY -100 #define MALLOC(p, s) \ if (!((p) = malloc(s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } #define REALLOC(p, s) \ if (!((p) = realloc(p, s))) \ { \ fprintf(stderr, "Insufficient memory"); \ exit(EXIT_FAILURE); \ } typedef struct polyNode { float coef; int expon; struct polyNode *link; } * polyPointer; polyPointer a, b; int COMPARE(int expon1, int expon2) { if (expon1 < expon2) return -1; else if (expon1 > expon2) return 1; else return 0; } void attach(float coefficient, int exponent, polyPointer *ptr) { /* create a new node with coef = coefficient and expon = exponent, attach it to the node point to by ptr. */ polyPointer temp; MALLOC(temp, sizeof(*temp)); temp->coef = coefficient; temp->expon = exponent; (*ptr)->link = temp; *ptr = temp; } polyPointer padd(polyPointer a, polyPointer b) { /* return a polynomial which is the sum of a and b */ float sum; polyPointer c, rear, temp; MALLOC(rear, sizeof(*rear)); c = rear; while (a && b) { switch (COMPARE(a->expon, b->expon)) { case -1: attach(b->coef, b->expon, &rear); b = b->link; break; case 0: sum = a->coef + b->coef; if (sum) { attach(sum, a->expon, &rear); } a = a->link; b = b->link; break; case 1: attach(a->coef, a->expon, &rear); a = a->link; break; } } /* copy rest of list a and then list b */ for (; a; a = a->link) attach(a->coef, a->expon, &rear); for (; b; b = b->link) attach(b->coef, b->expon, &rear); /* delete extra initial node */ temp = c; c = c->link; free(temp); return c; } void insert(polyPointer *first, polyPointer x, float coef, int expon) { polyPointer temp; MALLOC(temp, sizeof(*temp)); temp->coef = coef; temp->expon = expon; if (*first) { temp->link = x->link; x->link = temp; } else { temp->link = NULL; *first = temp; } } void printList(polyPointer first) { printf("The list contains: "); for (; first; first = first->link) { if (first->expon != 0) { if (first->link == NULL) { printf("%.2fx^%d", first->coef, first->expon); putchar('\n'); return; } printf("%.2fx^%d + ", first->coef, first->expon); } else { printf("%.2f", first->coef); putchar('\n'); return; } } printf("\n"); } void readPolynomial(polyPointer *pPoint, FILE *fp_read) { int i, number, expon; float coef; polyPointer temp = NULL; fscanf(fp_read, "%d", &number); for (i = 0; i < number; i++) { fscanf(fp_read, "%f %d", &coef, &expon); insert(pPoint, temp, coef, expon); if (i == 0) { temp = *pPoint; } else { temp = temp->link; } } } void erase(polyPointer *ptr) { /* erase the polynomial pointed to by ptr */ polyPointer temp; while (*ptr) { temp = *ptr; *ptr = (*ptr)->link; free(temp); } } int main(void) { FILE *fp_read; fp_read = fopen("a.txt", "r"); polyPointer a = NULL; readPolynomial(&a, fp_read); polyPointer b = NULL; fp_read = fopen("b.txt", "r"); readPolynomial(&b, fp_read); fclose(fp_read); polyPointer resultPolynomial = padd(a, b); printList(resultPolynomial); erase(&resultPolynomial); return 0; }
linked-list Polynomial 정리
Circular List Representation of Polynomials
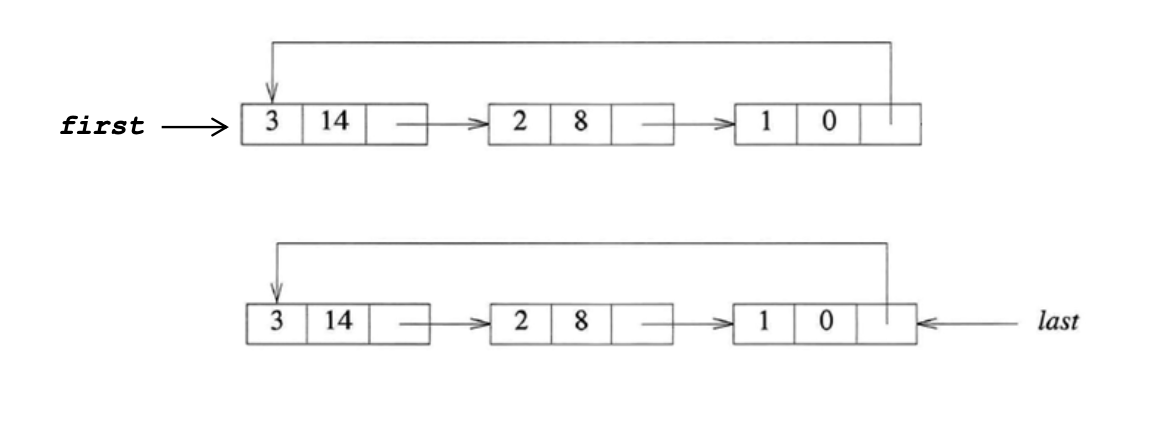
또한 우리는 위에서 Linear-List(Chain)형태로 Polynomials를 구현하였습니다. 하지만 마지막 노드가 맨 처음 노드를 가리키도록 함 으로써 Circular-List형태로 Polynomials를 구현할 수 있습니다.
'School > DataStructure' 카테고리의 다른 글
| Data-Structure - Linked-List ( Application - 3 ) (0) | 2022.04.08 |
|---|---|
| Data-Structure - Linked-List( Application - 2 ) (0) | 2022.04.08 |
| Data-Structure - Linked Lists (0) | 2022.04.01 |
| Data-Structure - Circular Queues (0) | 2022.04.01 |
| Data-Structure - Queue (0) | 2022.04.01 |
