![[ 딥러닝 최신 알고리즘 - PRMI Lab ] - Generative model + Embedding (WaveNet., PixelCNN++, Self-Attention, Auto-Encoder, Bag, Word2Vec)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FkMfJM%2FbtspE3MB24B%2Fgj55UT1JTuFFSFZAAShffK%2Fimg.png)
이번에는 트랜스포머를 구현하기 전에, 최종적으로 개념 정리를 하려고 합니다. 먼저 개념을 간단히 훑겠습니다.
Auto-encoder
오토인코더(Auto-Encoder)는 신경망의 한 종류로, 비지도 학습 방법에 속합니다. 입력 데이터의 압축된 표현을 학습하고, 이를 다시 입력 데이터와 같은 크기로 복구해내는 것이 목표입니다.
대표적으로 U-net이 있고, DeConvNet도 예로 들 수 있습니다. 이는 입력 데이터의 압축된 표현을 학습하면서, 그 표현을 이용해 원본 입력 데이터를 재구성하는 능력을 취득하게 됩니다. 이렇게 학습된 오토인코더는 차원 축소, 노이즈 제거, 특성 추출 등 다양한 용도로 활용될 수 있게 됩니다.
Sequence-to-Sequence에서의 임베딩(embedding)
위와같이 seq2seq모델은 인코더(encoder)와 디코더(decoder)로 구성되어 있으며, 본 논문에서는 아래와 같이 각각의 역할을 정리할 수 있습니다.
- Encoder: 입력 값의 정보를 받아 latent variable (잠재 변수 혹은 context vector)로 embedding(압축)하는 단계
- Decoder: 인코더의 context 값과 이전까지의 값을 받아, auto-regressive하게 분포를 "생성"하는 단계
임베딩(embedding)이란?
그럼 seq2seq에서 사용되는 임베딩은 뭘까요? 이는 모집단의 성격을 보존하면서도 모집단과는 다른 형태의 소집단으로 매핑(mapping)되는 것입니다. 즉 Dimension reduction 방법등을 통해 얻어질 수 있습니다. 크게 3가지 용도로 사용됩니다.
- 가장 가까운 이웃 정보를 찾도록 해준다 -> 유저의 관심사나 클러스터 카테고리에 대해서 추천을 하도록 도와준다.
- 머신 러닝의 피처로서 learning을 위한 입력 값을 임베딩하여 사용할 수 있다.
- 카테고리 간 개념과 관련 정도를 시각화 해줄 수 있다.
자가회귀(Auto-regressive) 모델이란?
말 그대로 시퀀스에서 time stamp t를 예측한다면 우리는 $x_{1} ~ x_{t-1}$까지의 정보를 이용할 수 있을겁니다. 즉 아래와 같이 순차적으로 예측할 수 있습니다.
이런 모델을 "자가 회귀"모델이라고 합니다.
생성 모델(generative model)이란?
즉 최종적으로 생성 모델이란 $p_{data}(x)$와 유사한 $p_{model}(x)$를 학습하는 것을 말합니다. 이를 통해 원하는 이미지를 복구하거나 새 샘플을 만들어 낼 수 있게 됩니다.!
즉 위에서 보았던 Auto-regressive, autoencoder, sequence-to-sequence는 생성 모델의 일종이라 볼 수 있습니다. Embeddimg의 경우, dimension reduction과 가까우며, 위의 생성모델의 성능 향상을 위한 기반 연구로써 많이 쓰이게 됩니다.
생성 모델의 종류
- Implicit density emstimation
- 이는 $p_{model}(x)$를 직접 구하지 않아도, 게임이론 같이 경쟁을 시켜서 샘플을 생성할 수 있습니다.
- GAN, GSN같은게 이에 속합니다. -> 추후 포스팅 예정
- Explicit density estimation
- $p_{model}(x)$를 구하기 위해 loss등에 직접 반영하고 최적화 합니다.
- 지금은 본 방법을 위주로 집중적으로 보도록 하겠습니다.
자동 회귀 Auto-regressive의 예시
RNN등의 recurrent 모델을 이용하는 방법
먼저 RNN등의 recurrent 모델을 이용하는 방법입니다. 하지만 이는 병렬 컴퓨팅이 너무 어렵습니다. 이는 teacher_forcing으로 seq2seq모델에서 성능을 끌어 올렸던 것을 보았습니다. 이가 decoder에서 병렬적으로 계산되게 돕지만 근본적으로 해결할 수는 없습니다.
Masking을 이용하는 방법
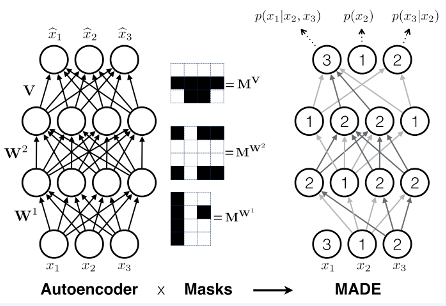
이는 Masked MLP, convolutions, self-attention에 사용되는 기법입니다. 동일 시간상의 연산들끼리 병렬 컴퓨팅이 가능하게끔 하고, 이전 계산 값이 쓰이지 않는다면, 이 역시 계산가능합니다. 이는 파라미터들이 시간이 지남에 따라 공유되게됩니다.
사실 transformer에서 self-attention에 위 개념이 매우 중요하게 쓰이게 됩니다. 위 그림을 보면 이해가 쉬울겁니다. 말 그대로 시간이 지남에 따라 보이는 영역(=참고할 수 있는 영역)이 증가한다고 보면 되겠습니다.
이를 위해서 참고로 upper_triangle_matrix를 사용해서 MATMUL(x, param * mask)를 통해 autogressive의 결과를 뱉어낼 수 있습니다.
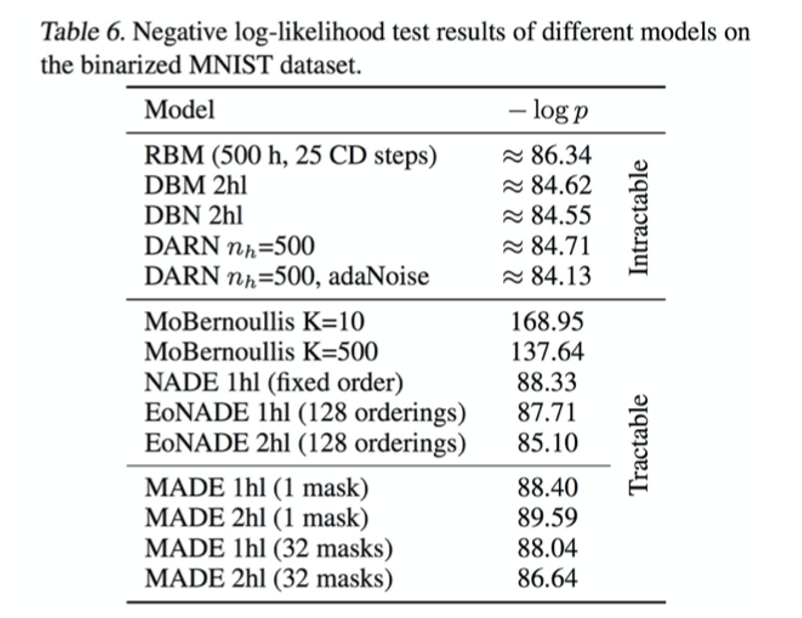
당시에 그래서 2015년에 Deep Botlzman Machine보다 더 성능이 좋은 생성 모델을 만들 수 있었다고 합니다.
Masked Temporal (1D) Convolution
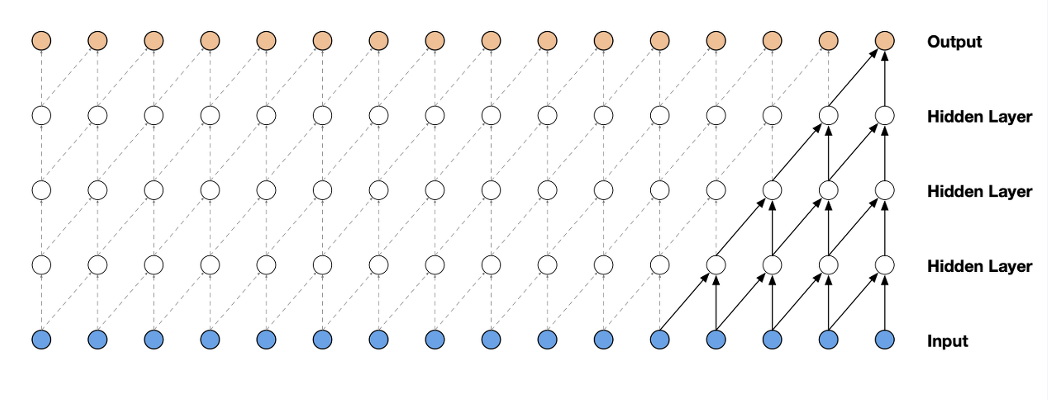
위와같이 합성곱 신경망 convolutional layer의 kernel(receptive field)에 masking part의 구현을 위에서 볼 수 있습니다.
이는 MLP에 마스킹을 통해서 CNN을 구현한것인데, 이렇게 하면 단순 마스킹을 사용하기 때문에, 구현하기가 훨씬 쉽습니다. 또한 큰 크기라 하더라도 파라미터 수가 CNN과 같이 shared weight를 통해 유지가 됩니다. 또한, CNN자체가 GPU등에서 이미 많이 최적화가 되어있어, computation cost적인 측면에서 효율적입니다.
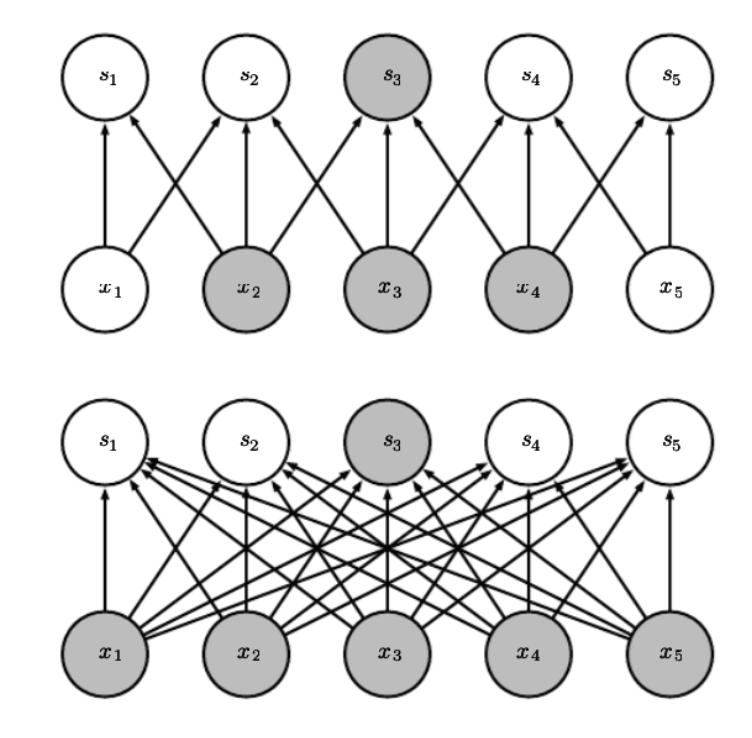
위와같이 CNN은 파라미터를 공유해서 연산을 효율적으로 수행하고, sparse하게 뉴런을 만들어서 피처 벡터도 잘 추출할 수 있게됩니다.
하지만 이는 receptive field에 제약을 거는 것이라 그 자체로는 한계가 존재합니다. (layer의 수에따라 linear하게 증가한다..!)
WaveNet (2016)
receptive field가 linear하게 증가한다는 제약을 어느정도 해결하기 위해. WaveNet에서는 receptive field를 dilated convolution으로 보완했습니다. 이는 선형적으로 증가하는 것이 아닌, exponential한 dilation입니다.
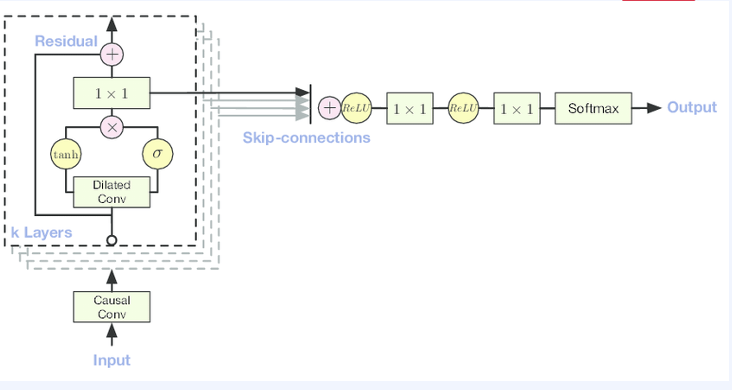
또한 WaveNet에서는 그당시에 ResNet이 등장했던 시기여서 Gated residual block, skip connection을 사용해서 성능을 극대화 했었습니다. 이는 오디오 분야에서 매우 유명한 모델입니다.
Masked Temporal (2D) Convolution
Computer Vision에서의 이미지 분류와 같은 분야는 거의 data와 label의 관계를 이용해 예측하는 식이었습니다. 하지만, label이 없는 상황에서 training sample의 분포를 예측해 내는 것의 Generative는 Density Modeling(밀도 기반 모델링)이라고 합니다.
결론적으로 픽셀을 생성하는 과정에서 각 픽셀값의 정답(Ground Truth)를 가지고 있을텐데 이러한 과정의 likelihood를 최대화하는 것과 같습니다. (낮은 likelihood를 가지면 OOD가 될 것이다.)
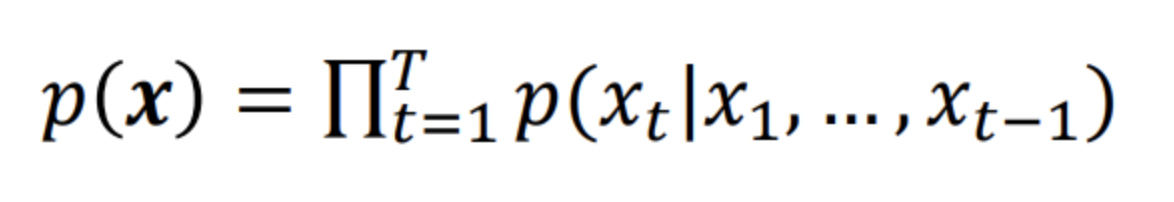
즉 이가 Autogressive인 이유는 자기 자신을 input으로 하여 자기 자신을 예측하는 모델이기 때문입니다.
PixelCNN | Gated PixelCNN (2016)
이는 이미지를 1D로 flatten할 수 있지만, 2D의 spaitial한 정보를 이렇게 하면 잃을 수 있게됩니다. 그래서 2D이미지를 mask하여 order를 지킬 수 있지 않을까? 라는 궁금증에서 구현된 모델입니다. -> (모든 시퀀스를 다 convolution하게 되면 연산량이 너무 많아져서 이를 최소화 하기 위해 mask를 씌운 이유 중 하나기도 함)
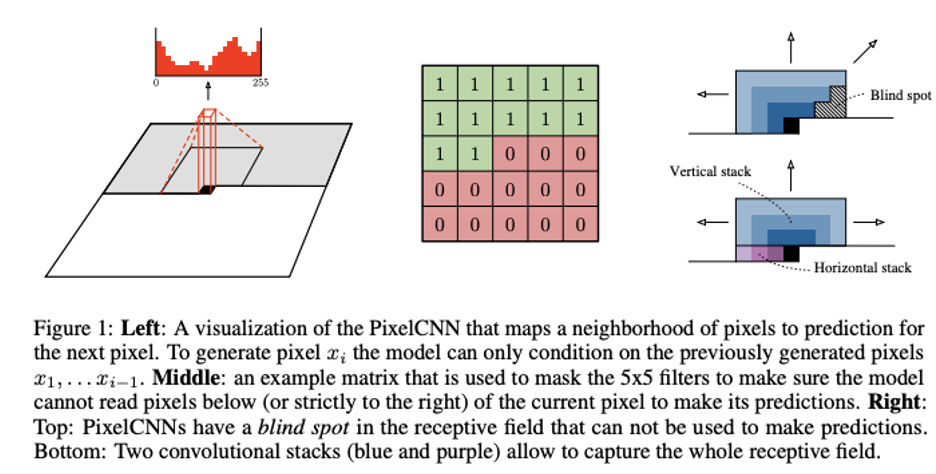
위와같이 Auto-gressive order을 정한 mask를 써서 PixelCNN이 탄생했습니다.
하지만 한가지 문제는 blind spot이 생길 수 있습니다. 이는 오른쪽 그림에서 그 이유를 파악할 수 있습니다. 그래서 Horizontal stack과 Vertical한 부분을 나누고, 두 개의 stream을 결합할 수 있는데, 이를 Gated PixelCNN이라고 합니다.
- Horizontal Stack: 현재 행을 기준으로 조절하여 horizontal stack뿐만 아니라 이전 레이어의 출력도 입력으로 사용합니다.
- Vertical Stack: 현재 픽셀 부분 윗부분의 모든 행(row)에 mask없이 적용합니다. 이 출력물이 horizontal stack에 공급되고 receptive field가 직사각형 형태로 계속 커지게 됩니다.
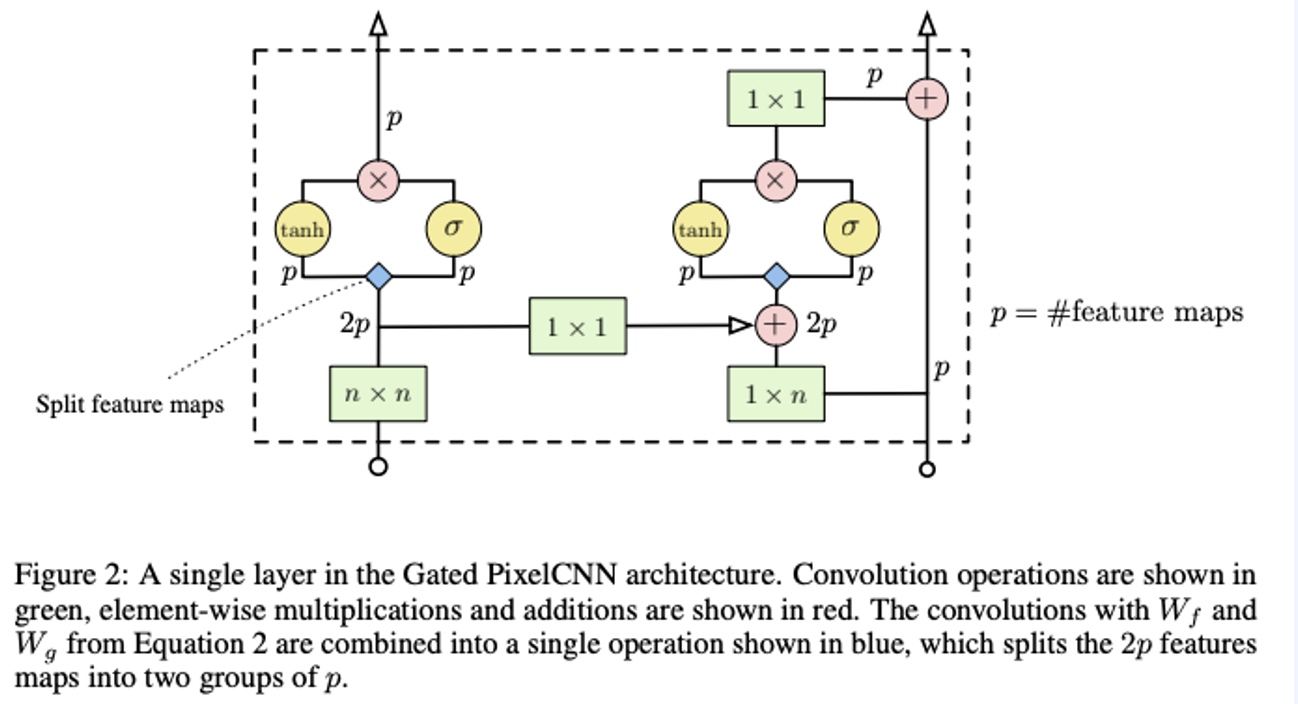
위 이미지는 Gated ConvNet의 layer입니다. feature map을 2개의 p그룹으로 나누고 다른 activation을 취한뒤 결합하는 것을 볼 수 있습니다.
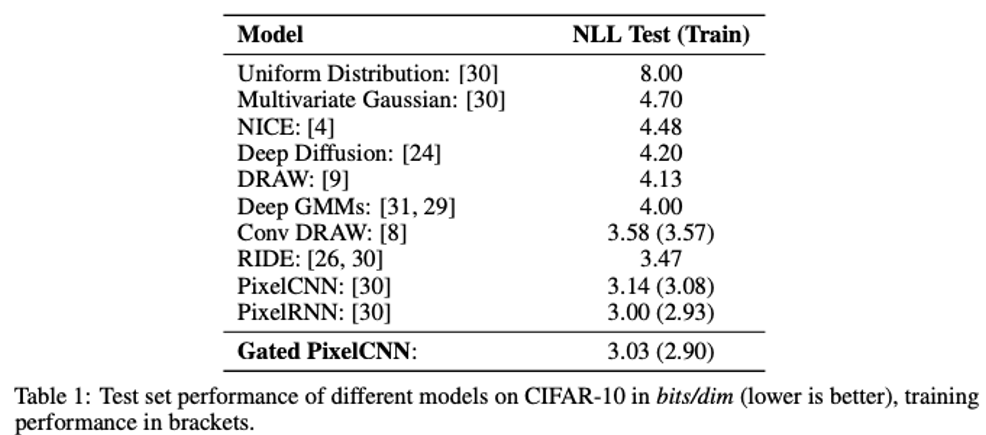
당시에 CNN으로 Generative Model까지 할 수 있겠어? 라는 회의를 깨고 다른 모델을 이긴 아주 획기적인 학회에서 유명한 모델이였다고 합니다.
PixelCNN++ (2017)
하나의 픽셀은 (0~255)의 값을 가지고 RGB라면 x3입니다. 이 모든걸 softmax를 취해서 예측을 PixelCNN에서는 했습니다. 하지만 이는 너무 computational cost적으로 손해입니다. 그리고 이는 gradient를 너무 빠르게 sparse하게 만듭니다. 또한, 이러한 softmax는 비싼데, 우리는 이미 주변의 pixel color intensity값들이 거의 동시에 일어나는 것(co-occur)을 알고 있습니다.
Color intense를 나타내는 것이 discrete한 8bit(2**8=256)이 아닌, 0~255를 추론하는 확률 분포값을 나타낸다고 하여 계산합니다. (variational auto-encoder와 비슷한 아이디어 -> TBD)
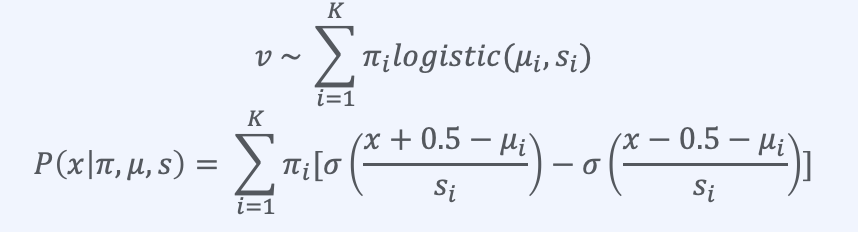
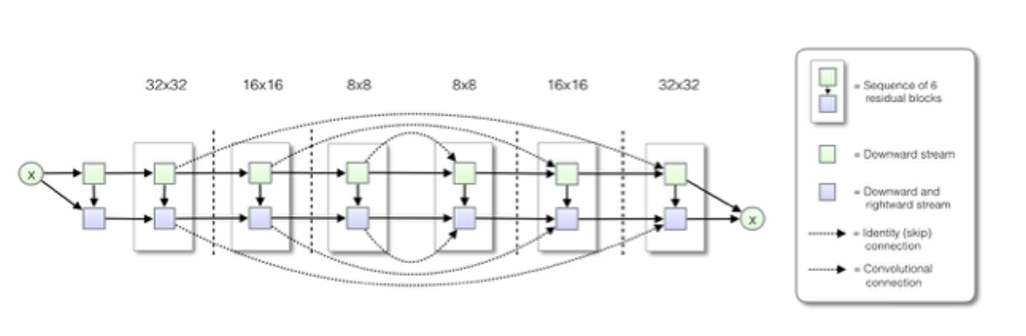
위와같이 평균과 분산을 조정하고 확률 분포값을 바꿔나가는 식으로 돌리게 되는 것이 PixelCNN++입니다. 또한 PixelCNN++에서는 U-Net의 장점들을 취합니다.
- 다운 샘플링 (down-sampling)
- Pixel CNN은 장거리 종속성을 계선할 수 없었습니다. -> 이를 극복하기 위해 Stride=2의 convolution layer로 다운 샘플링합니다. 다운 샘플링은 입력 크기를 줄여 receptive field의 상대적 크기를 계선하여 정보 손실을 가져오지만, skip-connection을 추가하여 보완할 수 있게됩니다.
- Skip-connection
- U-net과 같이 다운샘플링 & 업샘플링 중 인코더 디코더에 skip-connection을 가지게 됩니다.
Self-attention
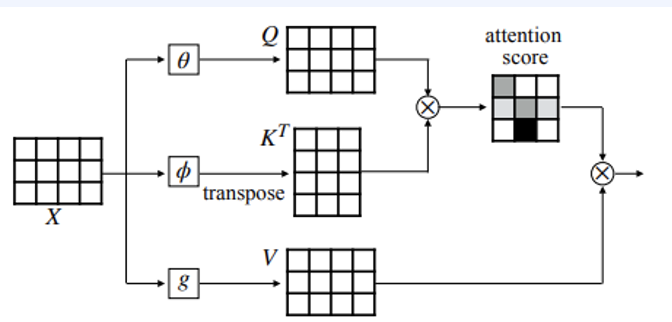
우리가 너무 많이 봤던 self-attention도 결국엔 mask기반입니다. 즉 임베딩된 Q, k, V를 mask를 씌워서 Auto-Regressive하게 바꾸면 되는데, 이게 Transformer의 시작입니다
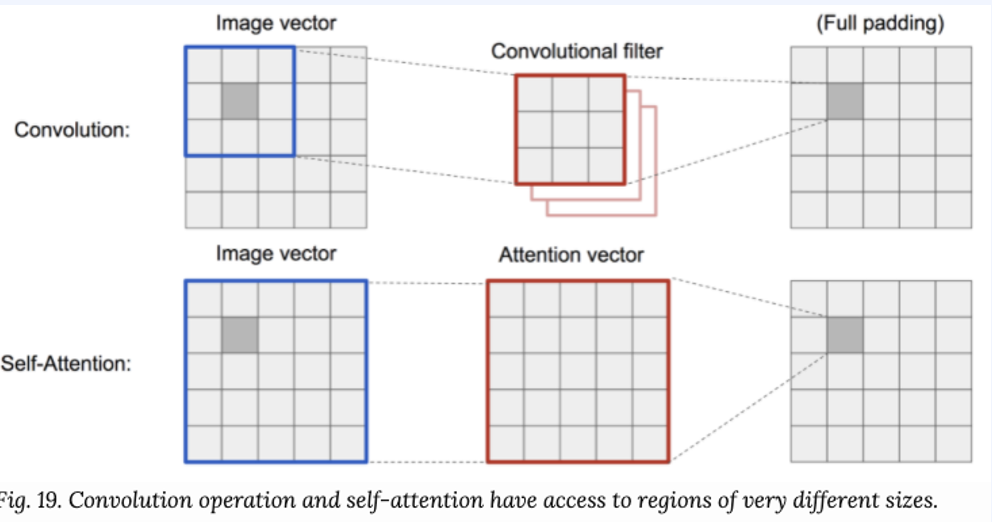
CNN은 receptive field의 크기만큼 볼 수 있다는 단점이 있었다고 수없이 말했습니다. 하지만 self-attention은 무제한의 receptive field, 데이터의 사이즈에 따라 O(n^2) parameter scaling을 가집니다. 또한, RNN등에 비해 parallel computing이 쉬워지게 됩니다.
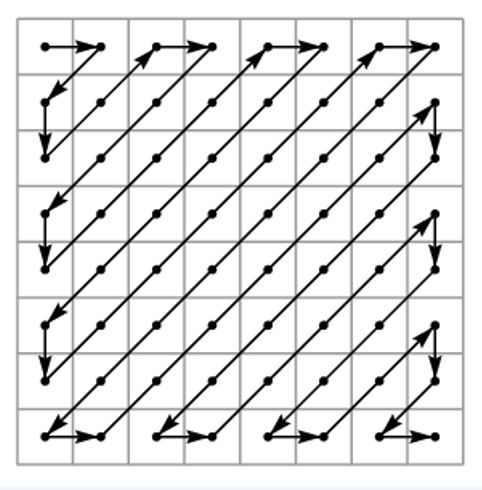
그리고 위와같이 원하는 순서대로 auto-regressive masking이 가능해집니다.
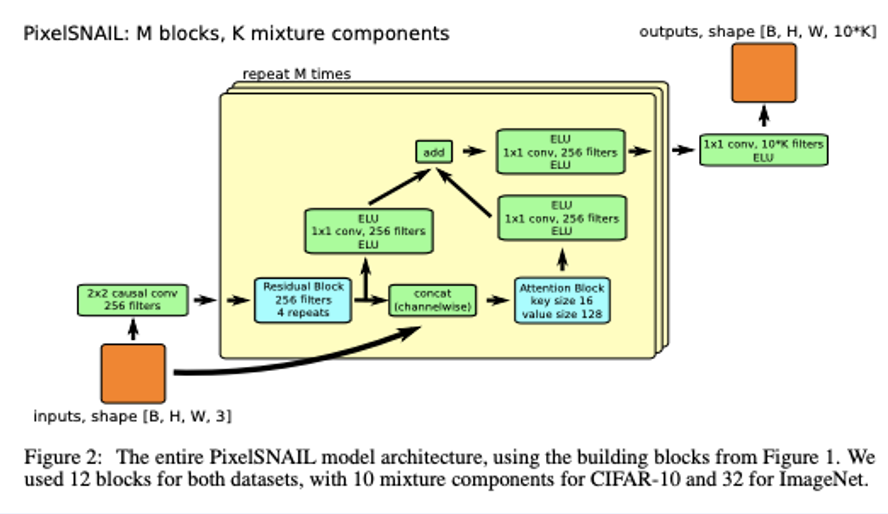
그래서 위와같이 PixelSNAIL (2018)같은게 등장했고, 그 당시에 PixelCNN++를 재치고 SOTA를 찍었다고 합니다.
Applied to "Transformer based models"
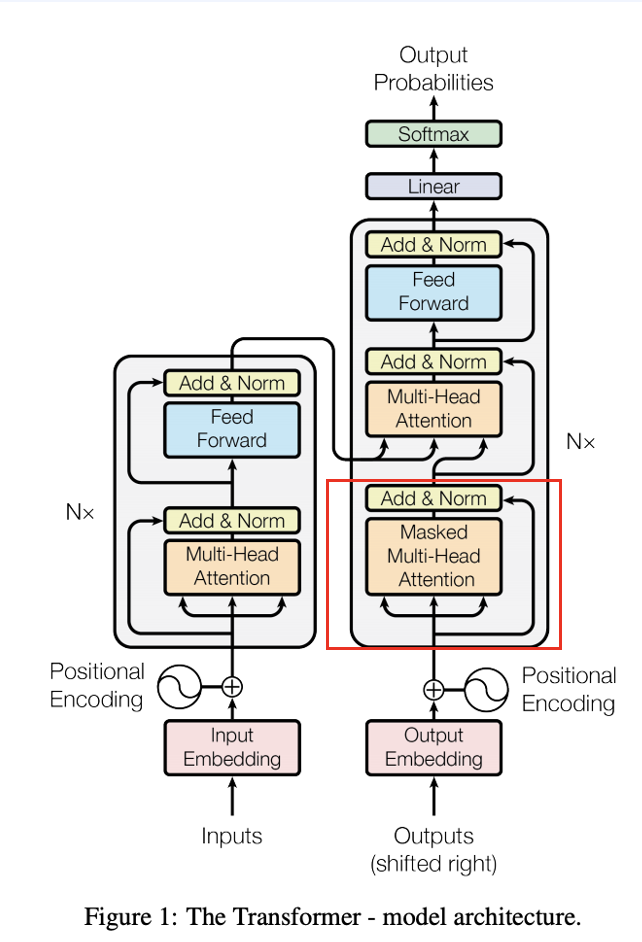
위와같이 encoder-decoder attention에서 이러한 masking attention이 사용되기 때문에, 시간을 내어 알아본 것입니다. 그래서 Neural auto-regressive 모델의 장단점에 대해 간단히 알아보겠습니다.
- 장점
- 모델 성능에 있어 일반적으로 가장 좋습니다.
- 픽셀 단위로 예측을 하기 때문에, GAN과 같은 implicit model이 좋다고 알려져 있음에도. 일반적으로 가장 좋은 것은 Nerual auto-regressive 모델입니다.
- Expressivity: autoregressive factorization이 일반적이고 또 코드를 작성하기 쉬운 편입니다.
- Generalization: 의미있는 parameter sharing이 좋은 귀납적인 편향 (inductive bias)를 주어 일반화가 더 잘됩니다.
- 또한 많은 데이터 셋과 도메인에서 SOTA를 이루게 됩니다.
- 모델 성능에 있어 일반적으로 가장 좋습니다.
- 단점
- 샘플 하나당 한번의 forward pass를 하여야 합니다. -> 여러 forward를 해야할 시.. 매우 느립니다.
- Tesla K40 GPU로 32x32이미지를 생성하면 개당 1분 내외로 걸립니다.
가중치 공유
각 filter의 AlexNet에서 element수는 11x11x3 = 363개입니다.
그리고 각 filter를 거쳐 생성되는 output sizesms (227-11)/4 + 1=55, 즉 55x55x96=290,400개입니다. (96는 필터의 개수를 나타내는 하이퍼파라미터)
따라서 앞서 구한 filter element 개수에 편향 bias까지 고려하여 곱한 총 파라미터 수는 (363 + 1) x 290,400=105,705,600개가 됩니다.
그런데 CNN에서 depth slice간에 같은 가중치를 공유하게 한다면? (같은 feature 위치에서는 같은 특성을 가진다고 하게되면) depth slice당 한개의 파라미터만 필요하므로, 96 x (11 x 11 x 3 + 1)=34,944개만 필요하게 됩니다.
물론 conv layer뿐만 아니라 pooling layer에서도 아예 spatial한 사이즈를 줄여서 파라미터를 줄이기는 합니다. 하지만 풀링의 경우 직접적인 정보 손실이 있는 반면, conv layer는 정보 손실 없이 파라미터를 효과적으로 줄일 수 있다는 장점이 있습니다.
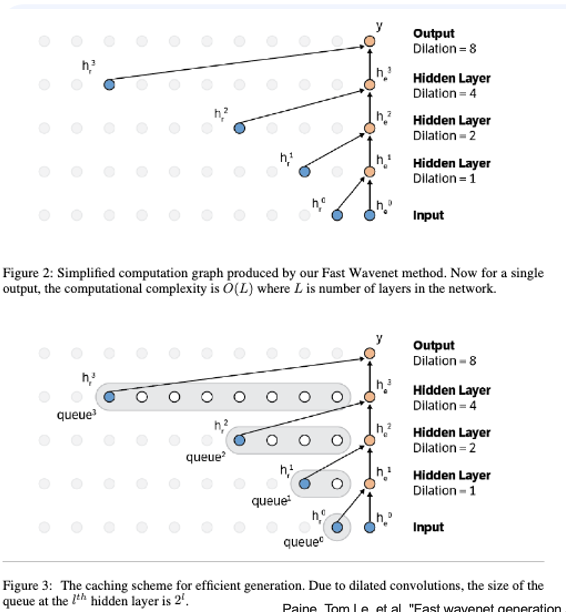
그래서 실제로 Dynamic programming 스럽게 caching을 해서 겹치는 연산을 재사용함으로써 연산을 최소화 할 수 있었다고 합니다. 이는 fast-wavenet, multi-scale PixelCNN에 적용되었습니다. 단, 구현 엔지니어링 난이도가 극악이라고 합니다.
Auto-encoder (오토인코더)
오토 인코더(auto-encoder)는 input을 그대로 output으로 복사하 듯 생성하는 것을 목표로 하는 신경망을 말합니다. 하지만, 이는 훈련과정에서 reconstruction error를 줄이는 것 이상을 의미할 수 있습니다.
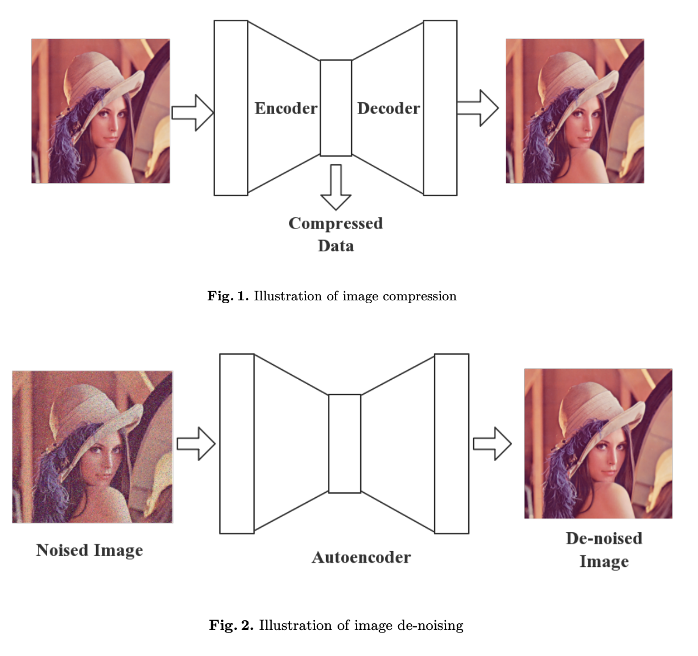
- Embedding
- 중간에 bottle-neck 구조를 취해, 압축된 잠재 변수 (latent variable; latent vector; representation)을 얻기 위한 목적
- Generative model
- 생서물을 원본 대비 의도적인 변형(압축, 노이즈 제거등)이 가해진 출력을 "생성"을 하기 위한 목적
- e.g. denoising auto-encoder
이때, encoder/decoder 함수는 어떠한 함수, network이여도 상관 없습니다.
Vanilla (pure) auto-encoder의 응용 -> Dimension reduction | image restoration
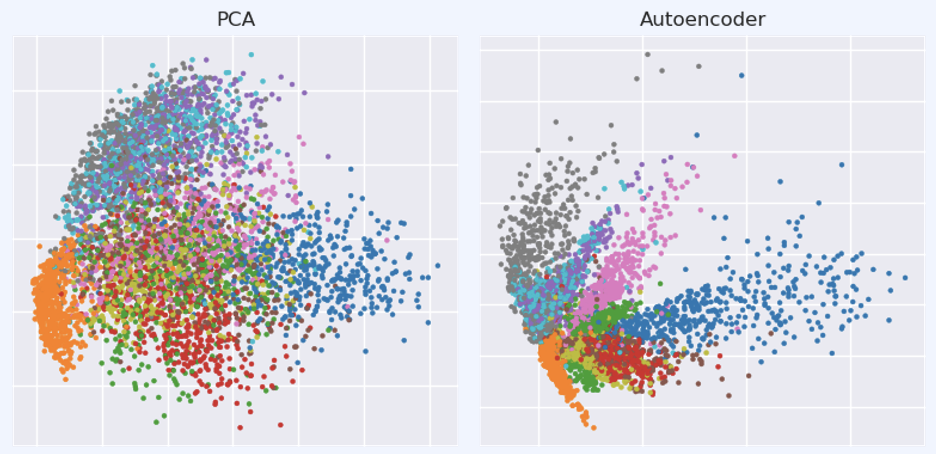
잘 학습된 auto-encoder는 PCA등 기존 ML보다 성능이 좋다고 합니다.
또한 blur한 그림같은걸 auto-encoder를 통해 이미지를 선명하게 복구하는 것처럼 응용할 수도 있습니다.
Embedding
One-hot encoding | Label encoding
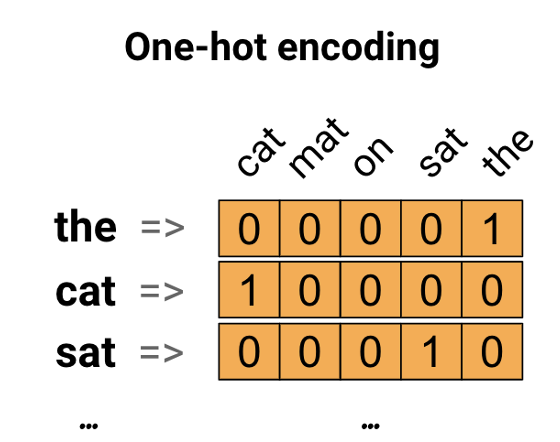
먼저 Label encoding은 고유번호를 integer로 저장하는 방법입니다. [4, 0, 3,...] 이는 간단하고, one-hot에 비해 변환이 빠릅니다. 그리고 멱등성(idempotent)가 보장됩니다.
하지만 각 카테고리의 관계를 파악하기 어렵습니다. e.g. 9-10의 관계는 5-10의 관계보다 가까울 것이라 기대되지만 본 embedding에서는 그렇지 않다. 또한, Loss식 설계 등에서 고려할 점이 늘어나게 됩니다.
그 다음 One-hot encoding은 각 카테고리를 고유번호로 인코딩하고, 번호와 동일한 index에서는 1, 나머지에서는 0을 값으로 하는 벡터로 변환합니다. 이는 매우 간단하고, 각 카테고리가 독립적일 때 매우 유용하지만, 매우 sparse해서 메모리적으로 비효율적입니다. 또한, Label encoding과 비슷하게 카테고리 간 관계를 고려하지 않습니다.
Lookup Table 기반 embedding (torch.nn.Embedding, tf.keras.layers.Embedding)
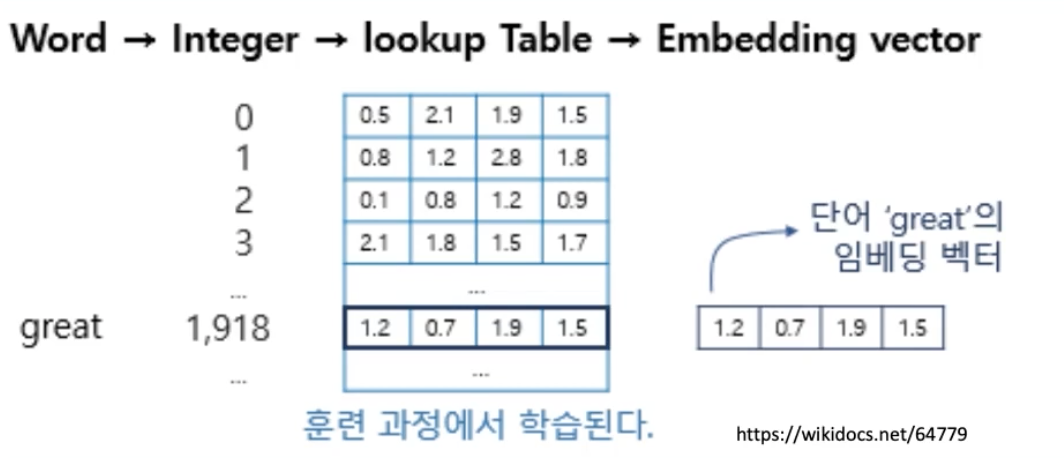
위와같이 integer 카테고리에 1:1로 대응하는 embedding vector를 Table에 모아둡니다. 그리고 Integer를 index로 Table을 Lookup하여 embedding vector를 반환합니다.
이는 또한, 이전에 torch.nn.Embedding을 할떄에도 봤듯이, trainable parameter가 존재합니다. 1:1 대응이기 때문에, 다른 임베딩에 비해 parameter가 단순한 편에 속합니다.
Bag of words기반
bag of words란 문장에서 많이 쓰인 단어를 기반으로 임베딩하는 방식입니다. 주제가 비슷한 문서는 등장하는 단어도 비슷할 것이기 때문이죠. 즉 단어 순서와 상관없이 많이 등장하는 단어는 그 주제와 관련이 있을 것이라는 겁니다. 이러한 전제 하에 단어의 빈도수 자체를 representation으로 사용하는 방식이 bag of words embedding(=bow)입니다.
TF-IDF (Term Frequency - Inverse Document Frequency)
이는 TF와 IDF를 곱한 값을 말합니다. 이는 점수가 높은 단어일수록 다른 문서에는 많지 않고 해당 문서에서 자주 등장하는 단어를 의미합니다.
이의 장점으로는 어떤 단어가 중요한 단어인지 직관적인 해석이 가능하다는 점입니다. 하지만, 문맥에 대한 고려를 해주지 않습니다.
TF) 특정한 단어가 문서 내에 얼마나 자주 등장하는지를 나타냅니다.
DF) 특정 단어가 등장하는 문서의 개수를 말합니다.
IDF) --> log(1/DF)로써 역문서 빈도를 말합니다. -> 이가 크다면 해당 단어가 문서에서 덜 등장하다. 즉 중요하다는 의미가 됩니다.
Latent Semantic Analysis; LSA
기존 one-hot encoding이나 TF-IDF의 "단어의 의미를 고려하지 못하는 단점"을 해결합니다.
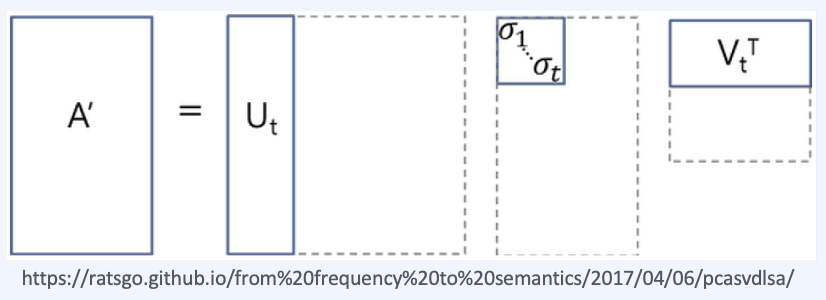
이는 TF-IDF 행렬에 SVD를 적용합니다. 이의 장점으로써는 단어의 잠재적인 의미를 고려할 수 있었다는 점이고, 단점으로는 새로운 정보에 대한 업데이트가 어렵고 단어-문서 간의 similarity를 계산하기 어렵습니다. (차원이 축소되었기 때문)
Pointwise metual information (PMI)
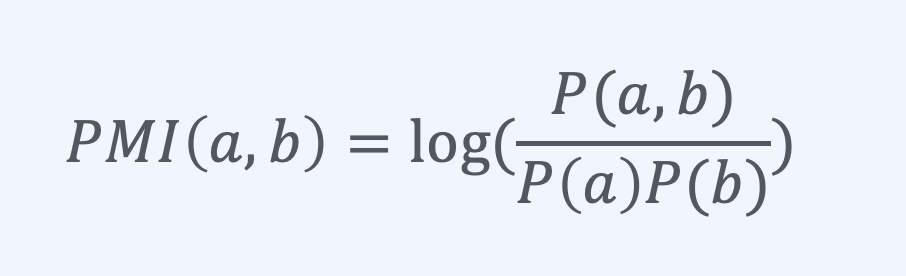
bow기반의 마지막입니다. 이는 정보 이론의 PMI를 이용해서, 각 word간 semantic representation알아내는 방법입니다. TF-IDF와 같이 sparse vector representation방법중에 하나이며, 값이 클수록 correlated되었다는 의미입니다.
신경망 이용: Word2Vec
앞서 one-hot vector는 단어간의 유사성을 계산하지 못한다는 단점이 있음을 언급했습니다. 그래서 단어 벡터간 유의미한 유사도를 반영할 수 있도록 단어의 의미를 수치화할 수 있는 방법이 필요한데, 이를 위해서 사용되는 대표적인 방법이 워드투벡터(Word2Vec)입니다.
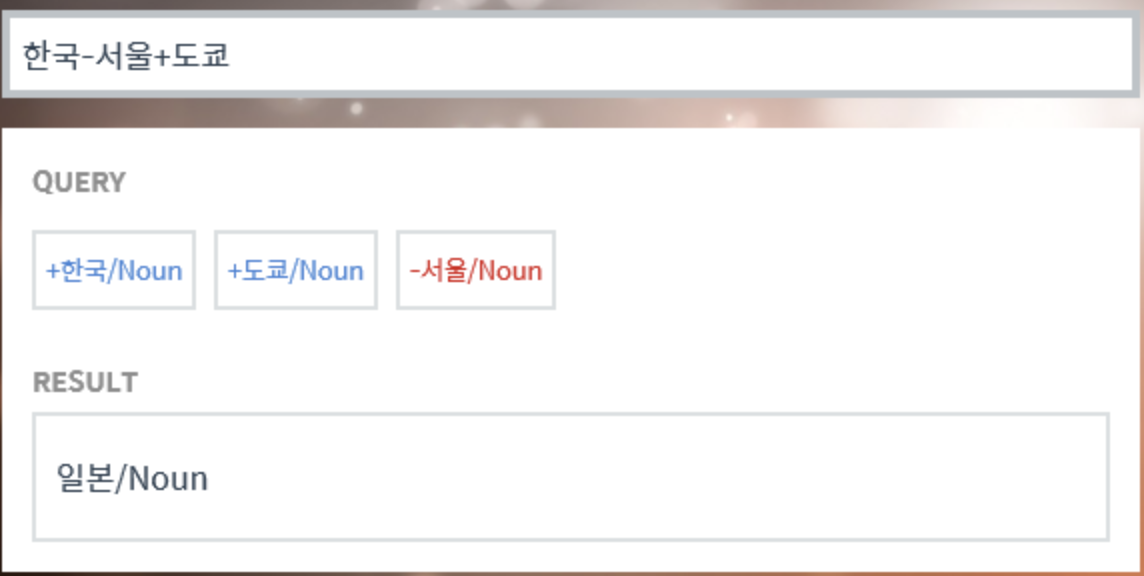
위와같이 word2vec을 사용하면 한국어 단어에 대해서 벡터 연산을 해볼 수 있습니다. 이러한 연산이 가능한 이유는 각 단어 벡터가 단어 벡터 간 유사도를 반영한 값을 가지고 있기 때문입니다.
CBOW(Continuous Bag of Words)
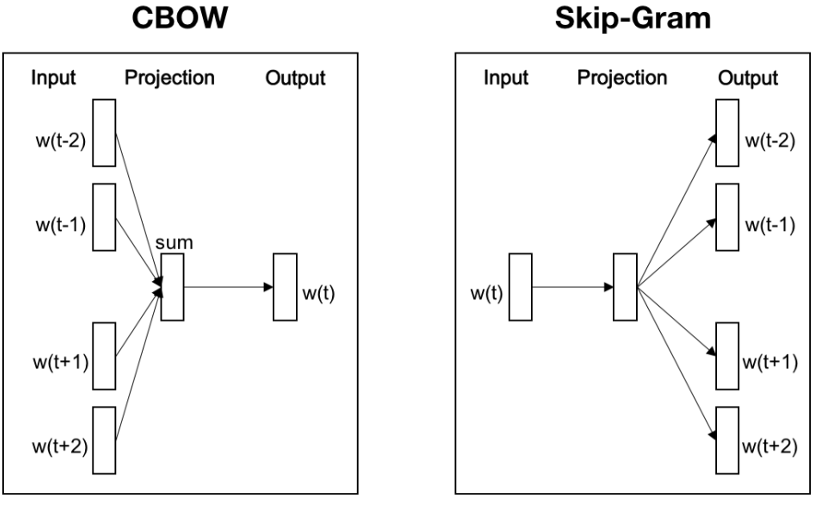
Word2Vec의 학습 방법에는 CBOW, Skip-Gram 2가지 방법이 있습니다. CBOW는 주변에 있는 단어들을 입력으로 중간에 있는 단어들을 예측하는 방법이고, 반대로 Skip-Gram은 중간에 있는 단어를 입력으로 주변 단어들을 예측하는 방법입니다.
매우 간소화된 예시로 설명하겠습니다.
예시) "The fat cat sat on the mat"
갖고 있는 코퍼스에 위와같은 예문이 있다고 하겠습니다. ["The", "fat", "cat", "on", "the", "mat"]으로부터 sat을 예측하는 것이 CBOW가 하는 일입니다. sat을 여기서 중심 단어(center word)라고 하고 예측에 사용되는 단어들을 주변 단어(context word)라고 합니다.
중심 단어를 예측하기 위해서는 앞,뒤로 몇개의 단어를 볼지를 결정해야 하는데 이 범위를 윈도우(window)라고 합니다. 예를 들어 윈도우의 크기가 2이고, 예측하고자 하는 중심 단어가 sat이라고 한다면 앞의 두 단어인 fat와 cat, 그리고 뒤의 두 단어인 on, the를 입력으로 사용합니다.
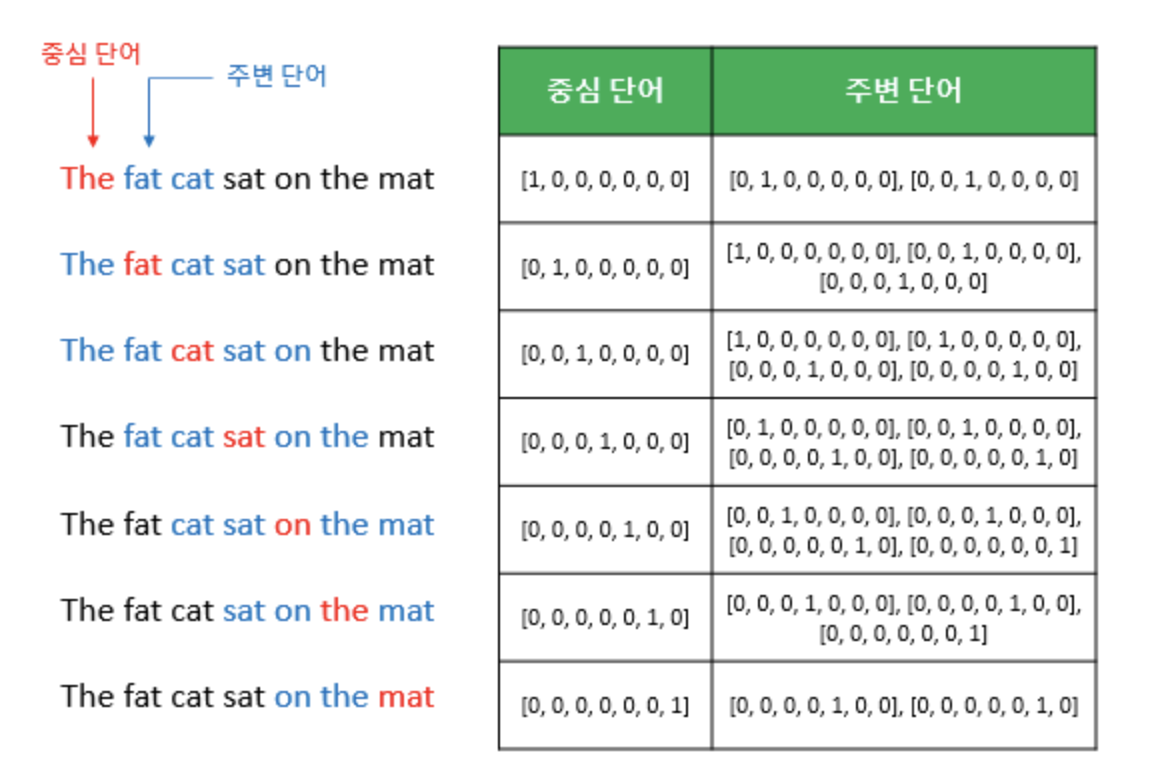
윈도우 크기가 정해지면 윈도우를 옆으로 위와같이 움직여 주변 단어와 중심 단어의 선택을 변경해가며 학습을 뒤한 데이터 셋을 만드는데 이 방법을 슬라이딩 윈도우(sliding window)라고 합니다. Word2Vec에서 입력은 모두 one-hot vector가 되는 것을 위의 예시에서 볼 수 있습니다.
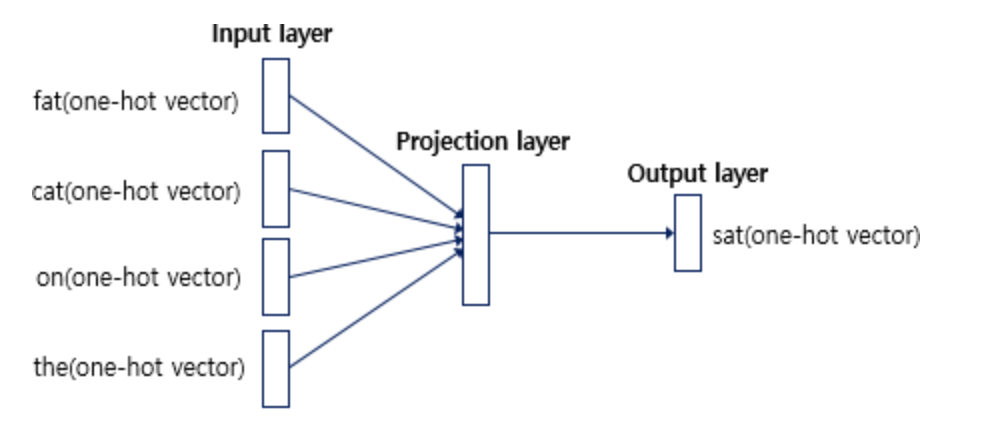
인공신경망을 도식화하면 위와같습니다. 출력층으로 예측하고자 하는 중간 단어의 one-hot vector가 레이블로서 필요합니다. 그리고 위 그림에서 알 수 있는 점은 Word2Vec가 은닉층이 다수인 딥러닝 모델이 아니라 은닉층이 1개인 얕은 신경망(shallow nerual network)이라는 점입니다. 또한 Word2Vec의 은닉층은 일반적인 은닉층과는 달리 활성화 함수가 존재하지 않으며 look-up table이라는 연산을 담당하는 층으로 투사층(projection layer)라고 부르기도 합니다.
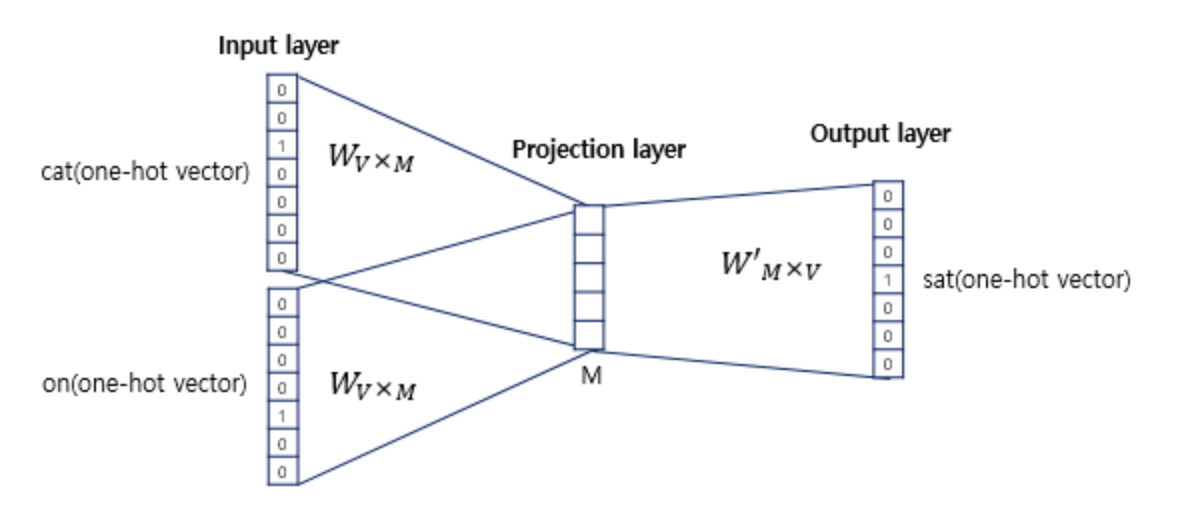
투사층의 크기는 M입니다. CBOW에서 투사층의 크기 M은 임베딩하고 난 벡터의 차원입니다. 위 그림에서 M=5이므로 CBOW를 수행하고 나서 얻는 각 단어의 임베딩 벡터의 차원은 5가 될것입니다.
두번쨰는 입력층과 투사층 사이의 가중치 W는 V x M행렬이며, 투사층에서 ㅇ출력층 사이의 가중치 W'는 M x V행렬이라는 점입니다. 여기서 V는 단어 집합의 크기를 의미합니다. 위의 예시에서는 one-hot vector의 차원이 7이므로 M이 5라는 가정하에 W는 7 x 5행렬이 되겠습니다. W'는 5 x 7행렬이 자연스레 될것입니다.
이 두가지 행렬은 서로를 전치한 것이 아니라, 서로 다른 행렬이라는 점에 주의해야합니다. 그리고 신경망을 초기화할 때에는 랜덤값으로 가중치 행렬 W, W'를 초기화합니다. 즉 CBOW는 주변 단어를 중심으로 중심 단어를 더 정확히 맞추기 위해 계속해서 이 W, W'를 학습해가는 구조라고 보시면 됩니다.
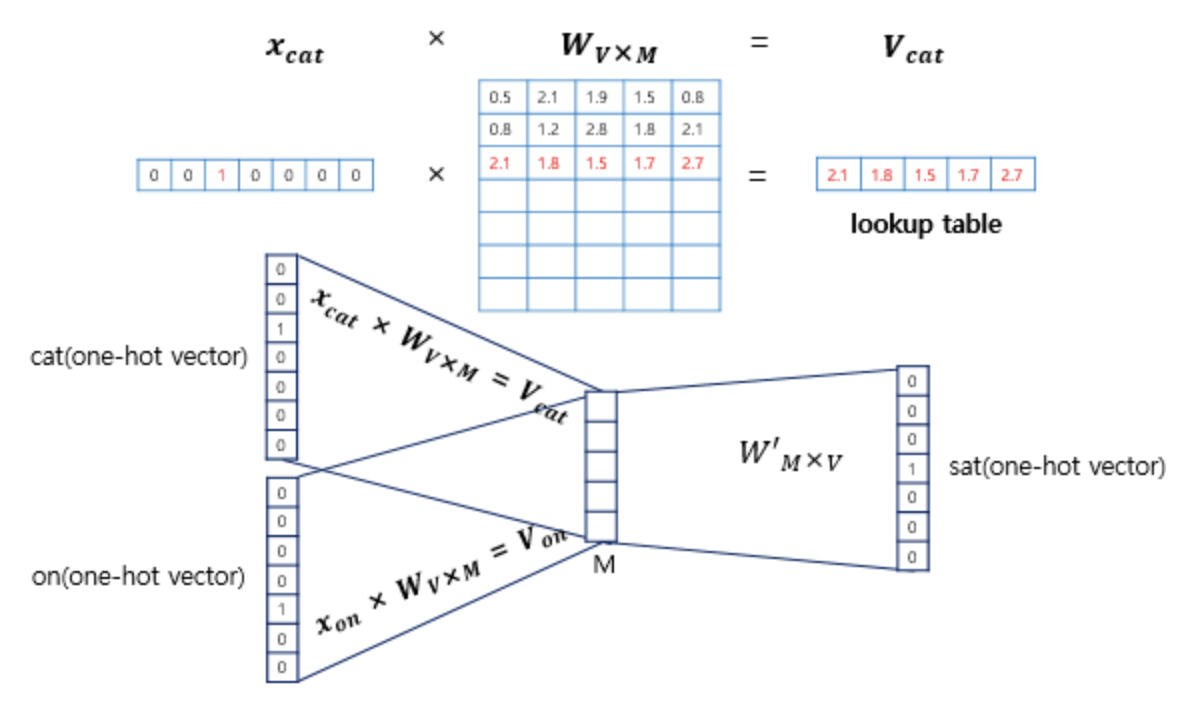
$x_{cat} x W_{V x M} = V_{cat}$이 됩니다. 즉 i번째 인덱스에 1이라는 값을 가지고 그 외의 0의 값을 가지는 입력 벡터와 가중치 W 행렬의 곱은 사실 W행렬의 i번째 행을 그대로 읽어오는 것과 동일하게 됩니다. 이 작업을 룩업 테이블(lookup table)이라고 합니다. 앞서 CBOW의 목적은 W, W'를 잘 훈련시키는 것이라고 언급한적이 있는데, 그 이유가 여기서 lookup해온 W의 각 행벡터가 Word2Vec 학습 후에는 각 단어의 M차원의 임베딩 벡터로 간주되기 때문입니다.
이렇게 주변 단어어의 one-hot vector에 대해서 가중치 W가 곱해서 생겨진 결과 벡터들은 투사층에서 만나 이 벡터들의 평균인 벡터를 만들게 됩니다. 나눌때에는 2xn(=windo_size)여야 한다는점 주의해야 합니다. 이 부분은 CBOW가 Skip-Gram과 다른 차이점이기도 합니다.
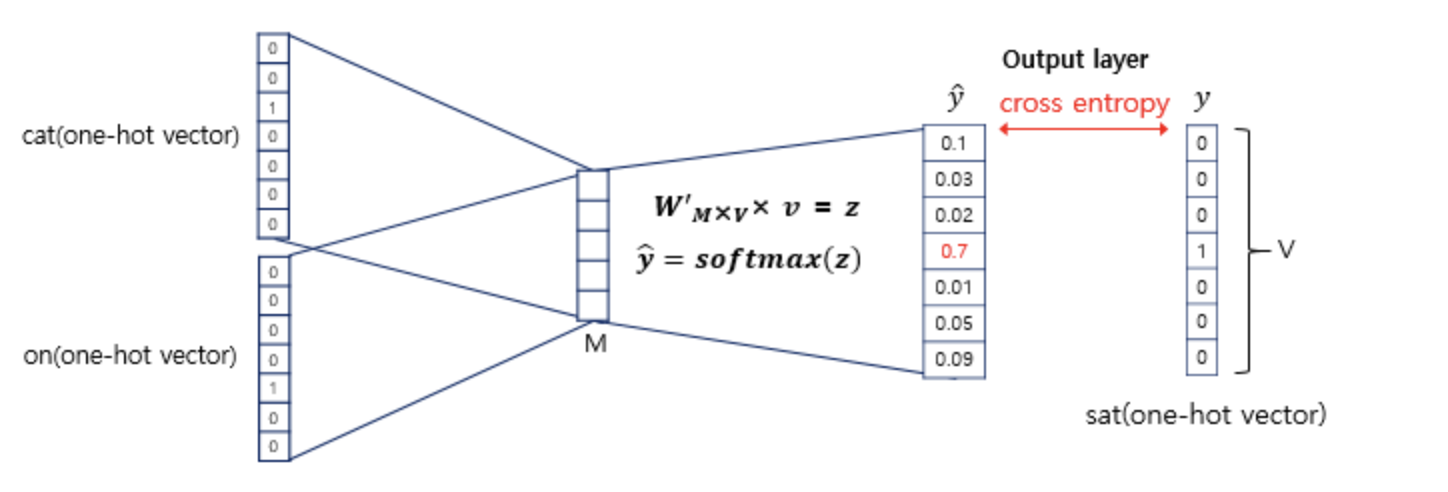
구한 평균 벡터는 두번째 가중치 행렬 W'과 곱해집니다. 이 벡터에 CBOW는 소프트맥스(softmax) 함수를 지나면서 벡터의 각 원소들의 값은 0과 1사이의 실수로, 총 합은 1이 되게 바뀝니다. Multi-class Classification을 위한 일종의 스코어 벡터(score vector)입니다. 그리고 $\hat{y}$를 예측한 스코어 벡터라고 하면, 중심 단어의 one-hot vector를 $y$라고 했을 때, 두 벡터값의 오차를 줄이기 위해 cross-entropy loss를 사용해서 Gradient Descent를 진행해 나갑니다.
Skip-gram
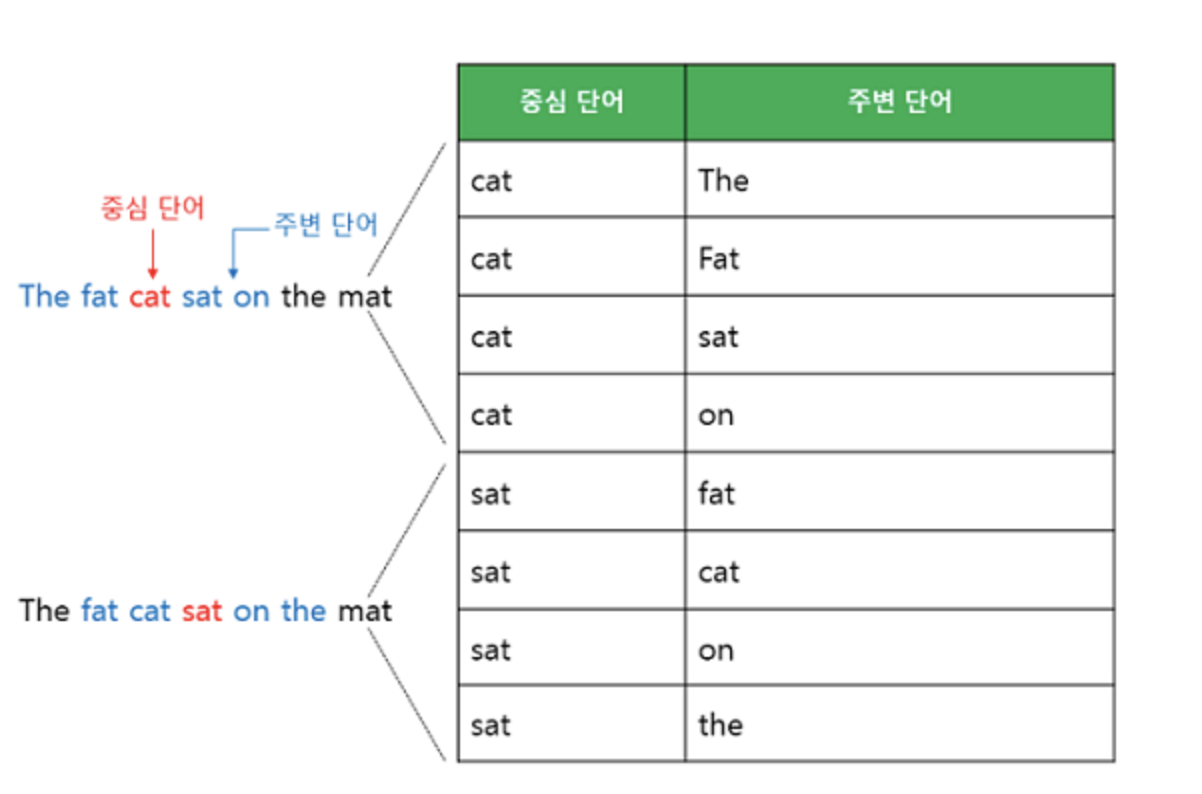
Skip-gram은 위에서도 말했지만 중심 단어에서 주변 단어를 예측합니다. 윈도우 크기 2일때, 데이터셋은 위와같이 구성됩니다.
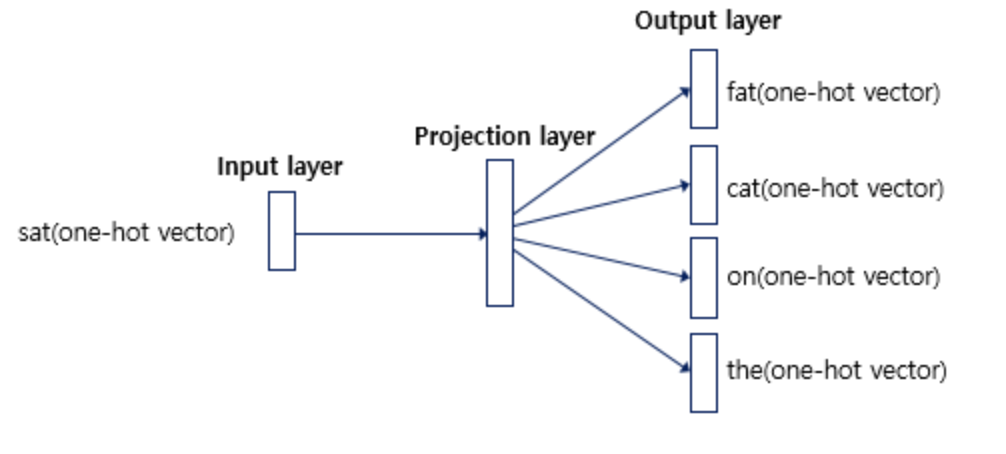
중심 단어에 대해서 주변 단어를 예측하므로 투사층에서 벡터들의 평균을 구하는 과정은 없습니다. 여러 논문에서 성능 비교를 진행해씅ㄹ 때 전반적으로 Skip-gram이 CBOW보다 성능이 좋다고 알려져 있다고 합니다.