해당 논문을 읽기 전에 제가 조사한 몇가지에 대해 정리해보도록 하겠습니다.
CNN에서 filter의 크기가 끼치는 영향
합성곱 신경망(Convolution Neural Networks, CNN)에서 필터의 크기는 네트워크가 이미지의 어떤 부분을 인식하는 데 얼마나 많은 정보를 사용하는지 결정합니다. 필터의 크기는 아래와 같은 영향을 끼칩니다.
- 수용 필드(Receptive Field): 필터의 크기는 각 출력 픽셀이 입력 이미지의 어떤 부분을 '보는' 범위, 즉 수용 필드를 결정합니다. 큰 필터(예: 5x5 또는7x7)는 더 넓은 수용 필드를 가지므로 이미지의 더 넓은 부분을 고려합니다. 이는 더 큰 패턴이나 객체를 인식하는 데 도움이 될 수 있습니다.
- 파라미터의 수: 필터의 크기가 클수록 학습해야 하는 파라미터의 수가 늘어납니다. 예를 들어, 5x5 필터는 25개의 가중치를 가지며, 3x3 필터는 9개의 가중치를 가집니다. 이는 모델의 복잡성과 계산 비용에 영향을 미칩니다.
- 공간적 해상도: 작은 필터(예: 1x1 또는 3x3)는 더 세밀한 공간 정보를 캡처할 수 있습니다. 이는 텍스처, 엣지, 작은 세부 사항 등의 더 세밀한 패턴을 인식하는 데 더 도움이 될 수 있습니다.
- 계층적 표현: 작은 필터를 사용하는 여러 개의 연속된 합성곱 계층은 큰 필터를 사용하는 단일 합성곱 계층과 동일한 수용 필드를 가질 수 있습니다. 이는 우리가 지금 알아볼 "Very Deep Convolutional Networks for Large-Scale Image Recognition" 논문에서 제안한 VGG 네트워크의 핵심 아이디어 입니다.
따라서 필터의 크기는 모델의 성능, 학습 속도, 그리고 인식 능력에 중요한 역할을 합니다. 이러한 요소를 고려하여 문제에 가장 적합한 필터 크기를 선택해야 합니다.
1x1 컨볼루션의 의미
1x1 컨볼루션은 합성곱 신경망에서 사용되는 특별한 유형의 컨볼루션입니다. 이는 필터의 크기가 1x1이라는 것을 의미합니다.
- 채널 수 조절: 1x1 컨볼루션은 입력 특징 맵의 채널 수를 조절하는 데 사용될 수 있습니다 예를 들어, 64개의 입력 채널이 있고 1x1 컨볼루션 레이어가 32개의 필터를 가지고 있다면, 출력 특징 맵은 32개의 채널을 가질 것입니다. 이는 모델의 복잡성을 줄이고 계산 효율성을 높이는 데 도움이 될 수 있습니다.
- 비선형성 추가: 1x1 컨볼루션 레이어는 비선형 활성화 함수(예: ReLU)와 함께 사용되어 네트워크에 추가적인 비선형성을 도입할 수 있습니다. 이는 모델이 더 복잡한 패턴을 학습하는 데 도움이 될 수 있습니다.
Very Deep Convolutional networks for large-scale image recognition

우선 우리가 늘 하던데로 초록을 보고 시작해 봅시다. 대충 읽어보면, 연구진은 large-scale 이미지들에서 network의 depth가 증가시킬 수 있음을 very small (3 x 3) convolution filter 를 통해 해결했고, 이전의 AlexaNet등과 비교했을 때 네트워크의 이미지 분류 정확도를 매우 높일 수 있었다고 합니다. 그래서 2014 ImageNet 대회에서 1등을 했다고도 하네요! 그리고 이 네트워크는 다양한 분야, 데이터 셋에서도 적용 가능하며 state-of-the-art result! 즉 환상적인 결과를 이루어냈다고 합니다.
초록도 읽었으니 논문의 내용을 보면서, 이 VGG 모델이 어떻게 이미지 분류 문제에서 이토록 좋은 성과에 도달할 수 있었는지를 확인해 보겠습니다. 참고로 VGG-16의 의미는 아래와 같습니다.
- VGG: Visual Geometry Group
- 16: 16 layers
따라서 신경망 모델의 깊이에 따라 VGG-19혹은 VGG-n(n > 19)가 될 수 있는 것이죠.
그럼 VGG-16 모델은 어떻게 16-19 레이어와 같이 깊은 신경망 모델의 학습을 성공했을까요? 그리고 왜 모든 Convolutional layer에서 3x3 필터만 사용했을까요?? 이 두 질문에 답할 수 있는 것이 VGG 논문의 핵심이자 모든 것이라고 할 수 있습니다.
VGG-16 네트워크의 구조

기존의 AlexNet(2012)의 8-layers 모델보다 위와같이 VGG16 Arch는 깊이가 2배 이상 깊은 네트워크의 학습에 성공했다고 합니다. 여기서 VGG 모델이 16-19 레이어에 달하는 깊은 신경망을 학습할 수 있었던 것은 모든 합성곱 레이어에서 3x3 필터를 사용했기 때문이라고 할 수 있습니다. 바로 VGG-16 Architecture의 구성에 대해 알아보겠습니다.
- 13 Convolution Layers + 3 Fully-connected Layers
- 3x3 convolution filters
- stride: 1 & padding: 1
- 2x2 max pooling (stride: 2)
- ReLU
즉 깊이에 따른 레이어의 크기를 보기 위해 논문에 있는 Table1 을 참조해 보겠습니다. 여기서 conv3은 3x3 필터를, conv1은 1x1 필터를 의미합니다. 또한 conv3-N에서 N은 필터의 개수에 해당합니다. 예를 들어 conv3-64는 64개의 3x3 필터를 학습 매개변수로 사용했다는 의미입니다.
본 논문에서 VGG의 컨볼루션 신경망이 다른 네트워크의 topology보다 덜 복잡해서 공간적 해상도가 덜 빠르게 감소한다고 되어있습니다. 여기서 컨볼루션 신경망에서 특징 맵 공간적 해상도 빠르게 감소한다는 것은 네트워크 레이어를 거치면서 이미지의 크기(즉, 너비와 높이) 가 점차적으로 줄어든다는 것을 말합니다. (* 여기서 이런 구절이 나타난 이유는 뭔가 뒤에서도 리뷰할 것이지만 해당 논문과 independently하게 개발되어진, GoogLeNet과 차별점을 말하고 싶었기 때문이 아닐까? 생각이 듭니다. 이는 VGG와는 다르게 1x1 conv, 5x5 conv를 사용합니다, 즉 작은 필터를 통해 deep network를 구성했다는 점에서는 동일한 셈이죠! )
이는 주로 폴링 레이어(pooling layer)또는 스트라이드(stride)가 큰 컨볼루션 레이어 때문에 발생합니다. 폴링 레이어는 주로 특징 맵의 공간적 해상도를 줄이는 데 사용되며, 이는 네트워크가 더 큰 수준에서 특징을 학습하도록 돕습니다. 이러한 공간적 해상도의 감소는 계산 효율성을 높이고, 과적합을 방지하는 데 도움이 됩니다. 또한, 공간적 해상도가 감소함에 따라, 각 특징이 입력 이미지의 더 넓은 영역을 커버하게 되므로, 네트워크는 더 고차원적인 특징을 학습할 수 있게 되는 것이지요.
VGG에서는 이러한 공간적 해상도가 급격하게 줄어들지 않습니다. 하지만 이도 아래 구조를 보면 알 수 있겠지만, (3x3 컨볼루션 -> maxpool) 을 하는 과정을 어쨌든 거칩니다. 따라서 VGG 네트워크는 작은 수용 필드를 사용하여 더 깊은 네트워크를 구성하면서도, 폴링 레이어를 통해 특징 맵의 공간적 해상도를 점진적으로 감소시킨다고 볼 수 있는 것이죠. 이는 네트워크가 더 고차원적인 특징을 학습하면서도 계산 효율성을 유지하도록 돕습니다!
근데 요즘의 네트워크는 "Dilated Convolutions" 또는 "Spatial Pyramid Pooling" 등은 다른 방법을 사용하여 이러한 이점을 얻기도 한다고 합니다.

신경망의 마지막 3 Fully-Connected Layers는 각각 4096, 4096, 1000개의 유닛으로 구성되어 있으며, 출력층(1000: class의 수)는 classification을 위한 softmax 함수를 사용합니다. 위의 표에서 구성 'D'에 대한 VGG-16을 예로 들어보겠습니다.

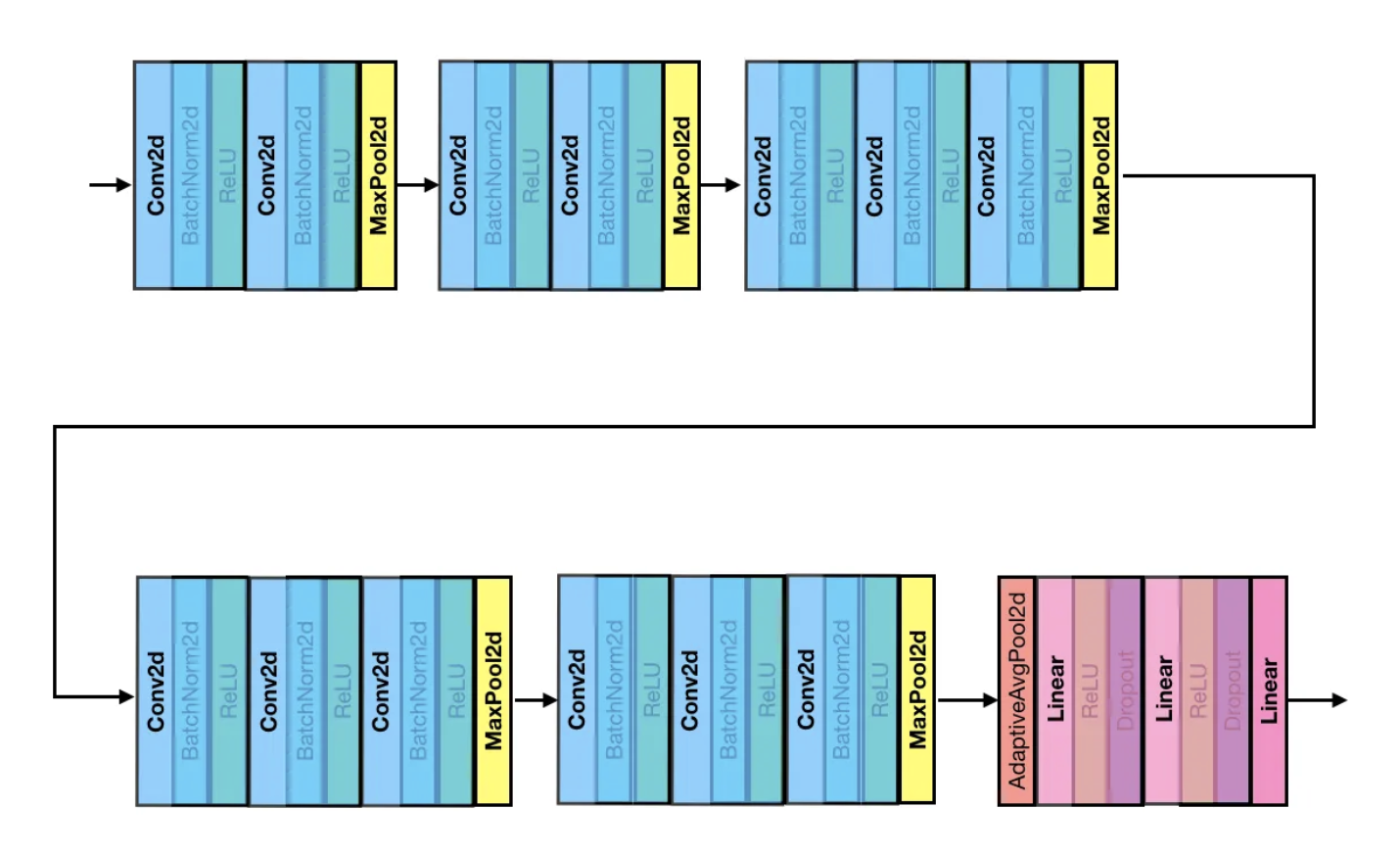
사실 위 그림에서 BN이 포함된 버전이 주로 사용된다고 합니다. 그걸 그려보면 아래와 같습니다.
VGG 모델 이전에 Convolutional Network를 활용하여 이미지 분류에서 좋은 성과를 보였던 모델들은 비교적 큰 Receptive Field를 갖는 11x11필터나 7x7필터를 포함합니다.
그러나 VGG 모델은 오직 3x3 크기의 작은 필터만 사용했음에도 이미지 분류 정확도를 비약적으로 개선시켰습니다. 이부분에서 본 논문이 우리에게 주는 통찰력이 주는 바가 큽니다.
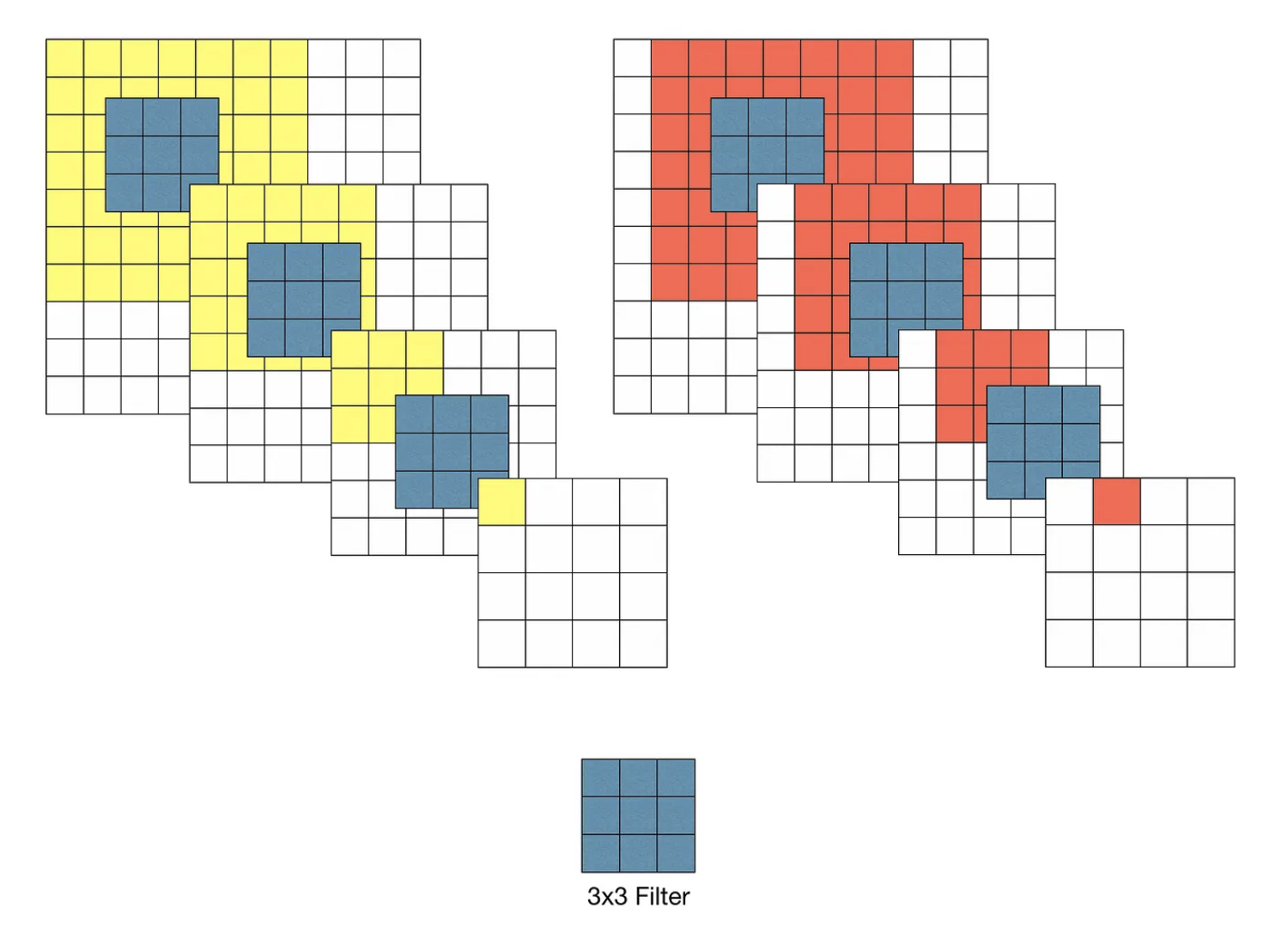
위와같이 3x3 필터를 이용할 경우 3-layer convolution을 반복했을 때 원본 이미지의 7x7 수용영역을 커버할 수 있게 됩니다. 즉 Stride가 1일 때, 3차례의 3x3 Conv 필터링을 반복한 특징맵은 한 픽셀이 원본 이미지의 7x7 Receptive field의 효과를 볼 수 있다는 것입니다. 그럼 커버할 수 있는건 알겠는데, 두 방법에 어떠한 차이가 있는지 알아보겠습니다.
1. 결정 함수의 비선형성 증가
각 Convolution 연산은 위 표에서도 볼 수 있다 싶이 Conv2d -> BN - ReLU 이 시퀀스를 거치는 것을 볼 수 있습니다. 이렇게 하는것이 성능상의 이점이 가장 크기 때문이기도 합니다. 여기서 각 Convolution 연산은 ReLU 함수를 포함하게 됩니다. 다시 말해, 1-layer 7x7 필터링의 경우 한 번의 비선형 함수가 적용되는 반면에 3-layer 3x3 필터링은 세 번의 비선형 함수가 적용됩니다.
2. 학습 파라미터 수의 감수
Convolutional Network 구조를 학습할 때, 학습 대상인 가중치(weight)는 필터의 크기에 해당됩니다. 따라서, 7x7 필터 1개에 대한 학습 파라미터 수는 49개이고 3x3 필터 3개에 대한 학습 파라미터 수는 27개가 되는 것입니다.
물론 위와 같은 특징이 모든 경우에 좋은 방향으로 작용하는 것은 아닙니다. 다시 말해, 무작정 네트워크의 깊이를 깊게 만드는 것이 장점만은 있는 것이 아닙니다. 여러 레이어를 거쳐 만들어진 특징 맵은 동일한 Receptive Field에 대해 더 추상적인 정보를 담게 됩니다. 목적에 따라서는 더 선명한 특징 맵이 필요하게 될 수도 있습니다.
모델의 학습

이제 VGG-16 원문에서 적용된 최적화 알고리즘에 대해 간단히 알아보겠습니다.
- Optimizing multinomial logistic regression (softmax)
- mini-batch gradient descent
- Momentum(0.9)
- 이 또한 GD(Gradient Descent)의 최적화를 위한 모멘텀값임
- Weight Decay(L2 Norm)
- 과적합을 방지하고 모델의 일반화 성능을 높임
- 논문에서 소개한 $L_{2}$ penalty multipler($\alpha$)는 $5*10^{-4}$
- Dropout(0.5)
- 과적합 방지를 위한 dropout 값
- 논문에서는 이가 first two fully-connected layers에만 적용했다고 되어 있음
- Learning rate 0.01로 초기화 하고 서서히 줄임
- 초기에는 $10^{-2}$로 초기화 하고 decreased factor는 10으로 설정하고 validation set에서는 이를 적용해주지 않았다고 합니다.
- 이는 총 VGG net에서 3번 이루어 졌다고 하네요 -> 370K iteration (74epochs)
- 이는 다른 네트워크 보다 깊이가 깊고, 네트워크의 파라미터가 훨씬 많았지만, 수렴하는데 더 적은 epochs가 필요했다고 하네요!
- 이 이유는 논문에서 (a) implicit regularisation imposed by greater depth and smaller conv. 즉 더 깊은 레이어와 작언 크기의 conv 레이어에 강한 규제를 둔 이유고 (b) pre-initialisation of certain layers. 즉 몇 개의 레이어에 대해 미리 설정된 가중치 값으로 설정했기 때문이라고 합니다. -> 초기화 하는 방법은 뒤에서 좀 더 다루어 보도록 하겠습니다.
- 이는 다른 네트워크 보다 깊이가 깊고, 네트워크의 파라미터가 훨씬 많았지만, 수렴하는데 더 적은 epochs가 필요했다고 하네요!
보다보니까 Batch Normalization, ResNet에서 적용한 것들과 비슷하다는 느낌을 받을 수 있었습니다. 이러한 학습 알고리즘은 본 논문의 핵심과는 벗어나며, 모델과 무관하게 얼마든지 변경될 수 있는 부분이므로 자세히는 다루지 않겠습니다.
가중치 초기화 ( pre-initialisation)
딥러닝에서 신경망 가중치의 초기화는 학습 속도 및 안정성에 큰 영향을 줄 수 있기 때문에 어떤 방식으로 초기화할 것인지는 중요한 문제중에 하나입니다. VGG 연구팀은 이러한 문제를 보완하고자 다음과 같은 전략을 세우게 되었습니다.
- 상대적으로 얕은 11-layer 네트워크를 우선적으로 학습합니다. 이때, 가중치는 정규분포를 따르도록 임의의 값으로 초기화합니다.
- 어느 정도 학습이 완료되면 입력층 부분의 4개의 층과 마지막 3개의 fully-connected layer의 weight를 학습할 네트워크의 초깃값으로 사용합니다.
깊은 신경망에서는 가중치 초기화가 잘못되면 학습이 정체될 수 있습니다. (조사해보면 알겠지만, 분산이 크면 vanishing gradient 문제가 발생할 수 있고, 작다면 모델의 표현력이 제한될 수 있다는 문제가 있습니다!) 그래서 VGG 네트워크는 먼저 얕은 네트워크를 무작위로 초기화시킨 다음에 학습시키고, 더 깊은 구조를 학습할 때 첫 번쨰 네 개의 컨볼루션 레이어와 마지막 세 개의 완전 연결 레이어를 네트워크 A의 레이어로 초기화 하는 것이죠. 즉 이러한 방법을 "사전 학습(pretraining)" 이라고도 부릅니다!
하지만 해당 논문을 제출 후 Glorot&Bengio (2010)이 무작위 초기화 절차를 이용하여 사전 훈련 없이 가중치를 초기화하는 것이 가능하다는 것을 알아냈는데, 이것이 Xavier와 LeCun 가중치 초기화 방법인데, 이것을 적용하면 레이어가 싶어진다고 하더라도 입력 분포가 바뀌지 않고 분산을 유지한체 종 모양을 유지할 수 있게 됩니다.
학습 이미지 크기 ( data agumentation )

모델 학습(Training) 시 입력 이미지의 크기는 모두 224x224 (S 값)로 고정하였습니다. 학습 이미지는 각 이미지에 대해 256x256 ~ 512x512 내에서 임의의 크기로 변환하고 크기가 변환된 이미지에서 개체(Object)의 일부가 포함된 224x224 이미지를 Crop하여 사용을 하였습니다.
1. 고정 스케일 훈련 (Fixed Scale Training)

여기서 istropically-rescaled 이란 용어는 이미지의 모든 차원이 동일한 비율로 조정된다는 것을 의미합니다. 이는 신경망이 다양한 크기의 이미지에 대해 일반화하는 능력을 향상시키는 데 도움이 될 수 있습니다. VGG 네트워크에서는 훈련 이미지를 SxS 크기로 isotropically rescale합니다. 여기서 S는 네트워크 마다 다르며, VGG네트워크에서는 위에서 언급했던 대로 224, 256, 384, 512등으로 설정됩니다. 이렇게 하면 네트워크는 다양한 크기의 이미지에 대해 효과적으로 학습할 수 있게 됩니다.
즉 정리하면 훈련 스케일 S(훈련 이미지의 가장 작은 측면을 등방성으로 재조정한 후 ConvNet에 입력으로 제공되는 크기)를 고정합니다. 이 경우, S는 224이상의 어떠한 값도 될 수 있으며, S=224일 경우 ConvNet 입력은 훈련 이미지의 전체 통계를 캡처하고, S가 224보다 훨씬 큰 경우, 입력은 이미지의 작은 부분에 해당하게 됩니다. 이들은 실험에서 두 가지 고정 스케일인 S=256과 S=384에서 모델을 평가했습니다. 특정 ConvNet 구성에 대해, 먼저 S=256을 사용하여 네트워크를 훈련시키고, S=384네트워크의 훈련 속도를 높이기 위해 이를 S=256으로 사전 훈련된 가중치로 초기화하고, 더 작은 학습 초기 학습률인 $10^{-3}$ 를 사용했다고 합니다.
2. 다중 스케일 훈련 (Multi-Scale Training)



이처럼 학습 데이터를 다양한 크기로 변환하고 그 중 일부를 샘플링해 사용함으로써 아래와 같은 효과를 얻을 수 있었다고 합니다.
정리하자면 이 접근 방식에서는 각 훈련 이미지가 특정 범위 [Smin, Smax]에서 S를 무작위로 샘플링하여 개별적으로 재조정됩니다. 이미지 내의 객체들이 다른 크기를 가질 수 있기 때문에, 이를 훈련 과정에서 고려하는 것이 유익합니다. 이는 또한 스케일 지터(다양한 크기에 대해 모델을 더 robust하게 만드는 데이터 증강기법) 를 통한 훈련 세트 증강으로 볼 수 있으며, 단일 모델이 다양한 스케일에서 객체를 인식하도록 훈련되는 것입니다. 속도 문제로 인해, 같은 구성을 가진 단일 스케일 모델의 모든 계층을 사전에 훈련된 고정 S=384를 사용하여 미세 조정함으로써 다중 스케일 모델을 훈련시켰습니다.
- 한정적인 데이터의 수를 늘릴 수 있다. -> 이를 Data augmentation이라고 했죠
- 하나의 오브젝트에 대한 다양한 측면을 학습 시 반영시킬 수 있다. 변환된 이미지가 작을수록 개체의 전체적인 측면을 학습할 수 있고, 변환된 이미지가 클수록 개체의 특정한 부분을 학습에 반영시킬 수 있게 됩니다.
- 위의 사슴 이미지만 봐도 딱 직관적으로 알 수 있습니다.
두 가지 모두 Overfitting 을 방지하는 데 도움이 됩니다.
실제로 VGG 연구팀의 실험 결과에 따르면 다양한 스케일로 변환한 이미지에서 샘플링하여 학습 데이터로 사용한 경우가 단일 스케일 이미지에서 샘플링 한 경우보다 분류 정확도가 좋았다고 합니다.
Train
제가 이해한 바를 그대로 요약해 보겠습니다.
1) 원본 이미지를 먼저 istropically(즉, 가로와 세로 비율을 유지하면서) S크기로 리사이징합니다. 이 때 S값은 iteration마다 랜덤하게 결정될 수 있습니다. 그러나 모든 S값은 224보다 크거나 같아야 합니다.
2) 이렇게 리사이징된 이미지에서, 224x224 크기의 patch를 랜덤하게 추출(crop)합니다. 이런 방식으로 데이터의 다양성을 높일 수 있습니다.
3) 이렇게 추출한 224x224 크기의 이미지 patch를 모델의 입력으로 사용해 학습을 진행시킵니다.
그리고 우리는 모델의 학습 가속을 위해 S=384로 설정된 파라미터들을 초기 가중치 값으로 설정해서, 이 파라미터 값에서 fine tuning을 해서 모델의 학습을 진행시켜 나가 모델의 학습 진행을 촉진시킬 수 있다! 라는 것입니다.
Fully-convolutional Nets

Training 완료된 모델을 테스팅할 때는 신경망의 마지막 3 Fully-Connected layers를 Convolutional layers로 변환하여 사용하였습니다.
첫 번째 Fully-Connected layer는 7x7 Conv로, 마지막 두 Fully-Connected layer는 1x1 Conv로 변환하였습니다. 이런식으로 변환된 신경망을 Fully-Convolutional Networks라 부릅니다.
Fully-COnvolutional Networks는 모든 레이어가 컨볼루션 레이어로 구성된 신경망을 의미합니다. 이는 전통적인 컨볼루션 신경망(CNN)에서 일반적으로 사용되는 완전 연결 레이어(fully connected layers)또는 밀집 레이어(dense layers)를 사용하지 않는다는 것을 의미합니다.
일반적인 CNN구조에서는, 여러개의 컨볼루션 레이어와 폴링 레이어를 거친 후에, 마지막에 하나 이상의 완전 연결 레이어가 있습니다. 이 완전 연결 레이어는 일반적으로 분류 작업을 수행하며, 모든 입력 픽셀이 독립적으로 처리되므로 공간적 정보가 손실될 수 있습니다.
근데 FCN에서는 이러한 완전 연결 레이어 대신에 컨볼루션 레이어를 사용합니다. 이렇게 하면 네트워크는 공간적 정보를 유지하면서 복잡한 특징을 학습할 수 있게 됩니다. 또한, 이러한 네트워크는 임의의 크기의 입력을 처리할 수 있으므로, 이미지 분할과 같은 픽셀 수준의 예측 작업에 특히 유용합니다.
그렇다면 저는 또 의문이 들었습니다. 그럼 1x1 conv와 flattening의 차이점은 무엇일까요? 그걸 아래에 정리했습니다.
- 1x1 conv: 이는 컨볼루션 레이어에 사용되는 연산입니다. 이는 피처 맵의 깊이(채널 수)를 변환하는 데 사용됩니다. 이는 또한 네트워크의 복잡성을 줄이고, 계산 효율성을 향상시키며, 동시에 네트워크의 표현력을 유지하는 데 유용하게 됩니다. 이는 그래도 각 피처 맵의 각 픽셀에 대해 별도의 학습 가능한 가중치를 가지므로, 네트워크는 각 채널의 정보를 독립적으로 학습하고 변환할 수 있습니다.
- Flattening: 이는 신경망에서 피처 맵을 1차원 벡터로 변환하는 연산입니다. 이는 주로 2차원 또는 3차원의 피처 맵을 1차원의 벡터로 변환하여 완전 연결 레이어에 공급할 수 있게 합니다. 이는 공간적 정보를 손실할 수 있으며, 모든 피처가 독립적으로 처리하는 완전 연결 레이어에 적합한 형태로 데이터를 변환합니다.
즉 두개가 사용되는 컨텍스트가 매우 다르다는 것을 의미합니다. 이와 관련된 논문은 추후에 첨부할 예정입니다. 관련 논문은
Fully Convolutional Networks for Semantic Segmentation (CVPR 2015) 입니다. 바로 다음에 리뷰할 논문은 Going Deeper With Convolutions (CGPR 2016) GoogLeNet과 관련된 논문입니다!
test 과정을 정리해보면 아래와 같을 것입니다.
- 주어진 입력 이미지는 먼저 사전에 정의된 가장 작은 이미지 변으로 등방향 리스케일링(istropically rescaled)됩니다. 이 리스케일링의 크기는 Q라고 표시하며, 테스트 스케일로도 불릅니다. 이 Q는 train scale size (S) 와 반드시 동일하지 않아야 합니다.
- 리스케일된 테스트 이미지 위에 네트워크가 밀도 높게 (densly) 적용됩니다. 이 과정에서 완전 연결 계층 (fully connected layers)는 먼저 컨볼루션 계층으로 변환됩니다. 위에서 말한 7x7 Conv -> 1x1 Conv -> 1x1 fully connected (1000 class)
- 결과적으로 완전 컨볼루션 네트워크가 전체(not cropped) 이미지에 적용됩니다. 결과는 클래스 수에 같은 수의 채널을 갖는 클래스 점수 맵이며, 공간 해상도는 입력 이미지 크기에 따라 다릅니다.
- 이미지의 클래스 점수를 고정 크기 벡터로 얻기 위해, 클래스 점수 맵은 공간적으로 평균됩니다 (합계 폴링)
- 데이터 셋은 이미지를 horizontal하게 뒤집는 것으로 확장됩니다. 원래 이미지와 뒤집힌 이미지의 소프트맥스 클래스 사후 확률은 최종 점수를 얻기 위해 평균됩니다.
test image에도 crop을 적용해 보았지만, 이는 더 나은 성능을 보였지만 연산량의 관점에서 매우 비효율적이라고 논문에서 나와있습니다! 근데 사실 저도 image segmentation과 관련된 논문을 읽어보지 않았기 때문에, 관련 논문을 추후에 읽어보고 해당 내용을 다시 보충해 보도록 하겠습니다.
Classification experiments
우선 dataset으로는 1000개의 클래스에 대한 이미지들이 포함되어 있고, 이것은 3가지 셋(training: 1.3M, validation: 50K, testing: 1000K) 으로 나누었습니다. 평가기준은 top-1, top-5 error를 이용하였으며 전자는 예측이 잘못된 이미지의 비율, 후자는 top-5 예측된 범주에 정답이 없는 이미지의 비율입니다.
여기서 top-5 error는 이미지 분류 작업에서 자주 사용되는 평가 지표 중 하나로서, 모델이 예측한 확률이 가장 높은 상위 5개의 클래스 중에 실제 정답 클래스가 없을 때 발생하는 오류를 의미합니다. 이는 특히 클래스 수가 많은 상황에서는 중요한 평가 지표가 될 수 있습니다!
Single Scale evaluation
이는 test set의 size가 고정된 단일 규모 평가입니다.

- AlexNet에서 이용되었던 LRN(local response normalisation)이 효과가 없었습니다.
- 깊이가 깊어질 수록 Error가 감소한다는 것을 볼 수 있습니다.
- C가 D보다 성능이 낮고 B보다 성능이 높습니다. 이는 추가적인 비선형성은 도움이 되는 반면에 conv filter를 사용하여 공간적인 맥락을 포착하는 것이 중요하다는 것을 나타냅니다. 그리고 5x5 filter를 이용하는 것보다 3x3 filter를 2개 이용하는 것이 성능 향상에 도움이 된다고 합니다. -> 이는 계산 복잡도 측면에서도 더 효율적이라고 논문에서 수식으로 보여줍니다.
- 다양한 scale[256;512]로 resize한 것이 고정된 scale의 training image보다 성능이 좋았습니다.
- 제가 이전에도 다양한 scale의 training set augmentation은 이미지의 통계값을 다양한 척도로 포착하는 데에 도움이 되어서 오버피팅을 방지하고 모델의 성능이 더 높아질 수 있다고 말했었습니다.
여기서 제가 누누히 말했지만 test 할떄에는 FCN(Fully Convolutional Network) 으로 동작해서 test Q가 마음대로 설정될 수 있는 것입니다. FCN은 입력 데이터의 크기에 영향을 받지 않는다는 특징이 있습니다. 그리고 네트워크의 출력을 공간적 차원에 대해 평균내어 전체 이미지에 대한 단일 클래스 점수 벡터를 생성한 다음에, 가장 높은 점수를 가진 클래스 예측값으로 씁니다.
Multi-scale evaluation
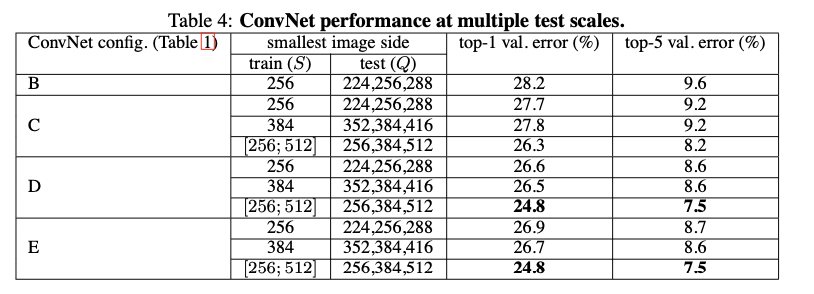
이제 test set의 다양한 scale에 대한 실험입니다. 실험 결과 test 이미지를 다양한 scale로 resize했을 때, 단일 size보다 더 나은 성능을 보였습니다.
모델이 훈련하는 동안, 우리는 데이터 증강(data augmentation)을 사용하여 이러한 변화에 대응하려고 했습니다. 이는 이미지를 회전하거나 뒤집는 등의 방법을 포함할 수 있다고 했었습니다. 마찬가지로, 우리는 스케일 지터(scale jittering)를 사용하여 모델이 다양한 객체 크기에 대응하도록 훈련할 수 있었습니다. 테스트 시에 이미지의 스케일을 바꾸는 것은 이와 비슷한 원리로 작동합니다. 모델이 이미지를 보는 "시각"을 바꾸어, 서로 다른 스케일에서 보이는 특징들을 감지하도록 합니다. 이렇게 하면, 모델이 작은 객체를 놓치지 않을 뿐만 아니라, 큰 객체의 전체적인 모양을 더 잘 이해할 수 있게 됩니다. 그 결과, 전반적인 예측 성능이 향상되고 테스트 에러율이 감소하게 되는 것이죠. -> 이 과정에서
위의 Signel scale evaluation과 비교했을 때 D의 [256;512]의 top-1 val error율이 25.6 -> 24.8로 낮아진 것을 볼 수 있습니다.
스케일 지터(scale jittering)
이는 컴퓨터 비전과 머신러닝에서 일반적으로 사용되는 기술로, 학습 데이터의 다양성을 증가시키는 한 가지 방법입니다. 이는 이미지 분류와 같은 작업에서 모델의 일반화 능력을 향상시키는 데에 도움이 됩니다. 이는 일반적으로 훈련 과정 중에 적용되며, 각 에폭에서 이미지의 크기를 무작위로 조정합니다. -> 일반적으로 이미지가 신경망에 투입되기 전에 고정된 크기로 다시 조정(rescale)됩니다. 즉 스케일 지터 적용 -> 모든 이미지가 224x224픽셀로 다시 조정
참고로 이미지를 리스케일하려면 보간(Interpolation) 기법을 사용해야 합니다~ 이도 나중에 Image segmentation할 떄 알아보겠습니다!
Multi-crop evaluation
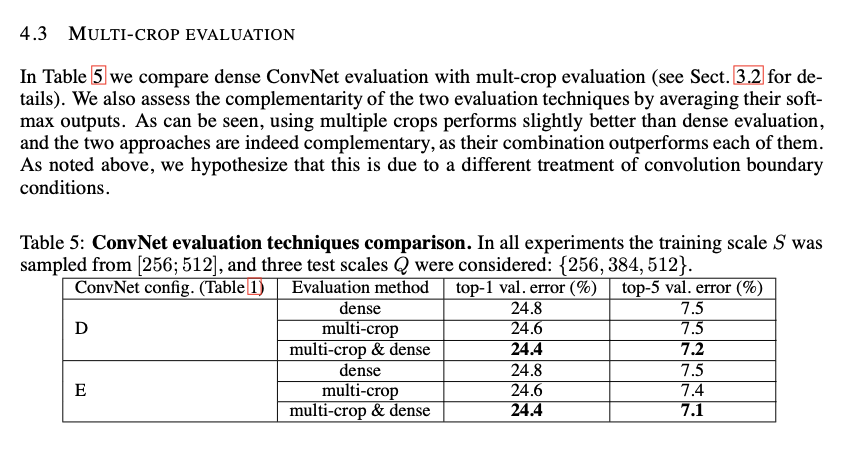
그리고 위와 비슷하게 Test 이미지를 다양하게 crop을 해주어 더 나은 성능을 얻었다고 합니다. 여기서 multi-crop 이 dense보다 더 좋은 성능을 나타낸 것을 볼 수 있습니다. 여기서 S는 [256;512], Q는 {256, 384, 512} 가 고려되었다고 합니다. 그리고 두개를 softmax 떄려서 평균 낸 것이 성능이 가장 좋은 것을 볼 수 있습니다.
ConvNet fusion
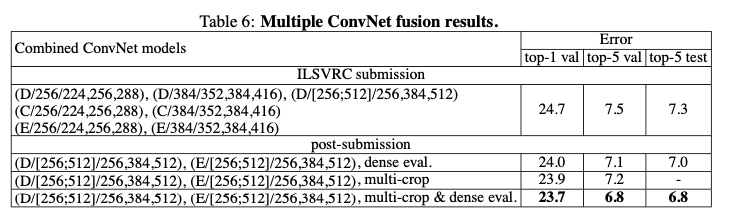
그리고 앙상블에 대한 내용입니다. 모델 7개를 앙상블한 ILSVRC 제출물은 test set top-5 error가 7.5% 가 나왔고, 추후에 모델 2개를 앙상블 하여 test set top-5 error를 6.8% 까지 낮추었다고 합니다.
'AIML > 딥러닝 최신 트렌드 알고리즘' 카테고리의 다른 글
| [ 딥러닝 - 모델구현 ] - VGG11/16/19 Net (0) | 2023.07.09 |
|---|---|
| [딥러닝 - 논문 리뷰 PRMI Lab] - Going Deeper with Convolutions (CVPR 2015) - GoogLeNet (0) | 2023.07.08 |
| [딥러닝 - PyTorch] - TORCH.NN 이 무엇일까? (0) | 2023.07.03 |
| [딥러닝 기초] - ResNET을 이해하기 위한 CNN 개요 (0) | 2023.06.30 |
| [딥러닝 논문 리뷰 - PRMI Lab] - Deep Residual Learning for Image Recognition (CVPR 2016) + 실습 (0) | 2023.06.29 |
![[ 딥러닝 논문리뷰 - PRMI Lab ] Very Deep Convolutional networks for large-scale image recognition (16-19 VGG net)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbSVxuA%2FbtsmHHD4Peu%2FDcRZ1aY5hGlYfZuKnkn8Ek%2Fimg.png)