https://www.acmicpc.net/problem/16975
16975번: 수열과 쿼리 21
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. 1 i j k: Ai, Ai+1, ..., Aj에 k를 더한다. 2 x: Ax 를 출력한다.
www.acmicpc.net
이전에 공부한 느리게 전파되는 세그먼트 트리와 관련된 문제입니다.

사실 이 문제는 lazy propagation을 사용하지 않고도 해결할 수 있다. 바로 펜윅트리인데요
펜윅트리란..?
https://www.acmicpc.net/blog/view/21
펜윅 트리 (바이너리 인덱스 트리)
블로그: 세그먼트 트리 (Segment Tree) 에서 풀어본 문제를 Fenwick Tree를 이용해서 풀어보겠습니다. Fenwick Tree는 Binary Indexed Tree라고도 하며, 줄여서 BIT라고 합니다. Fenwick Tree를 구현하려면, 어떤 수 X
www.acmicpc.net
이 글을 참조하여 간단히 BIT라고 불리우는 Fenwick Tree에 대해 설명해보겠습니다. Fenwick Tree를 구하려면, 어떤 수 X를 이진수로 나타냈을때, 마지막 1의 위치를 알면 됩니다. 마지막 1이 나타내는 값을 L[i]라고 했을 때, L[3] = 1, L[10] = 2이런 식이죠

수 N개를 이라고 했을 때, Tree[i]는 로부터 앞으로 개의 합이 저장되어 있습니다. 위 그림은 각각의 i에 대해서, 를 나타낸 표입니다. 아래 초록 네모는 i부터 앞으로 개가 나타내는 구간입니다.

그리고 위는 L[i]를 구하는 공식입니다. 원리는 위를 보면 쉽게 알 수 있습니다.
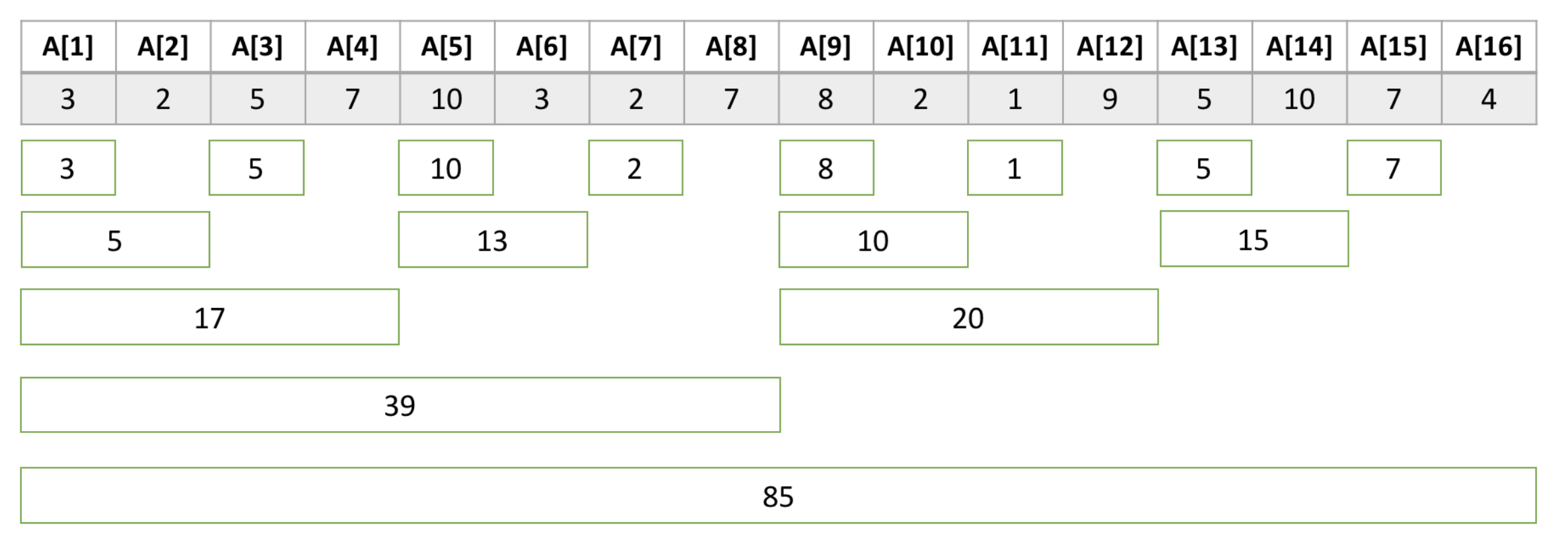
예를 들어 위 그림에서 Tree[12]에는 12부터 앞으로 개의 합은 가 저장되어 있는 것이라고 할 수 있습니다. 그리고 만약 이 펜윅 트리를 이용해서 은 를 통해 구할 수 있습니다. 아래와 같이 말이죠
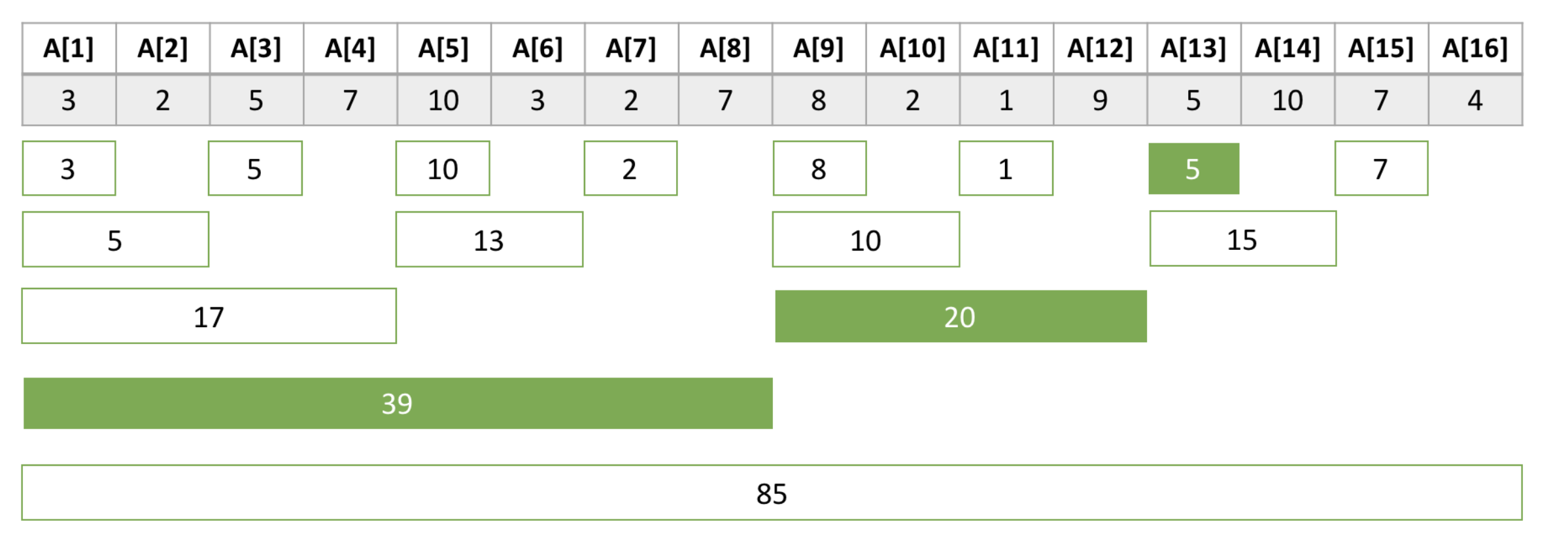
이를 코드로 나타내면 아래와 같습니다.
int sum(int i) { int ans = 0; while (i > 0) { ans += tree[i]; i -= (i & -i); } return ans; }
생각보다 간단하지,,, 않나요?? 그리고 구간합도 는 에서 를 뺀 값과 같은걸 알고 있습니다. 이를 통해 쉽게 구할 수 있습니다!!
변경도 간단히 코드로 나타내면, 어떤 수를 변경한 경우에는, 그 수를 담당하고 있는 구간을 모두 업데이트해주어야 합니다.
void update(int i, int num) { while (i <= n) { tree[i] += num; i += (i & -i); } }
ㅋㅋㅋ 서론이 길었습니다. 이처럼 펜윅 트리는 세그먼트 트리와는 다르게 부분합(첫 원소에서 부터 i개의 값)을 계산하는데 특화되었습니다. 백준님이 설명한 펜윅트리에서는 점 업데이트(Point Update)와 구간 쿼리(Range query)가 가능했습니다. 이를 그냥 세그먼트 트리를 이용하면 구간 업데이트마다 의 시간복도가 소요되므로 TLE가 발생합니다.
위 문제에서 질의하는 것은 아래 2가지 입니다.
- Query1: 에 k를 더한다.
- Query2: 를 출력한다.
그리고 길이가 N인 수열 A를 B로 표현하는데 . 이때 1번 쿼리의 경우 , . . . 가 됩니다. 즉 에는 +k, 에는 -k만 해주면 구간 업데이트를 구간의 끝점에만 적용하는 문제로 바꿀 수 있다는 것이죠
그럼 2번의 쿼리는 어떨까요. A[x]의 값은 B[1] + B[2] + ... + B[x]입니다. 즉 A를 B로 나타낸 펜윅 트리에서는 A원소의 값을 얻기 위해서 B의 1에서 x까지 구간의 합을 더해주기만 하면 된다는 것이죠.
하지만!! 저는 이런걸 떠올릴 실력이 아직 되지 못합니다.. 그래서 그냥 정석 풀이대로 한 점에서의 세그먼트 트리와 lazy propagation을 사용해서 아래와 같이 풀었습니다. 이에 대한 시간복잡도는 구간 업데이트, 범위 쿼리에 대해 으로 해결됩니다. 당연히 lazy propagation의 구현 방법마다 다 다르겠고, 예외 상황도 존재하지만요! 일반적인 상황에서를 말한겁니다!
import sys from math import ceil, log2 input = sys.stdin.readline def init(arr, tree, start, end, node): if start == end: tree[node] = arr[start] else: mid = (start + end) // 2 init(arr, tree, start, mid, node * 2) init(arr, tree, mid + 1, end, node * 2 + 1) def update_range(tree, lazy, start, end, node, idx_start, idx_end, add): if end < idx_start or start > idx_end: return if start >= idx_start and end <= idx_end: ''' 범위 내에 포함되는 경우는 lazy를 자식노드에 저장해주어야 한다. ''' tree[node] += add if start != end: lazy[node * 2] += add lazy[node * 2 + 1] += add return mid = (start + end) // 2 update_range(tree, lazy, start, mid, node * 2, idx_start, idx_end, add) update_range(tree, lazy, mid + 1, end, node * 2 + 1, idx_start, idx_end, add) def query(tree, lazy, start, end, node, target): ''' lazy를 처리하는 로직이 있어야 한다. -> lazy propagation하게 ''' if lazy[node] != 0: tree[node] += lazy[node] if start != end: lazy[node * 2] += lazy[node] lazy[node * 2 + 1] += lazy[node] lazy[node] = 0 if target < start or target > end: return 0 if start == target and end == target: return tree[node] mid = (start + end) // 2 return query(tree, lazy, start, mid, node * 2, target) \ + query(tree, lazy, mid + 1, end, node * 2 + 1, target) n = int(input()) arr = list(map(int, input().split())) h = ceil(log2(n)) tree_size = 1 << (h + 1) m = int(input()) # 세그먼트 트리와 lazy를 초기화한다. tree = [0] * 400001 lazy = [0] * 400001 # 세그먼트 트리 값 초기화 init(arr, tree, 0, n - 1, 1) for _ in range(m): what, *q = map(int, input().split()) if what == 1: left, right, add = q update_range(tree, lazy, 0, n - 1, 1, left - 1, right - 1, add) elif what == 2: target = q[0] print(query(tree, lazy, 0, n - 1, 1, target - 1))
https://www.acmicpc.net/problem/16978
16978번: 수열과 쿼리 22
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. 1 i v: Ai = v로 변경한다. 2 k i j: k번째 1번 쿼리까지 적용되었을 때, Ai, Ai+1, ..., Aj의 합을 출력한다.
www.acmicpc.net
그 다음은 수열과 쿼리 22입니다. 이는 세그먼트 트리에서 오프라인 쿼리를 연습하기 좋은 문제였습니다.
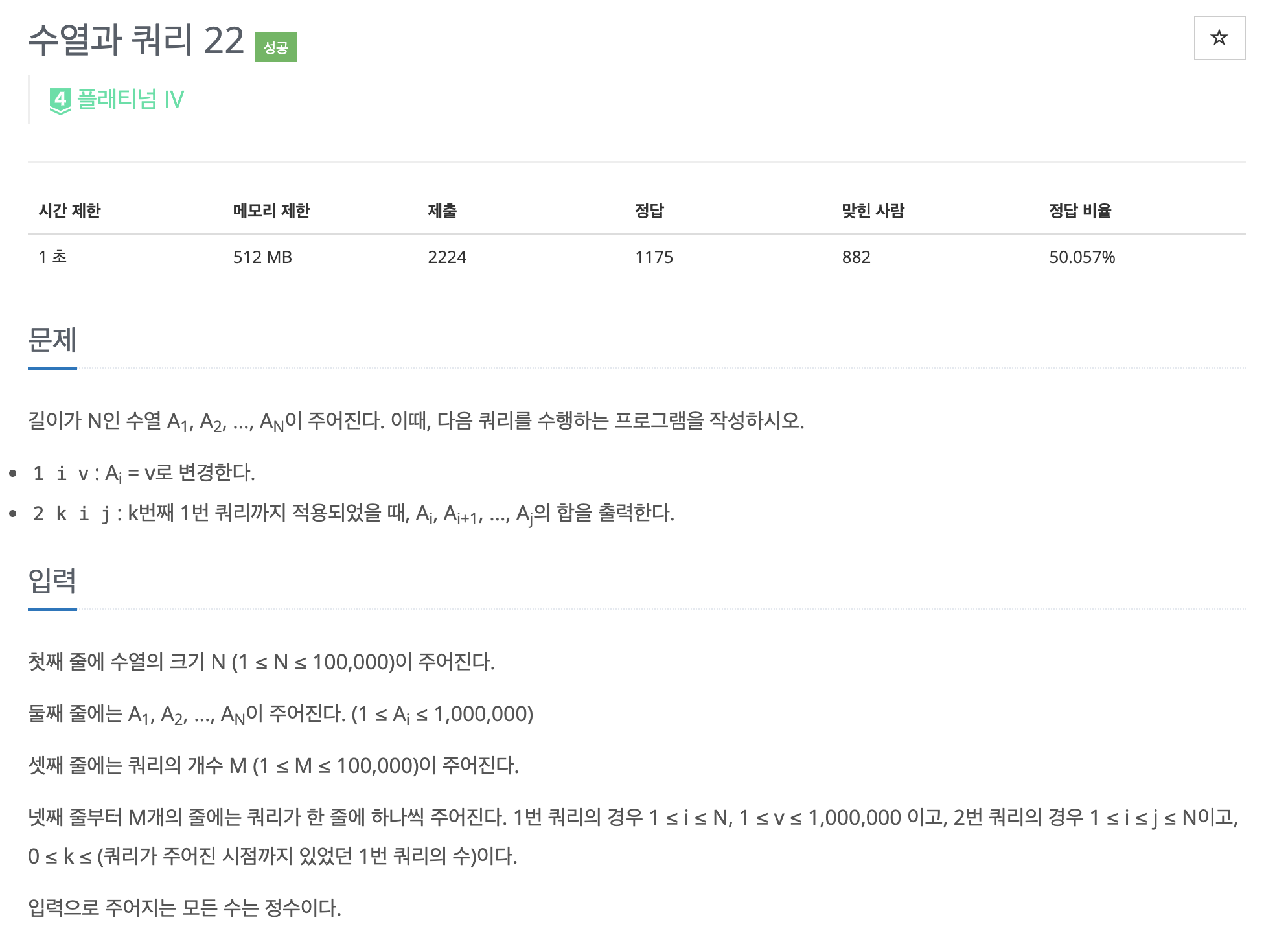
이 문제가 딱봐도, 쿼리 2번을 보면, k가 k번쨰 1번 쿼리까지 적용되었을 때의 구간합을 출력하라고 되어있습니다. 그냥 간단히 쿼리의 순서와 인덱스를 기억한다음에 출력해주는 오프라인 쿼리 방법을 생각해 볼 수 있었습니다.
import sys from math import ceil, log2 input = sys.stdin.readline def init(arr, tree, start, end, node): if start == end: tree[node] = arr[start] else: mid = (start + end) // 2 init(arr, tree, start, mid, node * 2) init(arr, tree, mid + 1, end, node * 2 + 1) tree[node] = tree[node * 2] + tree[node * 2 + 1] def update(tree, start, end, node, idx, add): if end < idx or start > idx: return tree[node] += add if start == end: return mid = (start + end) // 2 update(tree, start, mid, node * 2, idx, add) update(tree, mid + 1, end, node * 2 + 1, idx, add) def query(tree, start, end, node, idx_start, idx_end): if idx_end < start or idx_start > end: return 0 if idx_start <= start and idx_end >= end: return tree[node] mid = (start + end) // 2 return query(tree, start, mid, node * 2, idx_start, idx_end) \ + query(tree, mid + 1, end, node * 2 + 1, idx_start, idx_end) n = int(input()) arr = list(map(int, input().split())) h = ceil(log2(n)) tree_size = 1 << (h + 1) m = int(input()) # 세그먼트 트리와 lazy를 초기화한다. tree = [0] * tree_size # 세그먼트 트리 값 초기화 init(arr, tree, 0, n - 1, 1) ''' 먼저 쿼리를 모두 입력받고, k를 기준으로 정렬을 수행해야 하고, 다시 원래 순서대로 출력해야 한다. ''' queries_1 = [] queries_2 = [] q_idx = 0 for i in range(m): q, *args = map(int, input().split()) if q == 1: i, v = args queries_1.append((i, v)) elif q == 2: k, i, j = args queries_2.append((k, i, j, q_idx)) q_idx+=1 ''' 오프라인 쿼리 작용을 위해서 queris_2를 k를 기준으로 정렬해주어야 한다. ''' queries_2.sort(key = lambda x: x[0]) k = 0 ans = [0] * q_idx for i in range(len(queries_1)): ''' queries_2에서 k가 i보다 작은 경우에 대해 먼저 처리해주어야 한다. ''' while k < len(queries_2) and queries_2[k][0] <= i: _, qi, qj, q_idx = queries_2[k] ans[q_idx] = query(tree, 0, n - 1, 1, qi - 1, qj - 1) k += 1 idx, kk = queries_1[i] # idx에 대한 값을 가져온 다음에 2 -> 5면 5 - A[i]를 구한다음에 이를 update해주면 된다. kk -= query(tree, 0, n - 1, 1, idx - 1, idx - 1) update(tree, 0, n - 1, 1, idx - 1, kk) # arr[idx]를 v로 바꾼다. for i in range(k, len(queries_2)): _, i, j, q_idx = queries_2[i] ans[q_idx] = query(tree, 0, n - 1, 1, i - 1, j - 1) for i in range(len(queries_2)): print(ans[i])
여기서 kk - query() 이 부분은 쿼리1번을 처리해주기 위해 변화량을 더해주기 위한 일종의 trick입니다! 이전에 풀어본적이 있어서 간단히 구현할 수 있었습니다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ] - python 경찰차 (빡구현 + dp + dfs) (0) | 2023.07.01 |
|---|---|
| [BOJ] - python 열혈강호 (최대유량 + 이분매칭) (0) | 2023.06.30 |
| [BOJ] - python 스터디 그룹 (정렬 + 그리디 + 투포인터) (0) | 2023.06.30 |
| [BOJ] - 내 생각에 A번인 단순 dfs문제가 이 대회에서 E번이 되어버린 건에 관하여 (Easy) 극좌표압축 + 스위핑 + 완전탐색 + maximum subarray (0) | 2023.06.29 |
| [BOJ] - 제곱근 분할법 (Square Root Decomposition) + mo's 알고리즘 (0) | 2023.06.29 |
![[BOJ] - python 수열과 쿼리 21, 22 ( lazy propagation segment tree, offline query ) + Fenwick Tree](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FmVi1R%2Fbtsl2RUIdLz%2FgAE2ixnvaUR96aHrKixzk0%2Fimg.png)