https://www.acmicpc.net/problem/18251
18251번: 내 생각에 A번인 단순 dfs 문제가 이 대회에서 E번이 되어버린 건에 관하여 (Easy)
욱제는 🎄포화이진트리🎄를 종이에 그렸다. 노드에 정수 가중치도 채워 넣었다. 욱제는 적당한 직사각형 영역을 잡아서, 영역 내에 있는 노드들의 가중치 합을 최대로 하고 싶다. 직사각형은
www.acmicpc.net


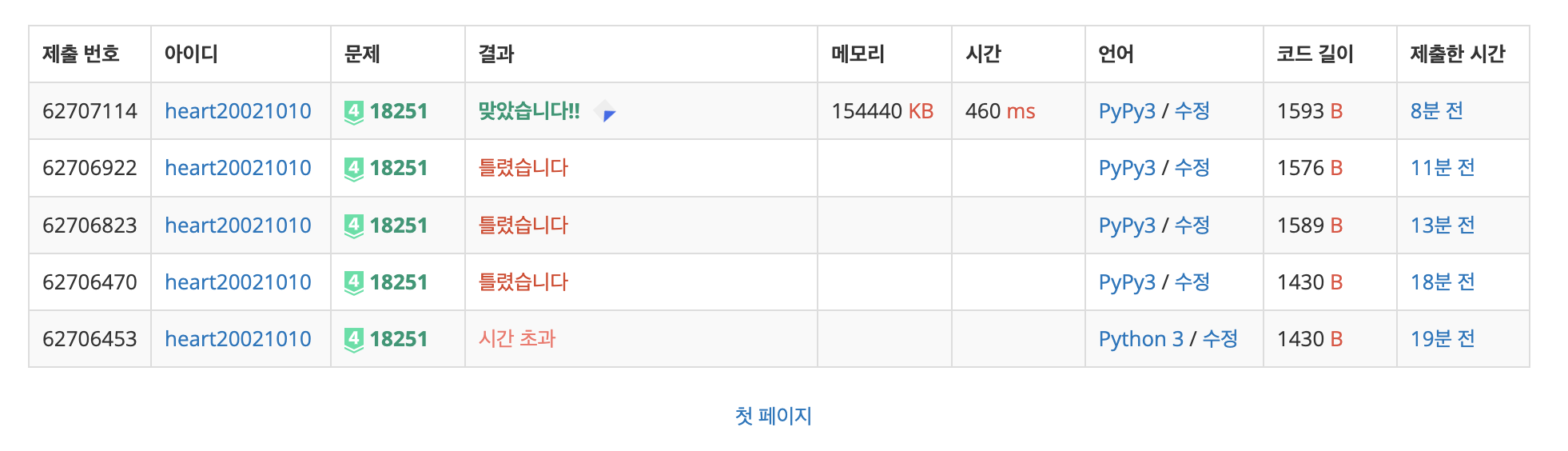
문제자체가 참 난감하다. 처음 든 생각은, 금광세그처럼 좌표를 압축한 다음에, 완전 탐색을 하는 것이였다. 그리고 잘 생각해보면, 2차원 스위핑을 1차원으로 치환할 수 있는데, dfs를 통해 각 노드에 시퀀스와 깊이를 저장해주면 이가 충분히 가능하다.
import sys input = sys.stdin.readline ''' 중위 순회 한 결과가 노드의 번호 순서가 될 것이다. ''' N = int(input()) node_seq = list(map(int, input().split())) # 해당 트를 기반으로 중위 순회를 해주어야 한다. # 높이를 저장할 배열 sweep_seq = [] def dfs(cur, d): if cur > N: return dfs(cur * 2, d + 1) sweep_seq.append((cur, d)) dfs(cur * 2 + 1, d + 1) ''' node_seq에서 dfs를 돈 sweep_seq에 저장한 (8, 3)의 의미는 node_seq[8 = (8번째로 방문한) - 1]의 노드에 대해서 깊이는 0,... (3)에 해당 ''' dfs(1, 0) ''' 스위핑을 하면서 maximum subarray를 모든 높이의 조합에 대해 구해주면 될거 같다. 모든 높이의 조합은 ''' max_depth = sweep_seq[-1][1] inf = 0x3f3f3f3f ans = -inf # 모든 노드가 음수인 경우 따로 처리해주어야 한다. for i in range(N): ans = max(ans, node_seq[i]) if ans <= 0: print(ans) exit(0) ans = 0 # print(sweep_seq) for i in range(max_depth + 1): # 모든 높이 조합에 대해서 스위핑을 하기 위함이다. for j in range(i, max_depth + 1): val = 0 for k in range(N): if sweep_seq[k][1] < i or sweep_seq[k][1] > j: # 스위핑 조건에 맞지 않으므로 배제한다. continue # 여기서부터 maximum subarray를 구해주면 되는 것이다. val = max(val + node_seq[sweep_seq[k][0] - 1], 0) # 0과 현재에서 더한것중에 큰 것을 선택한다 ans = max(ans, val) print(ans)
위 코드는 총 시간복잡도 O(Nlog^2(N))으로 해결했다. 그 이유는 높이가 최대 18까지밖에 안나오기 떄문에 모든 높이 조합에 대해서 완전 탐색을 하기 위한 시간복잡도는 log^2(N)이다. 그리고 그 다음에 마지막으로 maximum subarray 알고리즘 시간에 배운 개념을 통해서 O(N)으로 적용해주기만 하면 결과를 도출할 수 있게 된다.
주의할 점은 최소한 하나의 정점을 직사각형 안에 포함해야 해서, 모두 음수인 경우는 따로 처리해주는 방식으로 처리해주었다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ] - python 경찰차 (빡구현 + dp + dfs) (0) | 2023.07.01 |
|---|---|
| [BOJ] - python 수열과 쿼리 21, 22 ( lazy propagation segment tree, offline query ) + Fenwick Tree (0) | 2023.06.30 |
| [BOJ] - python 열혈강호 (최대유량 + 이분매칭) (0) | 2023.06.30 |
| [BOJ] - python 스터디 그룹 (정렬 + 그리디 + 투포인터) (0) | 2023.06.30 |
| [BOJ] - 제곱근 분할법 (Square Root Decomposition) + mo's 알고리즘 (0) | 2023.06.29 |
![[BOJ] - 내 생각에 A번인 단순 dfs문제가 이 대회에서 E번이 되어버린 건에 관하여 (Easy) 극좌표압축 + 스위핑 + 완전탐색 + maximum subarray](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcU6XRW%2FbtslOBMmY54%2FZsaE4EoflrpLKpbf4P7oB0%2Fimg.png)