문제
크기가 N인 정수 배열 A가 있고, 여기서 다음과 같은 연산을 최대 M번 수행해야 하는 문제가 있다고 해 봅시다.
1. 구간 l, r (l <= r)이 주어졌을 때, min(A[l], A[l+1], ..., A[r])을 구해서 출력하기
2. i번째 수를 v로 바꾸기 (A[i] = v)
1번째 연산 min(A[l], A[l+1], ... ,A[r])을 구하기 위해 소스 1과 같이 모두 더하는 방법이 있습니다.
소스1
ans = a[i] for i in range(l, r+1): if ans > a[i]: ans = a[i]
소스 1의 시간복잡도는 O(N)입니다. 2번 연산의 시간복잡도 A[i] = v는 O(1)입니다. 최대 쿼리가 M번 수행해야 하니 연산 하나의 시간 복잡도는 O(N)이 됩니다. 총 시간복잡도는 O(NM)입니다.
제곱근 분할법
제곱근 분할법을 사용하려면 크기가 N개인 배열을 크기가 sqrt(N)인 그룹으로 나누고, 각 그룹의 최솟값을 별도로 저장해야 합니다. 그룹의 크기가 sqrt(N)이니, 그룹의 개수도 sqrt(N)개입니다. N이 제곱수가 아닌 경우에는 그룹의 크기로 sqrt(N) <- 내림을 사용합니다. 그룹의 크기는 r, 그룹의 개수는 g, i번째 그룹에 들어있는 수의 최솟값은 D[i]로 표현합니다.

위와같은 예시에서 소스2를 통해 D를 구할 수 있습니다.
소스2
r = (int)(n ** 0.5) g = n // r if n % r != 0: g += 1 d = [0] * g for i in range(n): if i % r == 0: d[i//r] = a[i] else: if d[i//r] > a[i]: d[i//r] = a[i]
여기서 2번 연산은 i번쨰 수를 v로 바꾸는 연산입니다. 이 경우 i번째 수가 포함된 그룹의 D만 변경하면 됩니다. 그룹에 포함된 수의 최솟값을 구하려면, 그 그룹에 포함된 모든 모든 수를 조사하면 됩니다. 그룹에 포함된 수의 개수는 sqrt(r) <- 내림이니 시간 복잡도는 O(')가 됩니다.
소스3
def update(a, d, r, index, v): a[index] = v group = index // r start = group * r end = start + r if end > len(a): end = len(a) d[group = a[start] for i in range(start, end): if d[group] > a[i]: d[group] = a[i]
update(a, d, r, index, v)는 a[index]에 저장되어 있는 값을 변경하고, index가 해당하는 그룹의 최솟값도 변경하는 함수입니다. 변경을 구현하기 위해 먼저, a[index]에 저장되어 있는 값을 변경합니다. 그 다음, index가 속한 그룹의 번호를 구해 이를 group에 저장하고, 해당 그룹의 첫번째 인덱스 start와 마지막 인덱스 + 1인 end를 구합니다. 마지막으로 그룹에 들어있는 수 전체를 순회하면서 그룹의 최솟값 d[group]을 구합니다.
이제 마지막으로 예제를 하나 보고 mo's알고리즘에 대해 알아보겠습니다.

위 그림에서 [3~8]의 구간합을 구한다고 해보겠습니다. 구간 [4~6]은 그냥 2번째 그룹으로 대체할 수 있습니다. 즉, 직접 구해야 하는 것은 아래 그림과 같이 왼족과 오른쪽에 남아있는 원소들이 되겠습니다.

이는 쉽게 코드로 구현할 수 있을거 같습니다.
mo's 알고리즘
- 어떤 쿼리 (구간)에 대한 답을 구한다.
- 1번의 구간에서 앞부분의 구간을 더하거나 뺀다. 뒷부분의 구간을 더하거나 뺀다
- 2번 과정을 통해 다음에 구할 쿼리의 구간에 도달한다.
- 그 과정에서 다음 쿼리의 값을 계산한다.

위의 예시에서 (1, 2, 3, 4, 5, 6, 7, 8)인 크기 8의 배열이고 1~8의 구간합, 2~6의 구간 합, 3~7의 구간합을 차례대로 구하고 싶다고 가정합시다. 맨 처음 구간 합은 그냥 O(N)에 구할 수 있습니다. 그 전 구간의 크기를 0이라고 생각하고 구간 전체를 하나씩 더해가는 과정에서 구할 수 있습니다.
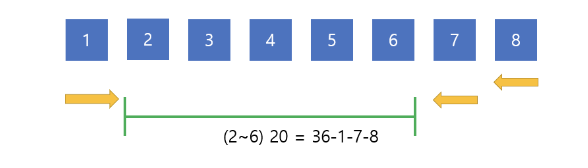
구간 (1~8)에서 구간 (2~6)으로 오기 위해서는 앞에서 1을 제거하고, 뒷부분에서 7과 8을 제거하면 됩니다. 그냥 앞에서부터, 뒤에서 부터 순서대로 제거하면서 숫자를 빼주면 36-1-7-8이 되면서 20이 나오게 되고 20은 현재 원하고자 하는 구간의 합, 즉 2~6에서의 구간합이 됩니다.
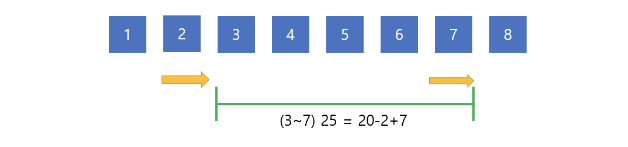
위의 과정에서 구한 구간 2~6에서 구간 3~7로 넘어가려면 앞쪽의 2를 빼고 뒷 쪽에 7을 붙이면 됩니다. 빼고 붙이는 과정에서 -2+7이 되기 때문에 3~7의 구간합은 25로 구해지게 됩니다.
시간복잡도는 한칸씩 움직일 때마다 O(1)이 걸리는 작업이라면 최악의 경우는 인접한 두 구역간에서 약 O(N)번을 움직여야 되고 한 개의 쿼리를 처리하는데 O(N)이 걸리게 됩니다. 따라서 구간들을 최대한 잘 조정해서 구간간의 변화에 따른 이동을 최소화 해야 합니다. 이를 쿼리를 잘 정렬함으로써 해결할 수 있고, 그 쿼리의 구간(l, r)에 대해서 정렬방법은 다음과 같습니다.
- sqrt(N)에 대해서 먼저 정렬합니다.
- 1의 값이 같은 구간의 쿼리에 대해서 r에 대해서 정렬만 하면 됩니다.
위와같이 정렬을 한다고 했을 때, 1번 정렬에 의해서 쿼리들이 sqrt(N)개의 그룹으로 나뉘어질것이고. 각 그룹에 대해서는 r이 계속 증가하기 때문에 O(N)만큼 움직입니다.
13547번: 수열과 쿼리 5
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. i j: Ai, Ai+1, ..., Aj에 존재하는 서로 다른 수의 개수를 출력한다.
www.acmicpc.net
위의 예시는 오프라인쿼리와 mo's 알고리즘을 활용한 백준 문제 입니다.

i, j라는 쿼리에 대해서 서로 다른 수의 개수를 출력하면 됩니다. 이는 사실 제가 이전에 풀었던 머지소트 트리를 통해서도 O(log^2N)으로 해결할 수 있지만, mo's 알고리즘을 배웠으니 이를 활용해서 풀어보도록 하겠습니다.
다시 mo's 알고리즘을 되세겨보면, 쿼리의 i, j가 있을 때 쿼리의 순서를 (i//sqrt(N), j)의 우선순위로 더 작은 것을 먼저 처리합니다. (i//sqrt(N))에서 sqrt(N)은 평방분할에서 나온 것입니다. 전체 N개의 수열을 sqrt(N)개의 그룹으로 나누면 각 그룹은 대표값과 sqrt(N)개의 값을 가지게 됩니다. 세그먼트 트리처럼 그룹의 대표값을 구하고 싶은 범위 안에 그룹이 있다면 그룹 내의 모든 값들을 탐색하지 않고 그룹의 대표값만 탐색하여 시간을 줄이는 방식입니다.
쿼리를 정렬하는 방식에서 평방분할을 사용하는 방법은 구간이 여러개가 있을 때, 시작과 끝 범위가 계속해서 달라지므로 시작과 끝을 +=1, -=1시키며, 계속 변경하며 탐색할텐데 여기서 모든 쿼리를 탐색할 때 변경되는 정도를 최소화하기 위해서입니다. 평방분할을 사용해 쿼리를 정렬하고 시작과 끝을 변경시키면서 탐색하면, 시작과 끝을 변경하는 횟수를 N * sqrt(N)으로 최소화 할 수 있게 됩니다.
start는 최대 sqrt(N) * sqrt(N)번으로 N번 움직일 수 있고, end는 최대 N * sqrt(N) - 0.5*sqrt(N) ~= 0.5 * N * sqrt(N)번 움직일 수 있습니다. 그래서 총 시간 복잡도는 N + 0.5N(sqrt(N)) ~= N*sqrt(N)이 되는 것입니다.
import sys input = sys.stdin.readline ''' i~j까지의 서로 다른 값들을 d_set에 저장해주었다. 중복되는 수가 있다면 그 수의 갯수의 값으로 저장한다. ''' def query(start, end, cache): if cache: # 캐시를 통해 이전 쿼리의 정값을 얻어주어야 한다. d_start, d_end, d_set = cache while d_end < end: d_end += 1 if nums[d_end] in d_set.keys(): d_set[nums[d_end]] += 1 else: d_set[nums[d_end]] = 1 while d_end > end: d_set[nums[d_end]] -= 1 if d_set[nums[d_end]] == 0: del d_set[nums[d_end]] d_end -= 1 while d_start > start: d_start -= 1 if nums[d_start] in d_set.keys(): d_set[nums[d_start]] += 1 else: d_set[nums[d_start]] = 1 while d_start < start: d_set[nums[d_start]] -= 1 if d_set[nums[d_start]] == 0: del d_set[nums[d_start]] d_start += 1 cache = (d_start, d_end, d_set) return len(d_set), cache else: d_set = {} for i in range(start, end+1): if nums[i] in d_set.keys(): d_set[nums[i]] += 1 else: d_set[nums[i]] = 1 cache = (start, end, d_set) return len(d_set), cache N = int(input().rstrip()) nums = list(map(int, input().split())) M = int(input().rstrip()) sqrt = N**0.5 queries = [] for i in range(M): s, e = map(int, input().split()) queries.append((s - 1, e - 1, i)) # idnex까지 저장해준다. # 쿼리를 (i//sqrt(N), j)의 우선순위로 mo's 알고리즘을 적용해주기 위해 immutable을 지켜주면서 정렬해준다. queries = sorted(queries, key=lambda x: (x[0]//sqrt, x[1])) ans = [0] * M cache = 0 for q in queries: s, e, idx = q cnt, cache = query(s, e, cache) ans[idx] = cnt for i in ans: print(i)
사실 이는 위에서도 말했지만 머지소트 트리를 사용하면 매 쿼리마다 O(logN)으로 해결되서 O(NlogN)으로 해결가능하다.
여기서는 d_set{}의 딕셔너리 형태로 서로 다른 값들을 저장해주었습니다. dict에 서로 다른 수를 key로 저장하고, 중복되는 수가 있다면 그 수의 갯수를 값으로 저장해주었습니다. 추가 할 때는 해당 키가 있으면 +=1, 없으면 값을 1로 할당하여 딕셔너리에 할당해주었습니다. 만약 해당 범위에서 수가 사라져 삭제하면 -=1해주고, 값이 0이면 그 수가 없다는 것이므로 키를 삭제해 버렸습니다. 이렇게 하면 d_set의 길이를 구하면 서로 다른 수의 개수를 얻을 수 있습니다.
먼저 쿼리를 처음 수행할 떄에는 이전의 쿼리가 없으므로 naive하게 s~e까지 탐색을 해가며 d_set을 구했습니다. 이전의 (start, end, d_set)을 캐시로 저장하여 다음 쿼리에서 사용할 수 있도록 넘겨주었습니다. 다음 하수는 cache를 통해 이전 쿼리의 시작, 끝, 딕셔너리 정보를 d_start, d_end, d_set으로 얻을 수 있고, 이를 바탕으로 d_start는 start와 일치할 때까지, d_end는 end와 일치할 때까지 변경시켜 가며 d_set을 수정했습니다.
d_end를 먼저 변경해주는 이유는 우리가 쿼리를 정렬할 때 오름차순으로 정렬하였기 때문에 (1,1) (3,3)등의 쿼리가 있을 때 d_start를 먼저 변경하면 (1,1) -> (2,1) -> (3,1)이렇게 start보다 end가 작은 상황이 발생할 수 있어서. 이런 현상을 막기 위해 d_end부터 변경해주었습니다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ] - python 경찰차 (빡구현 + dp + dfs) (0) | 2023.07.01 |
|---|---|
| [BOJ] - python 수열과 쿼리 21, 22 ( lazy propagation segment tree, offline query ) + Fenwick Tree (0) | 2023.06.30 |
| [BOJ] - python 열혈강호 (최대유량 + 이분매칭) (0) | 2023.06.30 |
| [BOJ] - python 스터디 그룹 (정렬 + 그리디 + 투포인터) (0) | 2023.06.30 |
| [BOJ] - 내 생각에 A번인 단순 dfs문제가 이 대회에서 E번이 되어버린 건에 관하여 (Easy) 극좌표압축 + 스위핑 + 완전탐색 + maximum subarray (0) | 2023.06.29 |
![[BOJ] - 제곱근 분할법 (Square Root Decomposition) + mo's 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcKCvoW%2FbtslMWPA2bI%2Faz1bcIkxwFqKlrE3hZUQP1%2Fimg.png)