[딥러닝 최신 트렌드 알고리즘] - Feedforward Network

Feed-forward란 다층 퍼셉트론MLP, CNN, self-attention등에서 다양한 분야에서 사용됩니다. 이는 비선형적으로 input을 바꿔 아웃풋을 생각하는 파라미터weight를 학습할 수 있는 연결된 뉴런으로 구성된 시스템을 말합니다.

결과적으로 비선형 or 선형인 activation function을 사용해서 이를 다른 좌표계로 변형하는 과정을 말하게 됩니다. 즉 앞단에서 선형적으로 Weight, bais같은 걸 받아서 affine transform(선형 변환)을 받은 뒤 활성 함수등으로 non-linear변형을 합니다. 

 

tanh 활성화 함수

sigmoid는 0~1로 값을 압축해주었었습니다. 그래서 미분을 하더라도 local minimum에 빠지게 될 수 있습니다. 하지만 tanh는 -1~1로 값을 압축해서 0이 중심이기 때문에 sigmoid와 같은 bais shift가 없다는 장점이 있습니다. 하지만 이는 sigmoid와 같은 Saturation문제인 gradient vanishing문제가 존재합니다.

 

ReLU 활성화 함수

매우 간단하게 생겼습니다. max(0, z)로 표현될 수 있습니다. 이는 일단 매우 쉽게 미분할 수 있습니다. 그리고 Sparsity즉 희박하게 뉴런을 활성화 시킬 수 있습니다. 즉 값이 0인 부분이 많으므로 많은 연산이 줄어든다는 장점이 있습니다. 또한 Saturation 문제가 발생하지 않습니다. 

 

하지만 이는 값이 unbounded합니다. 그리고 0이 중심이 아니며 Dying ReLU문제가 발생할 수 있습니다. Layer가 아주 깊거나 learning rate등이 잘못세팅되면 용량을 차지하거나 항상 죽어있는 문제가 발생할 수 있습니다. 이 경우도 gradient vanishing!! 즉 이는 Generalize된 ReLU함수를 쓰면 조금 해결됩니다.

 

Leaky ReLU 활성화 함수

이를 사용하면 퍼포먼스적으로 조금 손해를 볼 수 있으나 saturation문제나 Dying ReLU문제를 어느정도 해결할 수 있다는 장점이 있습니다. 하지만 이는 ReLU대비 데이터가 작을 때 오버피팅이 일어날 수 있는데, ReLU가 데이터가 적을 때 어떠한 Feature를 죽일건 죽이는 그러한 특징이 있었는데, 그러지 못하니까 Feature가 많아지게 되어 오버피팅 될 수도 있다는 것입니다.

 

ELU (exponential Linear Unit) 활성화 함수

이는 Leaky ReLU보다 더 자연스럽게 변화시킨다는 장점이 있습니다. 이는 일반적인 상황에서 가장 효과가 좋습니다. 그리고 모든 경우에서 미분 가능하다는 장점이 있습니다. 그리고 convex형태를 띄게 할 수 있어 효과를 가질 수 있게 할 수 있습니다.

 

즉 ANN을 최적화 하기 위한 목적함수, 즉 비용 함수(cost function)는, 보통 가능도 함수를 최대화 (maximum likelihood)를 하는 방법을 선택합니다. x, y~pdata이고 (x가 인풋, y가 아웃풋(라벨)), 세타가 학습 가능한 파라미터일 때 모델이 추론하는 확률 분포를 q(y|x. 세타)라고 하겠습니다. 여기서 q(y|x, 세타)는 조건부 확률 분포를 의미합니다. 입력 x와 어떤 모델 파라미터 세타가 주어졌을 때 출력 y에 대한 모델의 예측 확률 분포를 의미합니다. 따라서 위 경우에서 가능도를 최대화하는 세타를 찾는 것은 주어진 데이터를 가장 잘 설명하는, 즉 모델이 데이터가 가장 잘 적합하는 세타를 찾는 것과 같습니다. 이는 모델의 학습 과정 중에서 비용 함수 또는 손실 함수를 최소화하는 것과 같은 맥락입니다!

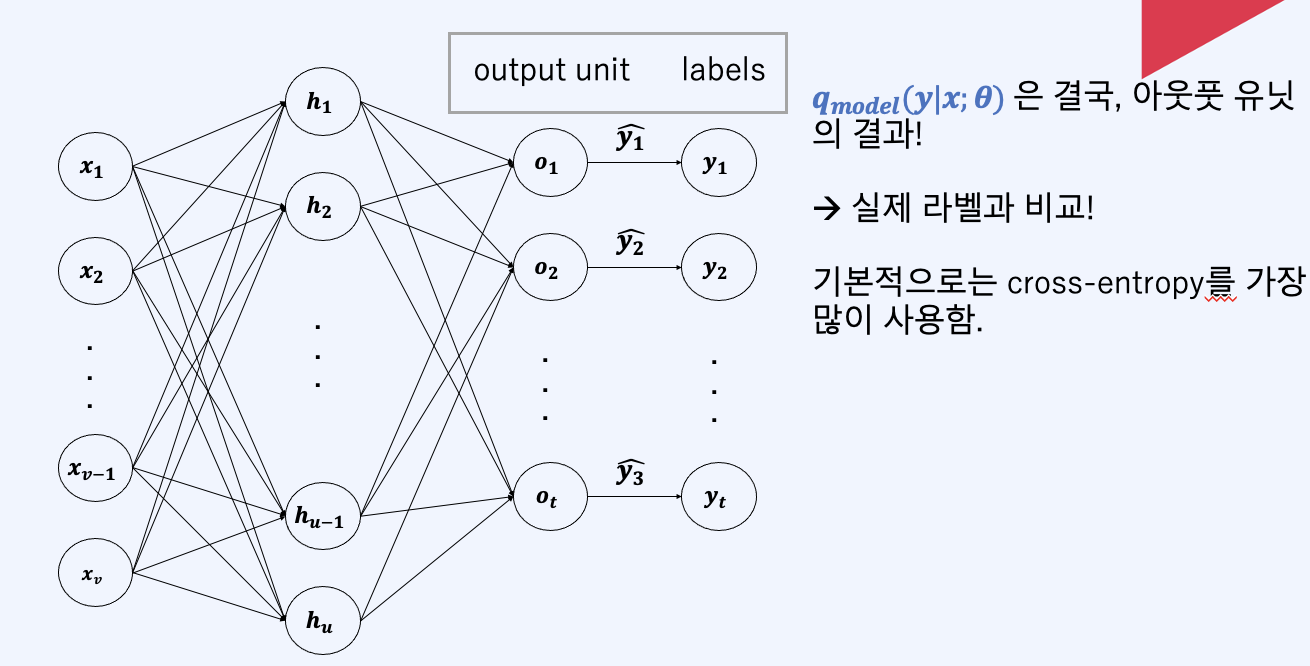
즉 우리는 실제 y^(실제 라벨)과 Qmodel(y|x, 세타)를 비교해서 크로스 엔트로피(목적 함수)를 줄여나가는 방식으로 학습을 진행합니다.

output unit

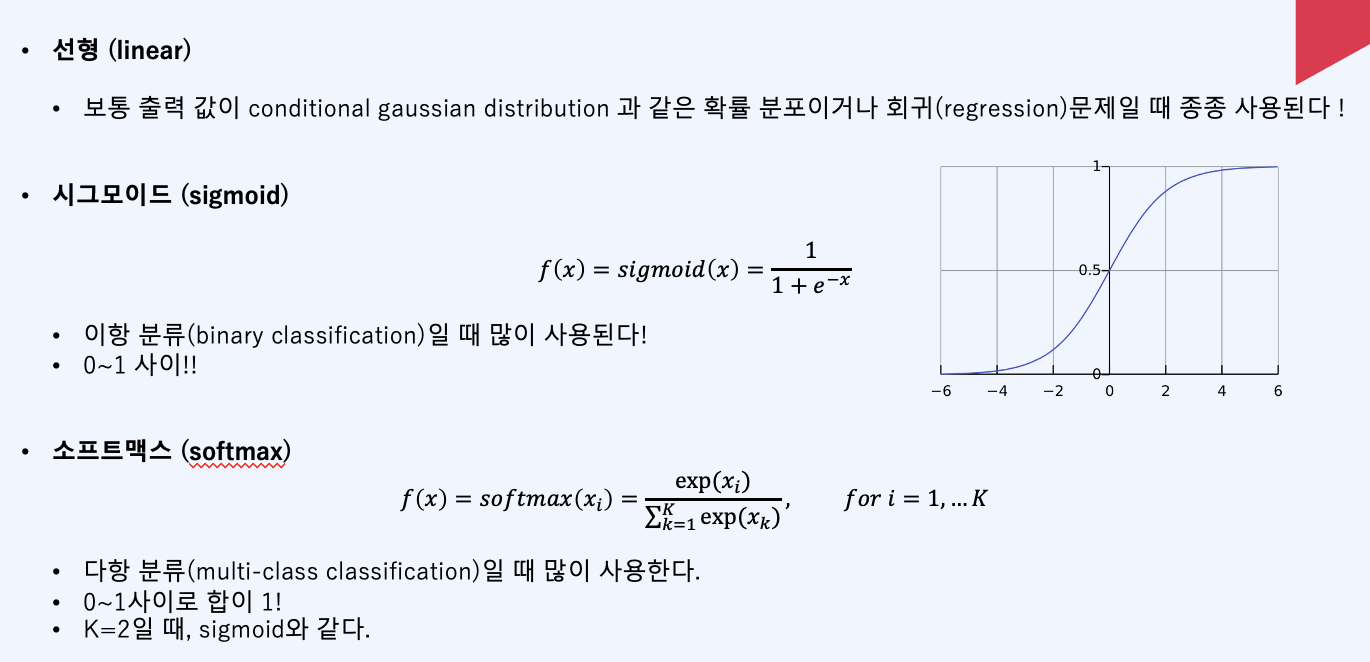
그리고 어떤 output unit이란 값을 마지막에 정제하는 역할을 합니다. 일부러 정제를 안하는 경우가 있는데, 출력 값이 conditional gaussian distrubution과 같은 확률 분포인 경우가 있을겁니다. 그리고 앞에서 ReLU를 앞단에서 사용한다면 맨 마지막에 시그모이드를 output unit에 사용하는 경우도 있습니다. 그 이유는 시그모이드가 확실한거는 그냥 확 올려버리기 때문입니다. 이 시그모이드를 이항분류(binary classification)에 많이 사용된다면, muti-class classification일 때는 소프트맥스(softmax)를 주로 사용합니다.

그리고 혼합밀도도 사용할 수 있는데, 이는 불확실성 자체를 출력으로 나타내주기 위한 방법중이 하나입니다. 이는 XAI등에서 사용됩니다.

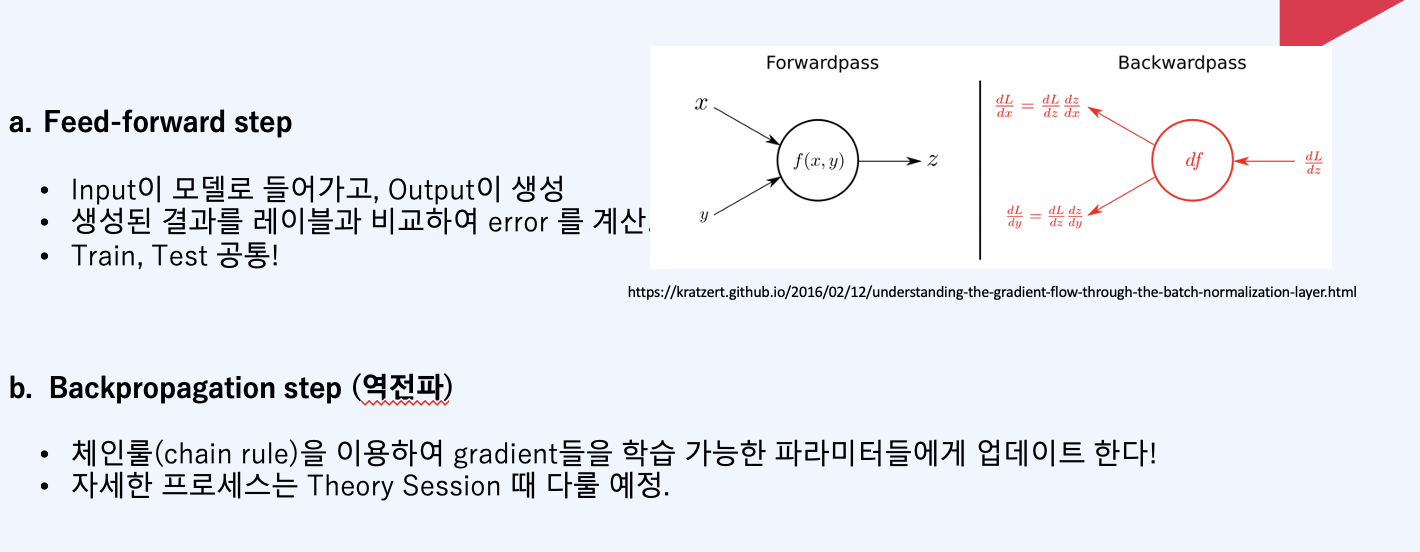
실제 Feed-forward, Backpropagation step을 우리가 실습해 볼 내용이기도 합니다. Feed-forward는 Train, Test모두 진행하며, 이는 생성된 결과를 레이블로 비교해서 error를 비교합니다. 반면에 backpropagation은, chain rule을 통해 gradient들을 학습 가능한 파라미터들에게 업데이트를 하는 것을 말합니다.

그리고 각 forward step은 on-line에서 학습을 진행시켜야 하기 때문에 이는 서비스 퍼포먼스에 직결됩니다. 반면 Backward step은 Online으로 학습을 돌리는 상황이 적기 때문에 이는 서버 퍼포먼스에 큰 영향을 끼치지 않습니다. 그리고 MLP의 경우 컴퓨터이션 코스트는 행렬의 곱 형태로 계산됩니다. forward step에서 weight matrix를 더하기 위해서는 O(w), Backward step에서도 O(w)이 듭니다. 메모리 코스트는 미니베치의 예제수가 m이고 h가 은닉층 유닛의 개수라면 O(mh)가 됩니다. 이와같은 병렬적인 컴퓨팅때문에 GPU를 사용하면 일반적으로 빨라진다는 것입니다.