![[딥러닝 최신 알고리즘] - 정보이론 (엔트로피, KL 발산, 크로스 엔트로피)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbcLaNx%2FbtslboUI0gW%2FkLAqQ3EFLKda0pT8EQWUV0%2Fimg.png)
ML을 공부하다 정보이론 내용이 수식이 어려워서 한번 정리해보면 좋을거 같아 정리합니다.
어떤 정보는 특정한 관찰에 의해 얼마만큼의 정보를 획득했는지 수치로 정량화 한 값입니다. 사건 A가 발생할 확률을 P(X)라고 할 때 정보량은 -logP(X)라고 표현할 수 있습니다.
반면 엔트로피는, 변수의 불확실성을 나타내는 지표로서, 확률분포 p를 가지는 변수X에 대해서 위와같이 표현할 수 있게 됩니다. X가 특정한 값을 가질 확률이 1인 경우에 엔트로피는 최솟값이 됩니다. 이때의 엔트로피의 값은 0입니다. 즉 불확실성이 감소할 수록 엔트로피의 값은 작아집니다. 반대로 각 값을 가질 확률이 다 같은 경우 엔트로피의 값은 최대가 됩니다.
KLD는 2개의 확률분포가 어느 정도 닮았는지를 나타내는 척도를 말합니다. 이에 대한 이산확률분포에서 정의는 위와 같습니다. 여기서 어느 정도 닮았는지는, 엔트로피의 차이를 통해 계산됩니다. 위의 최종식을 보면, H(P, Q) - H(P)라고 표현되어 있습니다. 그리고 이는 잘보면 우리가 예측한 모델의 확률분포인 (pi)log(qi)의 엔트로피의 값들에서 실제 라벨의 엔트로피의 값인 (pi)log(pi)의 값을 뺀 것이 DKL(P||Q)라고 할 수 있겠습니다. 이는 Jenson Inequality를 통해 증명될 수 있습니다. 그리고 교환법칙이 성립하지 않으며 많은 성질들이 존재합니다.
Cross entropy, H(p, q)를 전개해보면 그 안에 이미 확률 분포 p의 엔트로피가 들어 있습니다. 그 H(P)에 무언가 더해진 것이 cross entropy입니다. 이때 이 무언가 더해지는 것이 바로 "정보량 차이"인데, 이 정보량 차이가 바로 KL-divergence입니다. 직관적으로 정리를 하면 KL-divergence는 p와 q의 cross entropy에서 p의 엔트로피를 뺀 값입니다. 결과적으로 우리가 맨 위에서 본 식이 유도가 되는 것입니다.
결국 Cross Entropy는 negative log likelihood와 같습니다. 그래서 cross entorpy를 minimize하는 것이 log likelihood를 maximize하는 것과 같게 됩니다. 그리고 확률분포 p, q에 대한 cross entorpy는 H(p) + KL(p|q)이므로 KL-divergence를 minimize하는 것 또한 log likelihood를 maximize하는 것과 같다는 소리가 됩니다.
cross entorpy를 수식으로 적어보면 위와 같습니다. 대개 머신러닝에서는 cross entropy를 사용할때는 아래와 같습니다. pi가 특정 확률에 대한 참값 또는 목표 확률이고 qi가 우리가 현재 학습한 확률값입니다. 예를 들어 여기서 p = [0.5, 0.125, 0.125, 0.25]이고, q = [0.25, 0.25, 0.25, 0.25]가 되는 셈입니다. 따라서 우리가 어떤 qi를 학습하고 있는 상태라면 pi에 가까워질수록 cross entorpy의 값은 작아지게 됩니다. 이러한 특성 때문에 cross entropy를 머신러닝에서 많이 쓰는 것입니다. 이산형이 아니라 연속형인 확률분포에서는 시그마가 아니라 integral이 들어오게 되는 점이 다릅니다. -> 이 cross-entropy함수는 convex이기 때문에 gradient descent와 같은 걸로도 최적화가 가능해지게 됩니다.
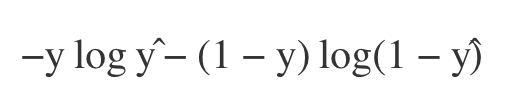
위는 우리가 대개 logistic regression에서 보는 cost function입니다. Binary classification에서는 0 또는 1로 두 가지 class를 구분합니다. 우리가 어떤 대상이 1이라고 predict(또는 분류)하는 확률qy=1를 y^(hat)이라고 놓겠습니다. 그렇다면 어떤 대상을 0으로 predict하는 확률은 1-y^가 됩니다. !! 잘 보면 logistic regression의 cost function은 단순히 우리가 위에서 봤든 cross entropy의 sigma를 풀어 쓴 것에 불과했다는 것을 깨닳을 수 있게 됩니다.
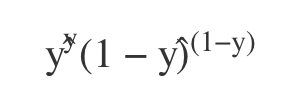
그리고 cross entropy는 log loss로도 불리는데, 왜냐면 cross entropy를 최소화하는 것은 log likelihood를 최대화하는 것과 같기 때문입니다. 어떤 데이터가 0 또는 1로 predict될 확률은 y^, 1-y^로 표현가능하기 때문에, likelihood식을 위와같이 세워볼 수 있게됩니다.
y=1일때 y^를 최대화시켜야 하고 y=0일떄는 1-y^를 최대화해야 합니다. 여기에 log likelihood가 작아지기 때문에 cross entropy값을 작게 해야합니다.
여기서 잠깐 likelihood의 개념을 다시 짚고 가면
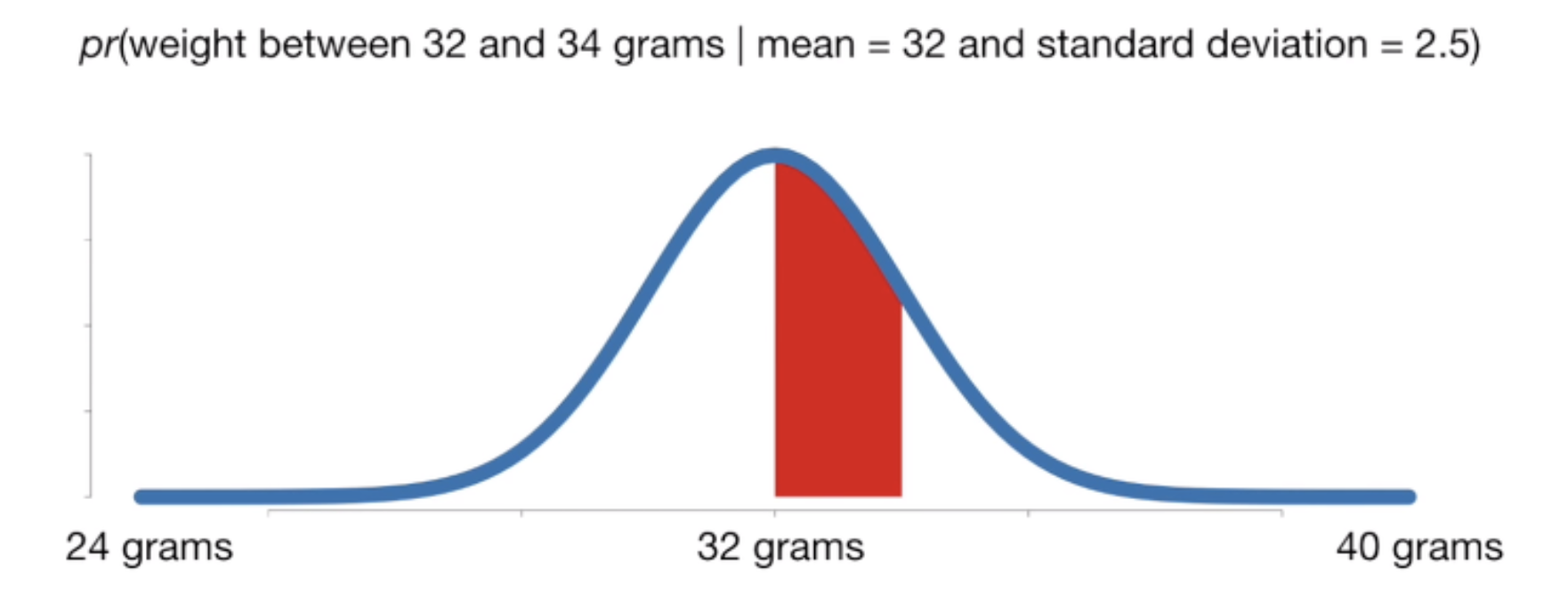
이는 쥐의 무게가 정규분포(m=32/sd=2.5)를 따르는 것을 나타낸 것입니다. 일단 가능도(Likelihood)란 L(확률분포D | 관측값X)입니다. 즉 만약 내가 쥐를 뽑아서 무게를 달았는데 34g이 나왔다고 하자. 이때 관측 결과가 정규분포(')에서 나왔을 확률은 0.12이고 이것이 가능도라고 하는 것이다. 즉 관측 값이 고정되고, 그것이 주어졌을 때 해당 확률분포에서 나왔을 확률을 구하는 것입니다. 그리고 MLE는 어떠한 관측된 값들이 있을때 (Pdata) 이 우도들의 합을 최대화 하는 것인 최대 우도 측정을 말하는 것이라고 할 수 있다!