![[ 딥러닝 최신 기술 ] - Adversarial Training, Data augmentation](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FtppZJ%2Fbtspnj8qd37%2FkeNb09vmyZ9rtKnSyb0b0K%2Fimg.png)
Adversarial Training
위와같이 어떤 판다에 대한 57.7%의 confidence를 가지는 결과에 0.007의 가중치를 주어 "nematode"라는 noise를 주어보았습니다. 그랬더니 결과물은 전혀 다른 결과인 "giboon"이라는 99.3%의 신뢰도를 가지는 결과가 나오게되었습니다.
이는 입력은 아주 조금 바뀌었으나, 출력이 매우 달라지며, 그때의 기울기가 매우 가파른 경우로 일종의 오버피팅 상태라고 할 수 있습니다. 이러한 현상을 생각해 일종의 노이즈를 섞어 학습을 진행한다면 이는 어떻게 보면 Regularization의 효과가 나오게 될 것입니다.
우리가 각 인풋을 노이즈를 섞어 $\epsilon$만큼 바꿀 때, $\epsilon\|w\|_{1}$변화한다고 할 수 있습니다. 이 때, w가 만약 높은 차원이라면 그 값은 매우 커질 수 있겠습니다. 적대적 학습은 로컬 상수 값(노이즈)를 추가한 데이터를 학습하며 이러한 "locally linear behavior"로 인해 생기는 네트워크의 민감성(sensitivity)를 줄일 수 있게 됩니다.
그래서 fast gradient 방법은, 아래와 같은 만들어진 데이터를 생성할 수 있습니다. $w^T x ̃=w^T x+w^T η$, $η=ϵsign(∇_x J(w))$ 즉 w근처에서 gradient에 선형 값에 linear벡터 값을 인풋값에 더해 adversarial example을 생성하는 것입니다.
Data Augmentation
데이터 증강(=Data Augmentation)은 기존에 머신러닝때부터 유명한 방법이였습니다. 이를 적용하면 위와같이 Top-1 accuracy, Top-5 accuracy등이 다 기본적으로 올라가는 것을 볼 수 있습니다. 그래서 목적에 맞는 데이터 증강방법을 사용하는 것이 핵심입니다.
또한, 기본적인 방법 외에도 위와같이 고양이와 양 사진을 짬뽕한 사진을 사용해도, 놀랍게도 성능이 올라갑니다.
또한 위와같이, 구멍을 내도 일반화 성능을 높일 수 있게됩니다.
일반 ERM은 두 클래스간의 decision boundary가 매우 뚜렷하여 정확하게 분리됩니다. 이는 오버피팅의 위험이 큽니다. 하지만 mixup을 통해 beta distribution을 적용시켜주게 되면, 두 클래스 간의 decision boundary가 ERM에 비해서 부드럽게 됩니다. 이는 mixup이 ERM에 비해서 과적합이 덜 발생한다는 것입니다.
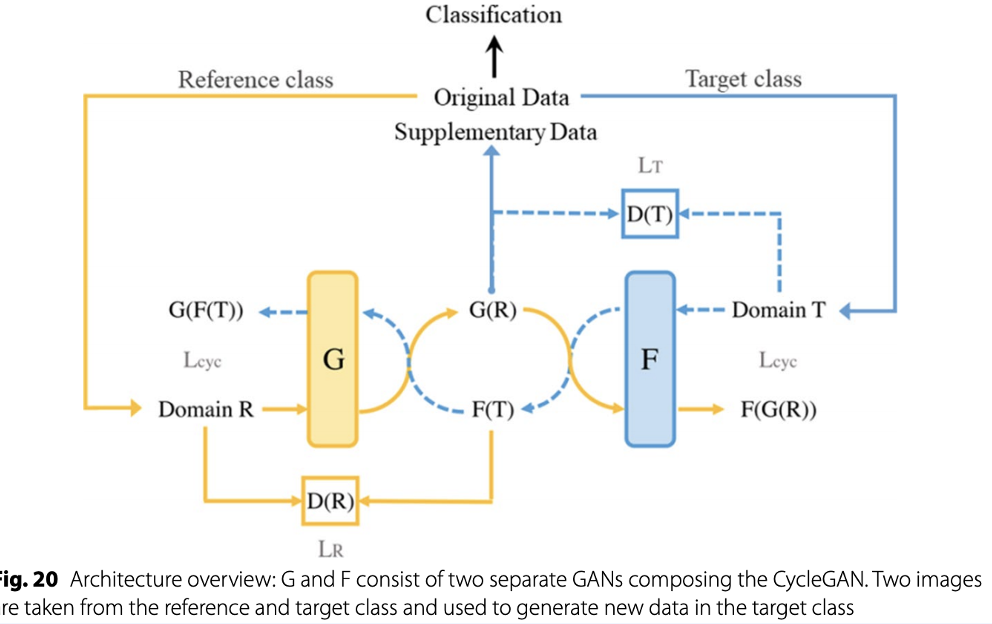
또한 모델을 통해서 데이터 증강을 할 수 있는데, 이는 GAN과 같은 최신 기술로 이미지 내에서 interpolation을 수행하여 샘플링을 하는 방법을 의미합니다.
사실 위 내용들은 Regularization을 공부하며 정리한 것입니다. 이 외에도 Norm기반, 앙상블기반, Dropout, Early-Stopping, Parmameter-Sharing, Multi-task Learning등 여러 방법이 있습니다. 이 중 Dropout, Early-Stopping은 직접 실습을 하며 알아볼 계획이고, 나머지 내용은 추후에 논문이나 내용을 정리하며 추가적으로 설명할 계획입니다.