1. 힙 (Heap) 이란?
- 힙: 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리 (Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
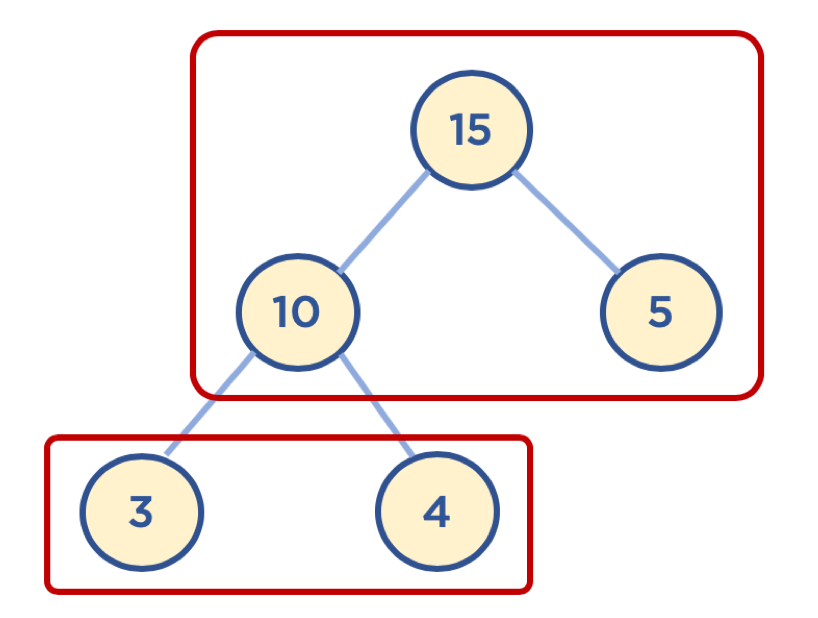
- 힙을 사용하는 이유 - 배열에 데이터를 넣고, 최댓값과 최솟값을 찾으려면 O(n)이 걸림 - 이에 반해, 힙에 데이터를 넣고, 최댓값과 최솟값을 찾으면 O(log n)이 걸림 - 우선순위 큐와 같이 최댓값 또는 최솟값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨
2. 힙 (Heap) 구조
- 힙은 최댓값을 구하기 위한 구조 (최대 힙, Max Heap)와, 최솟값을 구하기 위한 구조 (최소 힙, Min Heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
- 각 노드의 값은 해당 노드의 자식노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 합의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
- 완전 이진 트리 형태를 가짐
- 각 노드의 값은 해당 노드의 자식노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
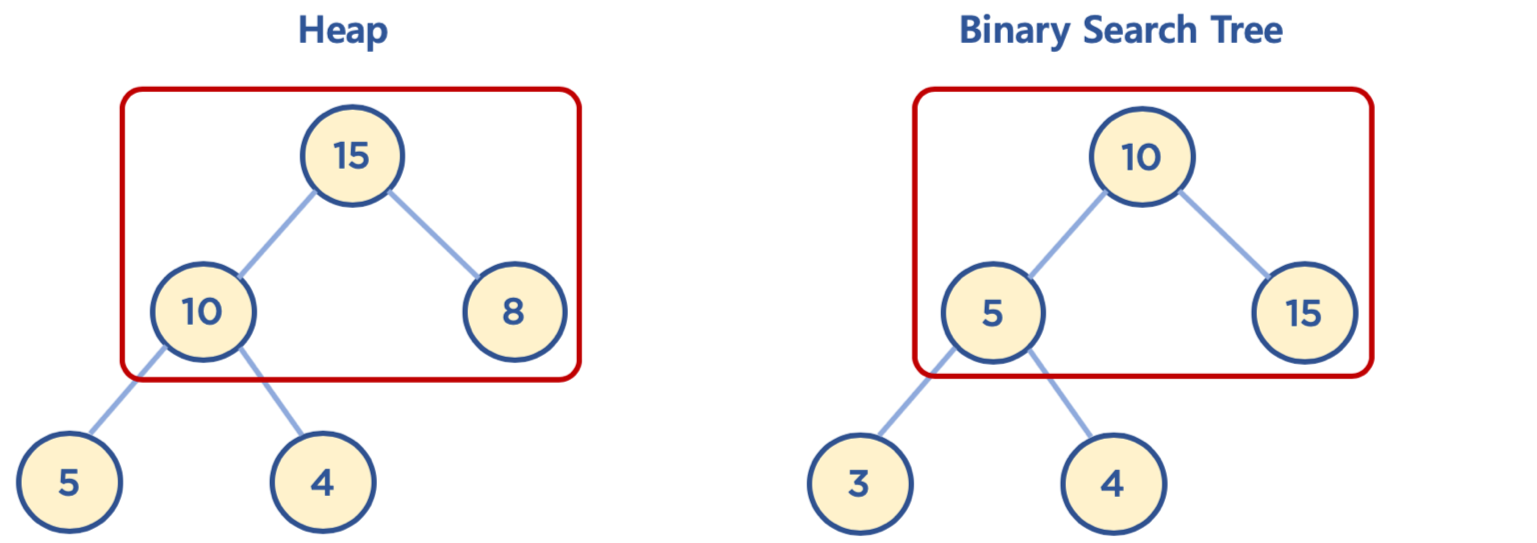
힙과 이진 탐색 트리의 공통점과 차이점
- 공통점: 힙과 이진 탐색 트리는 모두 이진 트리임
- 차이점:
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음 (최대 힙의 경우)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
- 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 힙의 왼쪽 및 오른쪽 자식 노드의 값은 오른쪽이 클 수도 있고, 왼쪽이 클 수도 있음
- 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨
3. 힙 (Heap) 동작
- 데이터를 힙 구조에 삽입, 삭제하는 과정을 그림을 통해 선명하게 이해하기
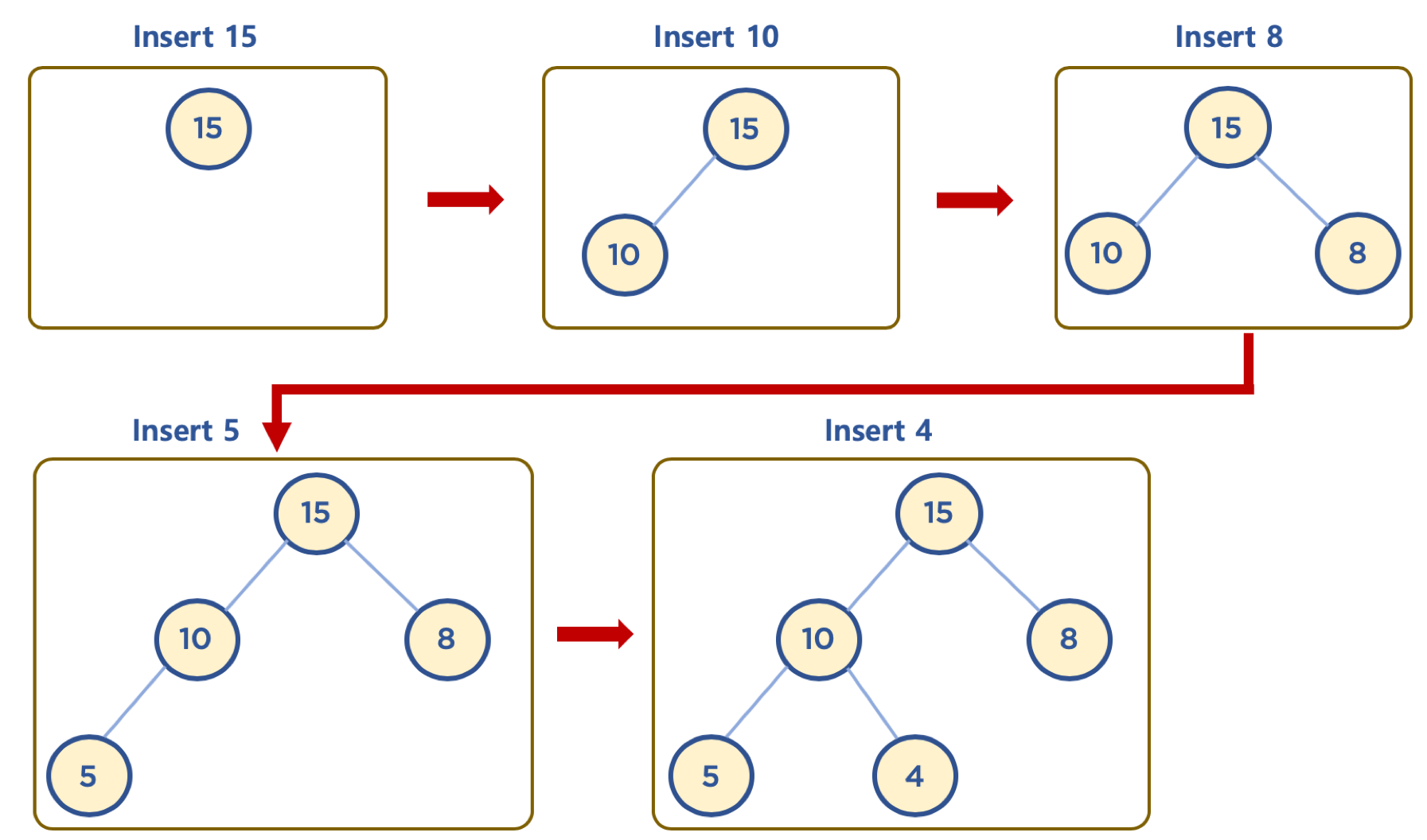
힙에 데이터 삽입하기 - 기본동작
- 힙은 완전 이진 트리이므로, 삽입할 노드는 기본적으로 왼쪽 최하단 노드부터 채워지는 형태로 삽입
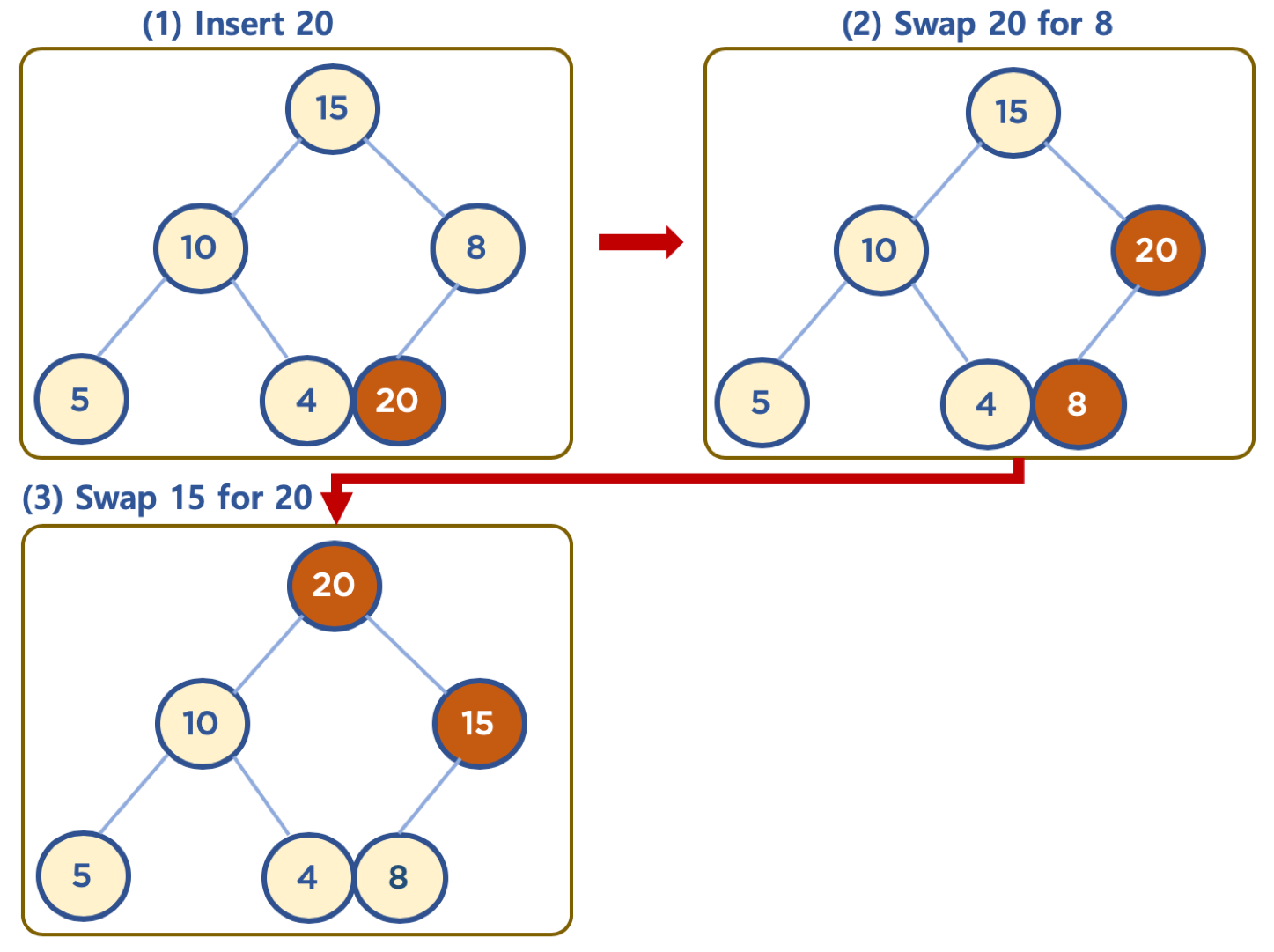
힙에 데이터 삽입하기 - 삽입할 데이터가 힙의 데이터보다 클 경우 (Max Heap의 예)
- 먼저 삽입된 데이터는 완전 이진 트리 구조에 맞추어, 최하단부 왼쪽 노드부터 채워짐
- 채워진 노드 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복함 (swap)
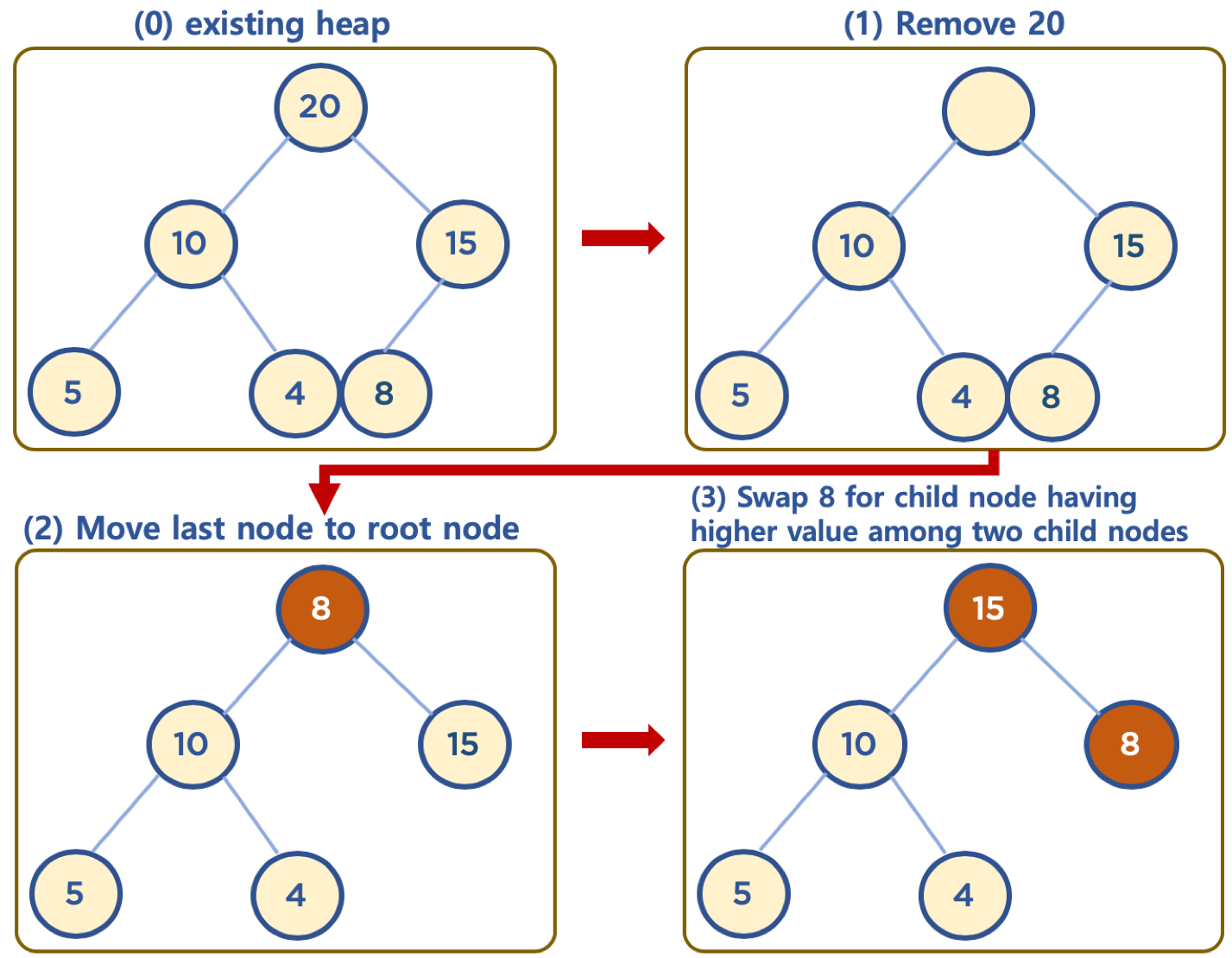
힙의 데이터 삭제하기 (Max Heap의 예)
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최댓값 또는 최솟값을 root노드에 놓아서, 최댓값과 최솟값을 바로 꺼내 쓸 수 있도록 하는 것임
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드)를 root노드로 이동
- root노드의 값이 child node보다 작을 경우, root노드의 child node중 가장 큰 값을 가진 노드와 root노드 위치를 바꿔주는 작업을 반복함 (swap)
4. 힙 구현
힙과 배열
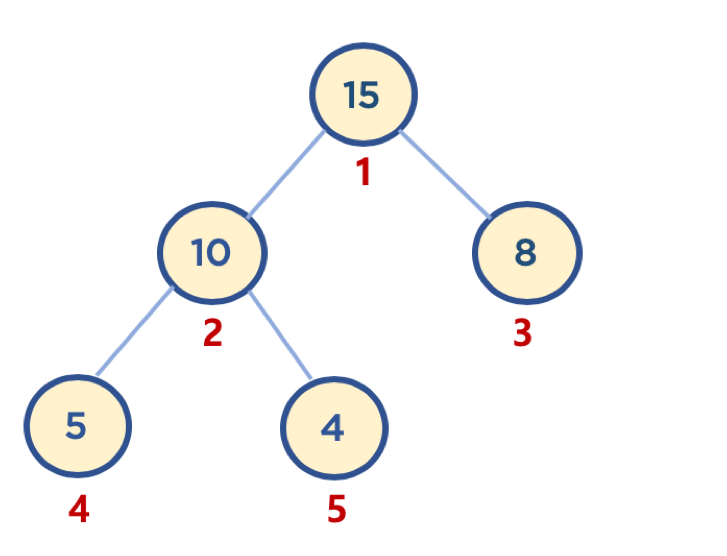
- 일반적으로 힙 구현시 배열 자료구조를 활용함
- 배열은 인덱스가 0번부터 시작하지만, 힙 구현의 편의를 위해, root노드 인덱스 번호를 1로 지정하면, 구현이 좀더 수월함
- 부모 노드 인덱스 번호 = 자식 노드 인덱스 번호 / 2
- JAVA에서는 / 연산자로 몫을 구할 수 있음
- 왼쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2
- 오른쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2 + 1
- 부모 노드 인덱스 번호 = 자식 노드 인덱스 번호 / 2
힙에 데이터 삽입 구현 (Max Heap 예)
// src/com.company/Heap/Heap.java
package com.company.Heap;
import java.util.ArrayList;
public class Heap {
public ArrayList<Integer> heapArray = null;
public Heap(Integer data) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
}
}// src/com.company/Main.java
package com.company;
import com.company.Heap.Heap;
public class Main {
public static void main(String[] args) {
Heap heapTest = new Heap(1);
System.out.println(heapTest.heapArray);
}
}
// [null, 1]Heap insert 구현 1
// src/com.company/Heap/Heap.java
package com.company.Heap;
import java.util.ArrayList;
public class Heap {
public ArrayList<Integer> heapArray = null;
public Heap(Integer data) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
}
public boolean insert(Integer data) {
if(heapArray == null) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
} else {
heapArray.add(data);
}
return true;
}
}// src/com.company/Main.java
package com.company;
import com.company.Heap.Heap;
public class Main {
public static void main(String[] args) {
Heap heapTest = new Heap(1);
heapTest.insert(2);
heapTest.insert(3);
heapTest.insert(4);
heapTest.insert(5);
System.out.println(heapTest.heapArray);
}
}
// [null, 1, 2, 3, 4, 5]Heap insert 구현 2
= 삽입한 노드가 부모 노드의 값보다 클 경우, 부모 노드와 삽입한 노드 위치를 바꿈
- 삽입한 노드가 루트 노드가 되거나, 부모 노드보다 값이 작거나 같을 경우까지 반복
// src/com.company/Heap/Heap.java
package com.company.Heap;
import java.util.ArrayList;
import java.util.Collections;
public class Heap {
public ArrayList<Integer> heapArray = null;
public Heap(Integer data) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
}
// 이동할지 말지를 결정하는 함수
public boolean move_up(Integer inserted_idx) {
// 만약 최상위 노드거나 음수면 그냥 false
if(inserted_idx <= 1) {
return false;
}
Integer parent_idx = inserted_idx / 2;
if(this.heapArray.get(inserted_idx) > this.heapArray.get(parent_idx)) {
return true;
} else {
return false;
}
}
public boolean insert(Integer data) {
// parent node의 인덱스 번호와 추가 된 node의 인덱스 번호를 저장할 변수
Integer inserted_idx, parent_idx;
if(heapArray == null) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
return true;
}
// 이제 값 추가
this.heapArray.add(data);
inserted_idx = this.heapArray.size() - 1;
while(this.move_up(inserted_idx)) {
parent_idx = inserted_idx / 2;
Collections.swap(heapArray, inserted_idx, parent_idx);
inserted_idx = parent_idx;
}
return true;
}
}// src/com.company/Main.java
package com.company;
import com.company.Heap.Heap;
public class Main {
public static void main(String[] args) {
Heap heapTest = new Heap(15);
heapTest.insert(10);
heapTest.insert(8);
heapTest.insert(5);
heapTest.insert(4);
heapTest.insert(20);
// expect
// [ null, 20, 10, 15, 5, 4, 8]
System.out.println(heapTest.heapArray);
}
}
// [null, 20, 10, 15, 5, 4, 8]
Heap pop 구현 1
// src/com.company/Heap/Heap.java
package com.company.Heap;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
public class Heap {
public ArrayList<Integer> heapArray = null;
public Heap(Integer data) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
}
// 이동할지 말지를 결정하는 함수
public boolean move_up(Integer inserted_idx) {
// 만약 최상위 노드거나 음수면 그냥 false
if(inserted_idx <= 1) {
return false;
}
Integer parent_idx = inserted_idx / 2;
if(this.heapArray.get(inserted_idx) > this.heapArray.get(parent_idx)) {
return true;
} else {
return false;
}
}
public boolean move_down(Integer popped_idx) {
Integer left_child_popped_idx, right_child_popped_idx;
left_child_popped_idx = popped_idx * 2;
right_child_popped_idx = popped_idx * 2 + 1;
// CASE1: 왼쪽 자식 노드도 없을 떄 (자식 노드가 하나도 없을 떄)
if(left_child_popped_idx >= this.heapArray.size()) {
return false;
} else if(right_child_popped_idx >= this.heapArray.size()) {
// CASE2: 오른쪽 자식 노드만 없을 떄 (왼쪽 노드는 있다는 뜻)
if(this.heapArray.get(popped_idx) < this.heapArray.get(left_child_popped_idx)) {
return true;
} else {
return false;
}
} else {
// CASE3: 왼쪽/오른쪽 자식 노드가 모두 있을 떄
// 왼쪽 오른쪽 중 뭐가 더 큰지 결정 -> 왼쪽이 더 크다면
if(this.heapArray.get(left_child_popped_idx) > this.heapArray.get(right_child_popped_idx)) {
// 왼쪽이 나올 것 보다 크다면 -> 이제 바꿔야지
if(this.heapArray.get(popped_idx) < this.heapArray.get(left_child_popped_idx)) {
return true;
} else {
return false;
}
} else {
if(this.heapArray.get(popped_idx) < this.heapArray.get(right_child_popped_idx)) {
return true;
} else {
return false;
}
}
}
}
public boolean insert(Integer data) {
// parent node의 인덱스 번호와 추가 된 node의 인덱스 번호를 저장할 변수
Integer inserted_idx, parent_idx;
if(heapArray == null) {
heapArray = new ArrayList<Integer>();
heapArray.add(null);
heapArray.add(data);
return true;
}
// 이제 값 추가
this.heapArray.add(data);
inserted_idx = this.heapArray.size() - 1;
while(this.move_up(inserted_idx)) {
parent_idx = inserted_idx / 2;
Collections.swap(heapArray, inserted_idx, parent_idx);
inserted_idx = parent_idx;
}
return true;
}
public Integer pop() {
Integer returned_data, popped_idx, left_child_popped_idx, right_child_popped_idx;
// 그냥 heapArray가 null이라면 null을 반환 하는것이 맞다
if(this.heapArray == null) {
return null;
} else {
returned_data = this.heapArray.get(1);
// 이제 가장 위로 올린다
this.heapArray.set(1, this.heapArray.get(this.heapArray.size() - 1));
this.heapArray.remove(this.heapArray.size() - 1);
popped_idx = 1;
while(this.move_down(popped_idx)) {
left_child_popped_idx = popped_idx * 2;
right_child_popped_idx = popped_idx * 2 + 1;
// CASE2: 오른쪽 자식 노드만 없을 떄
if(right_child_popped_idx >= this.heapArray.size()) {
// 아래꼐 더 크면 바꾸고 이제 poped_idx를 * 2 해줘서 왼쪽 노드를 가리키게 해야 한다.
if(this.heapArray.get(popped_idx) < this.heapArray.get(left_child_popped_idx)) {
Collections.swap(this.heapArray, popped_idx, left_child_popped_idx);
popped_idx = left_child_popped_idx;
}
// CASE3: 왼쪽/오른쪽 자식 노드가 모두 있을 때
} else {
// 왼쪽이 더 크다면
if(this.heapArray.get(left_child_popped_idx) > this.heapArray.get(right_child_popped_idx)) {
// left_child_popped_idx가 더 크다면 이제 바꿔야지
if(this.heapArray.get(popped_idx) < this.heapArray.get(left_child_popped_idx)) {
Collections.swap(this.heapArray, popped_idx, left_child_popped_idx);
popped_idx = left_child_popped_idx;
}
} else {
if (this.heapArray.get(popped_idx) < this.heapArray.get(right_child_popped_idx)) {
Collections.swap(this.heapArray, popped_idx, right_child_popped_idx);
popped_idx = right_child_popped_idx;
}
}
}
}
return returned_data;
}
}
}// src/com.company/Main.java
package com.company;
import com.company.Heap.Heap;
public class Main {
public static void main(String[] args) {
Heap heapTest = new Heap(15);
heapTest.insert(10);
heapTest.insert(8);
heapTest.insert(5);
heapTest.insert(4);
heapTest.insert(20);
// expect
// [ null, 20, 10, 15, 5, 4, 8]
System.out.println(heapTest.heapArray);
heapTest.pop();
System.out.println(heapTest.heapArray);
}
}
// [null, 20, 10, 15, 5, 4, 8]
// [null, 15, 10, 8, 5, 4]
5. 힙 (Heap) 시간 복잡도
- depth (트리의 높이)를 h라고 표기한다면,
- n개의 노드를 가지는 heap에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf노드까지 비교해야 하므로 h = logn에 가까우므로, 시간복잡도는 O(log n)
'Algorithm > Algorithm-Java' 카테고리의 다른 글
| Java-알고리즘 ( bubble sort ) (0) | 2021.11.22 |
|---|---|
| Java-알고리즘 ( 공간 복잡도 ) (0) | 2021.11.22 |
| Java-자료구조 (Tree) (0) | 2021.11.19 |
| Java-자료구조 (Hash Table) (0) | 2021.11.18 |
| Java-자료구조 (시간 복잡도) (0) | 2021.11.18 |