1. 병합정렬
- 재귀용법을 활용한 정렬 알고리즘
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

2. 알고리즘 이해
- 데이터가 네 개 일떄(데이터 갯수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해 보자)
- 두 단계로 분리해서 이해할 수 있음
- 1단계: 정렬되지 않은 배열을 끝까지 분리하는 단계
- 2단계: 분리한 데이터를 단계별로 합치는 단계
- 예: dataList = [1, 9, 3, 2]
- 먼저 [1, 9], [3, 2]로 나누고
- 다시 앞 부분은 [1], [9]로 나누고 ( 여기까지 1단계 )
- 다시 정렬해서 합친다. [1, 9] ( 이 부분부터 2단계 )
- 다음 [3, 2]는 [3], [2]로 나누고
- 다시 정렬해서 합친다 [2, 3]
- 이제 [1, 9]와 [2, 3]을 합친다.
- 두 배열의 맨 앞에 위치한 데이터부터, 각각 비교하며, 정렬된 합쳐진 배열을 작성한다.
- 1 < 2이니 [1]
- 9 > 2이니 [1, 2]
- 9 > 3이니 [1, 2, 3]
- 9밖에 없으니 [1, 2, 3, 9]
- 두 배열의 맨 앞에 위치한 데이터부터, 각각 비교하며, 정렬된 합쳐진 배열을 작성한다.
3. 알고리즘의 구현
< 1 단계 >
// src/com.company/MergeSort.java package com.company; import java.util.ArrayList; public class MergeSort { public ArrayList<Integer> splitFunc(ArrayList<Integer> dataList) { // 만약 배열의 크기가 1이면 해당 값을 리턴한다. if(dataList.size() <= 1) { return dataList; } int medium = dataList.size() / 2; ArrayList<Integer> leftArr = new ArrayList<Integer>(); ArrayList<Integer> rightArr = new ArrayList<Integer>(); leftArr = this.splitFunc(new ArrayList<Integer>(dataList.subList(0, medium))); rightArr = this.splitFunc(new ArrayList<Integer>(dataList.subList(medium, dataList.size()))); return this.mergeFunc(leftArr, rightArr); } }
일단 배열을 앞뒤 두 배열로 짜르는 모드를 작성하고 이를 재귀적으로 호출하여 나중에 구현할 mergeFunc을 마지막에 반환 하도록 했습니다.
< 2 단계 >
// src/com.company/MergeSort.java package com.company; import java.util.ArrayList; public class MergeSort { public ArrayList<Integer> splitFunc(ArrayList<Integer> dataList) { // 만약 배열의 크기가 1이면 해당 값을 리턴한다. if(dataList.size() <= 1) { return dataList; } int medium = dataList.size() / 2; ArrayList<Integer> leftArr = new ArrayList<Integer>(); ArrayList<Integer> rightArr = new ArrayList<Integer>(); leftArr = this.splitFunc(new ArrayList<Integer>(dataList.subList(0, medium))); rightArr = this.splitFunc(new ArrayList<Integer>(dataList.subList(medium, dataList.size()))); return this.mergeFunc(leftArr, rightArr); } public ArrayList<Integer> mergeFunc(ArrayList<Integer> leftList, ArrayList<Integer> rightList) { ArrayList<Integer> mergedList = new ArrayList<Integer>(); int leftPoint = 0; int rightPoint = 0; // CASE1: left/right 둘 다 있을 떄 while(leftList.size() > leftPoint && rightList.size() > rightPoint) { if(leftList.get(leftPoint) > rightList.get(rightPoint)) { mergedList.add(rightList.get(rightPoint)); rightPoint += 1; } else { mergedList.add(leftList.get(leftPoint)); leftPoint += 1; } } // CASE2: right 데이터가 없을 떄 while(leftList.size() > leftPoint) { mergedList.add(leftList.get(leftPoint)); leftPoint += 1; } // CASE3: left 데이터가 없을 떄 while(rightList.size() > rightPoint) { mergedList.add(rightList.get(rightPoint)); rightPoint += 1; } return mergedList; } }
- ArrayList 만들기
- leftPoint, rightPoint = 0
- CASE1: leftList, RightList 둘 다 있을 때
- while (leftList.size() > leftPoint && rightList.size() > rightPoint)
- 만약 leftPoint 나 rightPoint 가 이미 leftList 또는 rightList 배열을 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
- if (leftList.get(leftPoint) > rightList.get(rightPoint))
- mergedList.add(rightList.get(rightPoint));
- rightPoint += 1;
- else:
- mergedList.add(leftList.get(leftPoint));
- leftPoint += 1;
- while (leftList.size() > leftPoint && rightList.size() > rightPoint)
- CASE2: RightList 만 없을 때: 나머지 LeftList 에 있는 데이터를 그대로 mergedList 뒤에 넣음
- CASE3: LeftList 만 없을 때: 나머지 RightList 에 있는 데이터를 그대로 mergedList 뒤에 넣음
이렇게 최종 완성된 코드를 돌려보면

이와같이 정렬이 완벽하게 되었음을 확인할 수 있습니다.
4. 알고리즘 분석
4. 알고리즘 분석
- 알고리즘 분석은 쉽지 않음, 이 부분은 참고로만 알아두자.
- 다음을 보고 이해해보자
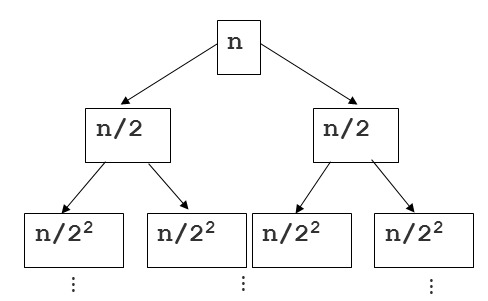
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음 그림의 예에서 는 2단계 깊이를 의미하며, 각 분리된 배열을 노드라고 부르기로 합니다.
- 각 단계에 있는 하나의 노드 안의 배열 길이는 가 된다.
- 각 단계에는 개의 노드가 있다.
- 각 단계의 각 노드 안의 배열 데이터는 한번씩은 체크되므로, 각 단계는 각각 시간 복잡도를 가짐
- 단계는 항상 개 만큼 만들어짐, 시간 복잡도는 결국 O(log n), 2는 역시 상수이므로 삭제
- 따라서, 단계별 시간 복잡도 O(n) * O(log n) = O(n log n)
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음을 보고 이해해보자
'Algorithm > Algorithm-Java' 카테고리의 다른 글
| Java - 알고리즘 ( quick sort ) (0) | 2022.03.08 |
|---|---|
| Java-알고리즘 ( Recursive, Dynamic Programming ) (0) | 2022.03.08 |
| Java-알고리즘 ( insertion sort ) (0) | 2021.11.22 |
| Java-알고리즘 ( selection sort ) (0) | 2021.11.22 |
| Java-알고리즘 ( bubble sort ) (0) | 2021.11.22 |
