[ 3D Vision - Study ] - Nerual Fields and 3D Representations

AIML/딥러닝 최신 트렌드 알고리즘

[ 3D Vision - Study ] - Nerual Fields and 3D Representations

Hyunseo😊 2024. 11. 2. 17:56

3D Vision Study의 목표는 NeRF를 한번 접해보기 위함이였습니다. NeRF는 ECCV 2020(oral)로서 best paper상을 받은 주인공이며, 그만큼 파급력이 높은 기술임을 알 수 있습니다. 당시에 최고의 complex view synthesizing 기술로서 sparse input과 continuous volumetric function을 이용했습니다. 해당 포스팅에서는 이러한 특징을 가지는 NeRF의 Concept과 Details에 대하여 살펴보겠습니다. (논문에서의 영어 표현이 더 익숙해서, 번역하지 않은 표현이 많은점 양해 부탁드립니다.)

NeRF 논문 링크: https://arxiv.org/pdf/2003.08934

Introduction

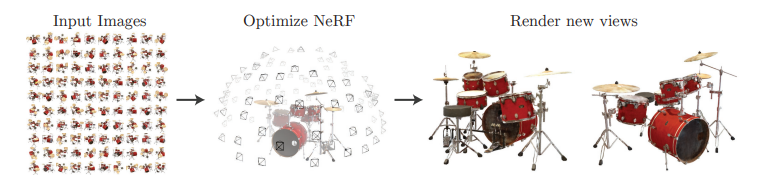
해당 논문에서는 static scene(각각의 이미지)를 5D function으로 각각의 방향 정보인 \((\theta, \phi)\)와 위치 정보인 \((x, y, z)\)로 표현합니다. 그리고 density라는 개념도 등장하는데, 이는 특정 위치에서 ray(광선)이 얼마나 많이 흡수되거나 산란되는지를 나타내는 값입니다. NeRF는 ray를 따라 여러 지점의 색상과 density를 합성하여 최종 픽셀 색상을 계산합니다. density가 높을수록 해당 지점이 최종 색상에 큰 영향을 미치게 되는 것입니다.

NeRF는 deep fully-connected(MLP) 네트워크만을 사용하여 \((x, y, z, \theta, \phi)\)를 input으로 넣어, volumn density와 view dependent한 RGB color를 얻습니다. NerF의 동작 순서를 정리하면 아래와 같습니다.

camera의 ray를 3D scene으로 marching(접근)시켜 3D의 sampled set을 생성합니다.
위에서 생성한 set을 이용하여 MLP에 넣어 output으로서, colors와 densities를 구합니다.
volume rendering을 통해 colors와 densities를 하나의 2D image로 accumulate합니다.

volume rendering은 미분가능하므로, 우리의 최적화 목표는 GT와 MLP의 결과로서 redering된 2D image의 loss를 최소화하게 학습해나가면 됩니다. 디테일한 부분에 대해 간단히 짚고 가자면, NeRF에서는 position encoding을 통해 MLP가 higher frequency functions의 표현을 가능하게함으로써 해결합니다. 또한, high frequency function을 표현하는데 필요한 query를 확보하기 위해 hierarchical sampling(계층 샘플링)을 활용합니다. 최종적으로 NeRF는 high resolution의 복잡한 장면을 modeling할때 discretized voxel grids방법에서 발생하는 엄청난 storage문제를 해결합니다.

Nerual Randiance Field Scene Representation

입력이 위치 \(x = (x, y, z)\)와 2D 시점 방향인 \((\theta, \phi)\)이고, 출력이 color \(c = (r, g, b)\)와 density \(\sigma\)인 5D vector값 함수로 연속장면을 만들어 낼 수 있습니다. 논문에서 방향을 3D Cartesian unit vector d로 표현합니다. NeRF는 MLP를 이용하여 \(F_{theta} : (x, d) \rightarrow (c, \sigma)\)를 사용하여 연속적인 5D 장면 표현을 근사화하고 가중치 \(\theta\)를 최적화하여 5D 좌표상에서의 volum density와 directional emitted color로 매핑됩니다.

저자들은 volum density \(\sigma\)를 위치 \(x\)의 함수로 예측하도록 제한합니다. 이는 density값이 특정 위치에서의 고유한 물리적 특성을 나타내게 하여, multi view consistency를 보장하기 위함입니다. 뒤에서도 언급하겠지만 \((\theta, \phi)\)는 extrinsic parameters인 C2W(Camera to World) matrix를 만들 때 이용이 되고, C2W matrix를 통해서 만들어진 \((x, y)\)의 Ray와 Ray 위에서 sampling되는 \(z\)가 model로 들어가는 것입니다. 이 말은, 모델의 처음 들어가는 input은 direction 정보가 빠진 \((x, y, z)\)인 것입니다. NeRF에서 모델 중간에 Ray의 direction정보를 넣어주어 RGB 색상 c가 location, direction모두의 함수로 예측되도록 하여 표현됩니다. 아래는 공식 github에서 코드를 가져왔습니다.

# Ray helpers
def get_rays(H, W, K, c2w):
    i, j = torch.meshgrid(torch.linspace(0, W-1, W), torch.linspace(0, H-1, H))  # pytorch's meshgrid has indexing='ij'
    i = i.t()
    j = j.t()
    dirs = torch.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -torch.ones_like(i)], -1)
    # Rotate ray directions from camera frame to the world frame
    rays_d = torch.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1)  # dot product, equals to: [c2w.dot(dir) for dir in dirs]
    # Translate camera frame's origin to the world frame. It is the origin of all rays.
    rays_o = c2w[:3,-1].expand(rays_d.shape)
    return rays_o, rays_d

이를 위해 MLP \(F_{theta}\)는 먼저 8개의 fully-connected layer(ReLU 함수와 layer당 256개의 channel)로 3D 좌표 \((x, y, z)\)를 처리해 \(\sigma\)와 256d의 feature vector를 출력합니다. feature vector는 Ray의 viewing direction과 concatenate되어 view에 따른 RGB색상을 출력하는 또다른 fully-connected layer(ReLU 함수와 layer당 126개의 channel)로 전달됩니다.

non-Lambertian effects란 표면이 빛을 균일하게 반사하지 않는 현상을 의미합니다. non-Lambertian효과는 현실감 있는 렌더링에 필수적입니다. NeRF는 신경망을 통해 각 지점의 색상을 방향에 따라 달리 예측함으로써 non-Lambertian효과를 정확히 모델링할 수 있습니다.

위 그림에서 볼 수 있듯이 view 의존성 없이 학습된 모델은 3번째 그림과 같이 반사를 표현하는데 어려움이 있습니다.

Volume Rendering with Randiance Fields

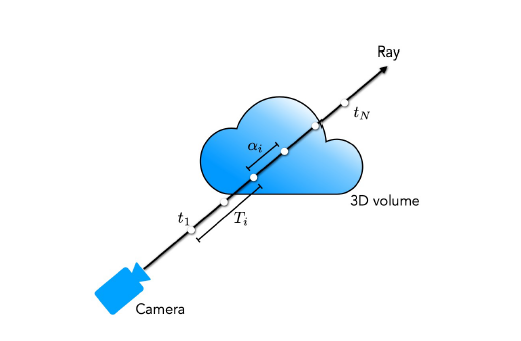
NeRF에서 5D NeRF 표현은 3D 공간의 모든 지점에서 density와 color로 장면을 나타냅니다. 저자들은 고전적인 volume rendering를 사용하여 redering하고자 하는 장면을 통과하는 모든 Ray의 색상을 rendering합니다. 밀도 \(\sigma(x)\)는 Ray가 위치 x의 무한히 작은 입자(국소입자)에서 끝나는 미분가능한 확률로 해석될 수 있습니다. near bound \(t_n\)과, far bound \(t_f\)의 Ray \(r(t) = o + td\)의 predicted color \(C(r)\)는 아래와 같이 표현될 수 있습니다.

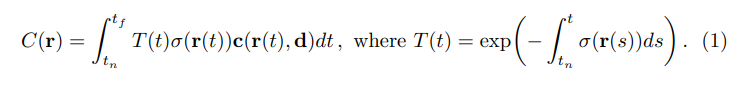
위 수식에서 \(T(t)\)는 \(t_n ~ t\)까지의 accumulated transmittance(누적 투과율), 즉 Ray가 다른 입자에 부딪히지 않고 \(t_n ~ t\)로 이동할 확률을 나타냅니다. 연속적인 neural field에서 view를 redering하려면 rendering하고자 하는 가상의 카메라의 각 픽셀로부터 추적되는 Ray에 대해 \(C(r)\)을 추정하면 됩니다.

quadrature estimation(구적법)을 사용하여 \(C(r)\)의 연속적인 적분을 numerical하게 구합니다. 일반적으로 이는 이산화된 voxel grids를 rendering하는 데 사용되는데, MLP가 고정된 이산 위치 집합에서만 쿼리되기 때문에 표현의 해상도가 효과적으로 제한됩니다. 대신, 저자들은 N개의 균일한 간격의 bin\([t_n, t_f]\) 와 같이 분할하여 각 bin 내에서 하나의 샘플을 균일한 확률로 추출하는 stratified sampling을 사용합니다.

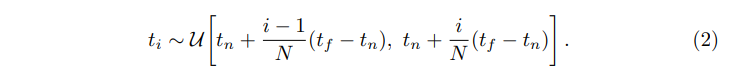
여기서 적분값을 추정하기 위해 sample들의 이산적인 집합을 사용하지만, stratified sampling을 사용하면 최적화 단계에서 MLP가 평가되면서 연속적인 장면 표현을 나타낼 수 있습니다. 위와같은 sample들을 사용하여 아래와같이 \(C(r)\)을 추정합니다.

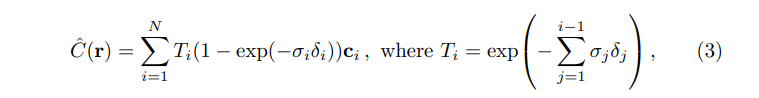
\(\delta_i = t_{i+1} - t_i\)는 인접 샘플 사이의 거리입니다. \((c_i, \sigma_i\)의 집합에서 \(\hat{C}(r)\)를 계산하기 위한 위 함수는 간단히 미분 가능하며 \(\alpha_i = 1 - exp(-\sigma_{i}\delta_{i})\)는 view rendering부분에서 사용되는 전통적인 알파 합성입니다. (알파합성은 color와 density를 합성하는 고전적인 방법입니다)

Optimizing a Neural Randiance Field

위에서 NeRF는 고해상도의 복잡한 장면을 rendering하여 SOTA결과를 낼 수 있도록 했던 몇가지 개선사항에 대해 간단히 언급만 했습니다. 그 중 첫번째는 MLP가 고주파 함수를 잘 표현할 수 있도록 하는 input 좌표에 대한 positional encoding이고, 고주파 표현을 효율적으로 샘플링할 수 있는 hierarchical sampling(계층적 샘플링) 절차 입니다.

1. Positional Encoding

Universal Function approximators(보편 근사이론)에도 불구하고, 저자들은 \(F_{\theta}\)를 \(xyz\theta\phi\) input을 이용해서 연산하도록 하면 색상과 형상의 고주파 변화를 나타내는데 한계가 있음을 발견합니다. 신경망이 저주파 함수를 학습하는 쪽으로 편향되어 있음을 보여줍니다. 추가적으로 저자들은 고주파 함수를 이용해 input을 MLP에 넣기 전에 높은 차원에 mapping시켜주면 고주파 변화가 포함된 포함된 데이터의 피팅에 이점이 있음을 보입니다.

저자들은 이러한 발견을 활용하고 \(F_{\theta}\)를 두개의 함수인 \(F_{\theta}^{'}\circ \gamma\)(하나는 학습, 하나는 학습시키지 않음)으로 재구성하면 성능을 크게 증가시킬 수 있음을 보입니다. 아래 4번째 그림을 보면, Potional Encoding을 사용하지 않으면 고주파 변화를 MLP가 잘 학습하지 못함을 볼 수 있습니다.

논문에서 \( \gamma \)는 \(\mathbb{R}\)에서 \(\mathbb{R}^{2L}\)로의 매핑이고, \(F_{\theta}^{'}\)는 우리가 아는 단순 MLP입니다. 논문에서 소개하는 encoding function은 아래와 같습니다.

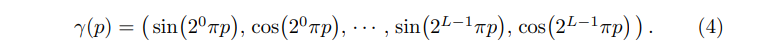
\(\gamma(\cdot)\)는 \([-1, 1]\)로 정규화된 \(x\) 각각의 값과 Cartesian norm vector인 \(d\)의 세 성분에 각각 적용됩니다. 저자들은 \(\gamma (x)\)에 대해 \(\mathsf{L} = 10\), \(\gamma (d)\)에 대해 \(\mathsf{L} = 4\)로 설정합니다.

이러한 positional encoding은 Transformer 구조에서도 사용되는데, 이는 순서 개념이 포함되지 않은 아키텍처에 대한 입력으로 sequence에서 이산적인 위치를 제공하기 위함으로서 사용됩니다. NeRF에서는 positional encoding을 연속적인 입력 좌표를 더 높은 차원으로 mapping하여 MLP가 더 높은 주파수의 변화에도 피팅이 되도록 하는데에 차이점이 있습니다.

2. Hierarchical volume sampling

Eqns. 2, 3에서 봤던 수식처럼 각 카메라 Ray를 따라 N개의 쿼리 지점에서 NeRF를 평가하는 방법은 비효율적입니다. 이러한 방법은, 렌더링된 이미지에 기여하지 않는 free-space, occluded space가 반복적으로 샘플링되기 때문입니다. 저자들은 volume-rendering의 초기 방법에 영감을 받아 최종 렌더링의 예상 효과에 비례한 샘플을 할당한 계층적 샘플링을 제안합니다.

NeRF에서는 이를 위해 하나의 신경망을 사용하는 대신 "coarse"와 "fine"네트워크 두 개를 동시에 학습합니다. 먼저 stratified sampling을 통해 \(N_c\)개의 3D 위치를 샘플링하여 네트워크를 평가합니다. 이 coarse 네트워크의 출력을 바탕으로 물체의 volume과 관련된 부분을 샘플링할 수 있도록 편향 sampling합니다. 이를 위해 먼저 아래와 같이 coarse 네트워크 \(\hat{C}_{c}(r)\)의 식을 ray에서 샘플된 \(c_i\)의 가중합 형태로 표현해줍니다.

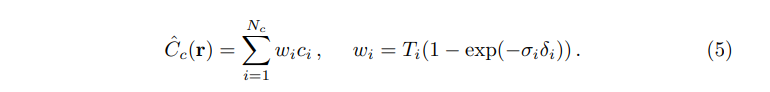
위에서 다시쓴 가중합 \(w_i\)을 \(\hat{w}_i \ w_i / \sum^{N_c}_{j=1}w_j\)의 형태로 정규화하여 picewise-constant PDF를 만듭니다. 위 PDF를 또다시 inverse transform sampling(역변환 샘플링)을 하여 해당 분포에서 \(N_f\)를 sampling하고, 첫번째 샘플의 집합과의 합집합을 하여 fine 네트워크를 평가하여 \(\hat{C}_{f}(r)\)를 계산하여 Ray의 최종 렌더링된 색상을 구합니다.

이는 각 샘플을 적분의 독립적인 확률추정으로 처리하는 대신, 샘플링된 값을 적분 전체 영역의 nonuniform discretization으로 사용하여 volume이 포함될 것으로 예상되는 영역에 더 많은 샘플을 할당한다고 보면 됩니다.

3. Implementation details

NeRF는 각 장면에 대해 연속적인 volume rendering network를 최적화 합니다. 이를 위해서는 장면의 캡쳐된 GT, 카매라 pose, intrinsic parameter, 장면 경계로 구성된 데이터셋이 필요합니다(COLMAP 활용하여 수집). 각 최적화 단계에서 모든 픽셀 집합에서 camera ray의 batch를 샘플링 한 다음, Coarse 네트워크로부터 계층적 샘플링을 통해 \(N_c\)개의 샘플을 query하고, 이를 통해 fine 네트워크의 \(N_c + N_f\)개의 샘플을 query합니다. 그 후, volume rendering을 통해 두 샘플 집합 모두에서 Ray의 색상을 rendering합니다. Loss는 아래와 같이 coarse, fine 렌더링과 GT에 대한 MSE로서 표현됩니다.

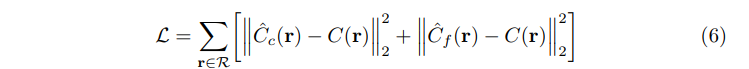
\(\mathcal{R}\)은 batch의 Ray집합이고, \(C(r)\)은 GT의 RGB, \(\hat{C}_{c}(r)\)은 coarse 네트워크의 렌더링, \(\hat{C}_{f}(r)\)는 fine 네트워크의 렌더링 RGB가 됩니다. 최종 렌더링은 \(\hat{C}_{f}(r)\)를 통해 진행되지만, \(\hat{C}_{c}(r)\)의 loss도 포함하여 최소화함으로써, coarse 네트워크의 가중치 분포를 fine 네트워크에 샘플을 할당할 수 있습니다.

실험에서는 4096개의 ray 집합으로 이루어진 batch를 사용했고, \(N_c = 64, N_f = 128\)를 사용합니다. Adam Optimizer, learning rate를 \(5x10^{-4}\)와 decay 값을 \(5x10^{-5}\)를 최적화 단계에 사용합니다. 이를 통해 NVIDIA V100 GPU를 사용하여 한 장면당 100-300K개의 iteration을 수렴할때까지 대략 1-2일 진행 하였다고 합니다.

NeRF논문에서 말하는 training set은 특정 장면에 대해 학습을 진행할 때 사용하는 여러 시점에서 촬영된 이미지 집합을 의미합니다. 즉, 하나의 장면을 학습하기 위해 다양한 각도에서 촬영된 이미지들이 training set으로 사용되는 것입니다. NeRF에서 새로운 시점에서의 렌더링 품질을 평가하기 위해 일부 이미지는 test set으로 분리되기도 합니다.

또한, NeRF는 새로운 장면이 주어질 때마다 그 장면에 대해 학습을 진행하고, 학습된 모델을 통해 테스트 시 다양한 시점의 이미지를 생성하는 방식입니다. 즉, 사전에 일반화된 모델을 학습해 두는 것이 아니라, 특정 장면에 특화된 신경망을 학습하는 개념입니다.

Results

1. Datasets

NeRF 모델의 성능을 평가하기 위해 아래와 같은 데이터셋을 사용합니다.

Diffuse Synthetic 360˚ (DeepVoxels 데이터셋)
- 내용: 단순한 기하학적 형태를 가지며, 람베르트 반사(Lambertian)를 따르는 4개의 물체로 구성됩니다.
- 이미지 해상도: 각 이미지의 해상도는 512 x 512 픽셀입니다.
- 시점: 물체들은 상부 반구(upper hemisphere)에서 촬영한 여러 시점에서 렌더링됩니다.
  - 학습용 이미지: 479장
  - 테스트용 이미지: 1000장
Realistic Synthetic 360˚ (자체 생성 데이터셋)
- 내용: 복잡한 기하학적 구조와 비-람베르트 반사(non-Lambertian) 특성을 가진 8개의 물체로 구성됩니다.
- 이미지 해상도: 각 이미지의 해상도는 800 x 800 픽셀입니다.
- 시점:
  - 6개의 물체는 상부 반구(upper hemisphere)에서 촬영한 시점에서 렌더링됩니다.
  - 2개의 물체는 전체 구(sphere)에서 촬영한 시점에서 렌더링됩니다.
- 학습용 이미지: 각 장면당 100장
- 테스트용 이미지: 각 장면당 200장

2. Comparisons

위 표에 등장하는 LLFF 데이터셋은 다양한 실제 장면을 촬영한 멀티뷰 이미지 데이터셋으로서, 전방을 바라보는 시점(Forward-facing views)에서 장면을 촬영하여, 현실적인 환경에서의 3D 구조를 복원하는데 사용됩니다. LLFF방법론은 다수의 이미지 시점(localized light field)을 결합하여 장면을 복원하는 기법중에 하나입니다.

위 표의 평가지표는 PSNR(신호 대 잡음비)와 SSIM(구조적 유사도)로 높을수록 좋은 결과를 의미하며, LPIPS(지각적 유사도)는 낮을수록 좋은 결과를 의미합니다. 또한, NV(New View Synthesis)는 LLFF에 대해서는 평가되지 않았는데, NV는 장면 경계를 벗어난 물체까지 복원하지 못하기 때문입니다.

결과를 보면, NeRF의 방법이 PSNR, SSIM 면에서 기존 방법인 SRN, NV, LLFF를 능가합니다. LLFF가 LPIPS에서 약간 더 나은 결과를 보였지만, NeRF는 더 나은 멀티뷰 일관성을 달성했고, 시작적 오류(artifact)가 적게 발생했습니다.

위 그림은 new synthetic dataset의 test-set view에서의 대해 NeRF와 LLFF, SRN, NV를 통해 렌더링 결과를 qualitatively하게 비교한 결과입니다. NeRF가 다른 방법에 비해 non-Lambertian 반사나, artifacts, ghost등이 나타나재 않고 정교하게 GT와 비슷한 것을 볼 수 있습니다.

이는 real world scene에 대한 결과입니다.

3. Disccusion

저자들은 NeRF는 SRN, NV, LLFF와 비교해 더 높은 품질의 시점 합성을 제공하며, LLFF 대비 매우 적은 메모리로 장면을 표현할 수 있다고 합니다. SRN과 NV는 해상도 및 표현력 한계가 있고, LLFF는 시차가 큰 데이터셋에서 형상을 정확하게 추정하지 못하는 문제점을 가진다고 합니다.

4. Ablation studies

Row 1은 가장 미니멀한 버전입니다. Row 2~4는 PE(Positional-Encoding), VD(View-Dependence), H(Hierarchical sampling)중 하나씩을 Ablation한 결과입니다. Row 2~4에서 알 수 있는 점은, PE, VD가 H보다 quantitative benefit을 더 가져다 준다는 점입니다. Row 5~6은 input image를 줄이면 어떨까에 대한 결과입니다. 저자들은 오직 25개의 input image(train-set)만으로 NV, SRN을 모든 메트릭에서 높고, 100개의 이미지로 LLFF과 모든 메트릭에 대해 견줄 수 있다고 합니다. Row 7~8은 maximum frequencies를 조절합니다. \(mathcal{L} = 5, 15\)은 positional encoding에 사용되는 \(x\)에 대한 값이고, \(d\)에 대한 값은 proportinally하게 scale해주었다고 합니다. 저자들은 \(mathcal{L}\)을 10에서 15로 갈때 어떠한 성능향상도 없었다고 하는데, 저자들은 \(mathcal{L}\)은 \(2^{mathcal{L}}\)이 샘플된 이미지 개수보다 크면 영향이 거의 없을 것이라고 합니다.

Concluison

NeRF가 discretized voxel representation을 output으로하는 convolution network을 보충하여 더 좋은 결과를 낼 수 있었다고 합니다. 저자들은 계층적 샘플링 전략을 통해 효율성을 높일려고 했지만, 여전히 Neural Randiance Field를 더 효율적으로 최적화하고 렌더링하기 위한 추가 연구의 필요성이 여전히 존재한다고 지적합니다. 또한, interpretability(해석 가능성)도 중요한 미래 연구 방향으로 제안합니다. Voxel grid나 meshes와 같은 샘플링 표현 방식은 렌더링 품질이나 오류를 예측하고 분석하는데 유용합니다. 반면, 신경망 가중치에 장면을 인코딩하는 방식은 이러한 해석이 어려워 NeRF의 실패 요인(failure point)이나 렌더링 품질을 분석하기 위한 방법론이 부족하다고 합니다.

E. NDC ray space derivation

NDC(Normalized Device Coordinate)는 공간 스펙트럼에 대한 모양을 normalize시켜주는 것입니다. NDC는 NeRF에서 장면의 특정 카메라 설정과 장면 범위에 맞춰 좌표를 정규화하여 효율적으로 학습하기 위해 사용하는 좌표계입니다. 이는 특히, llff와 같이 forward-facing(전방을 바라보는)장면을 렌더링할 때 사용됩니다.

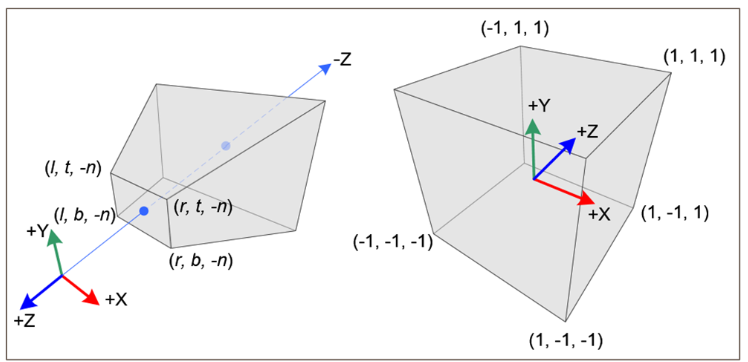
https://velog.io/@gjghks950/NeRF-Representing-Scenes-as-Neural-Radiance-Fields-for-View-Synthesis-%ED%86%BA%EC%95%84%EB%B3%B4%EA%B8%B0

NeRF의미지는, COP(카메라)에서 World를 관찰하는 unbounded frustrum형태입니다. NeRF는 input으로 3D 위치를 사용하기 때문에, 공간 전체를 효율적으로 표현할 방법이 필요합니다. 그렇기 때문에 ubounded frustrum형태로 관찰한 real world를 \([-1, 1]\)범위의 Normalized Device Coordinate(NDC)로 바꿔주어야 하는 것입니다. 일반적인 NDC의 방법은, unnormalized real world coordinates(near, far로 제한)을 NDC로 mapping하는 projection matrix를 구해야 합니다. 이에 대한 방법은 위 링크의 블로그에서 따왔습니다.

구해진 \(M\)행렬을 사용하여 카메라 좌표계에서 얻은 3D 좌표를 NDC좌표료 변환합니다. 이를 통해 NDC 공간으로 변환된 좌표를 사용하면 Ray의 샘플링과 깊이 분포를 일정하게 유지할 수 있게됩니다. 예를 들어 원근법에 의한 왜곡이 줄어들어, 멀리 있는 물체에 대하여도 일관되게 샘플링할 수 있게됩니다. 뿐만 아니라, 불필요한 계산을 줄이고 메모리 사용을 최적화할 수 있습니다.

저작자표시 동일조건