[ 3D vision - Study ] - Point Cloud Networks (Finding Good Correspondeces) - 2
Graph convolutional networks

실제로 Graph의 가중치를 업데이트 하는 수식은 위와 같습니다. 여기서 t는 정보가 얼마나 흘렀냐에 대한 지표입니다. 아무런 정보도 주어지지 않았을때 어떻게 업데이트 되는지를 \(W_0^t\)라고 하고, 다른 vertex로부터 정보를 \(W_1^t\)라고 한다면 위와 같이 업데이트를 할 수 있습니다.
이러한 수식은 그냥 나온 수식이 절대 아닙니다. 뒤에 복잡한 motivation이 존재합니다. 이름또한 Graph convolution인 이유도 여기에 있습니다. 이에 대한 수학적인 유도를 아주 간단히만 살펴보겠습니다. 결론만 살짝 말하자면, Fourier space(graph Laplacian을 사용)에서 graph multiplcation을 하면, convolution연산에 대한 식이 나옵니다.
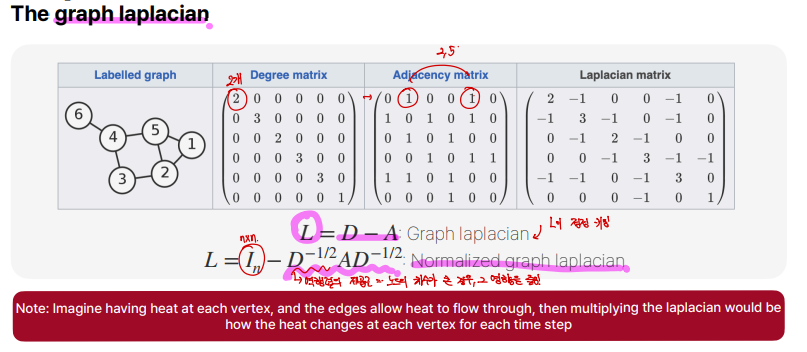
graph laplacian은 graph를 matrix로 표현했을때 나오는 attribute중에 하나입니다. Degree matrix - Adjacency matrix를 하게되면 Laplacian matrix(=\(L\))가 나오게 됩니다. 여기서 \(L\) matrix를 계속 곱하게 되면, element가 무한으로 커지게 됩니다. 그래서 normalized graph laplacian을 만들게 되는데, 이는 \(L = I_n - D^{-1/2}AD^{-1/2}\)와같이 표현됩니다. 여기서 \(D^{-1/2}\)는 역행렬의 제곱근으로써, node의 차수가 큰 경우, 이에 대한 영향을 줄이는 것이라고 생각하면 됩니다.

\(L_{norm}\) matrix는 real symmetric positive semidefinite matrix입니다. 이러한 성질 덕분에, \(L = U \wedge U^T\)와 같이 표현가능합니다(=Spectral Decomposition). 이 분해는 라플라시안의 고유값 및 고유벡터를 이용한 대각화(diagonalization)과정입니다. 여기서 \(U\)는 orthonormal matrix입니다. \(L_{norm}\)의 고유벡터들로 이루어져 있으며, 이들은 graph의 푸리에 기저(Fourier basis)로 간주합니다. \( \wedge \)는 고유값을 대각 성분으로 가지는 대각 행렬(diagonal matrix)입니다. \(L_{norm}\)의 고유값을 포함하며, 이 고유값들은 그래프의 주파수 성분을 나타냅니다. 사실 이미지에서 푸리에 변환한다, 신호 푸리에 변환한다 하는 것들은 디지털화된 matrix로 신호를 생각하게 되면 이러한 선형변환에 불과하다는 것을 알 수 있습니다.

맨 위에 convolution식이 있습니다. 푸리에 변환을 signal x, y에 대해 하고 element wise하게 곱한다음에 결과를 푸리에 변환하는 것이 convolution입니다. 이를 통해 식을 정리해보겠습니다. \[g_{\theta}(L)x = g_{\theta}(U \wedge U^T)x = Ug_{\theta}U^{T}x\]. 위 식에서 필터는 eigen value(주파수)에만 적용되므로 이렇게 정리할 수 있게됩니다.
우리는 이를 다시 convolution식과 matching시켜볼 수 있는데, \(g_{\theta}\)가 \(U^{T}y\)가 됩니다. 결국 \(L\) matrix를 곱하게 되면 convolution을 한 것과 같은 효과가 난다라는게 이 수식이 시사하는 바 입니다.

\(g_{\theta}( \wedge )\)를 근사하고 변수를 특수하게 설정하면, 위와같이 근사할 수 있습니다. 맨 아래에 네모를 친 식은 우리가 처음에 얘기한 graph convolution이라고 명명하는 식과 비슷한 꼴임을 볼 수 있습니다.
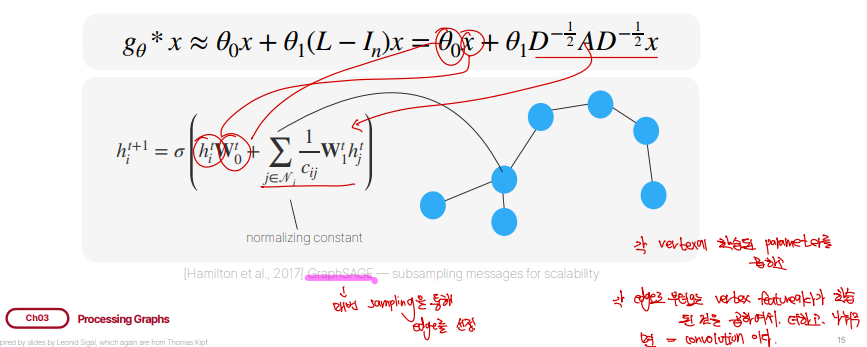
결론은 이와 같습니다. 각 vectex에다가 학습된 파라미터들을 곱하고, 또 각 다른 엣지로부터 오는 다른 vertex feature에다 학습된 걸 곱해서 더하는데, 값이 폭발하지 않게 normalization까지 해주면 이는 convolution과 다름이 없다는 것입니다. 해당 방법에서 connect되어있는 모든 node(\(N_i\))를 고려하는데, 만약 매우 많은 vertex와 연결되어있다면 문제가 되게 돼서, 매번 sampling을 통해 일부 edge만 뽑아서 더해나가는 방식으로 convolution을 진행하는 방식을 제안한 GraphSAGE도 있습니다.

2018년에는, vertex간의 중요한 연결을 스스로 학습하기 위해 attention(\(\alpha_{ij}\))을 사용하여 구현하기도 했습니다. 이를 위해서는 위 식에서 새로운 파라미터들이 필요한 것을 볼 수 있습니다.

실제로 Inductive방식의 실험에서 GraphSAGE보다 GAT(attention 기반)이 훨씬 PPI(성능)이 높은것을 볼 수 있습니다. 참고로 transductive는 학습 과정에서 모르는 정보를 유추하여 진행하는 task를 말합니다. 3d vision에서는 주로 inductive task만 사용됩니다.
Dynamic Graph CNN (EdgeConv) [Wang et al., 2019]
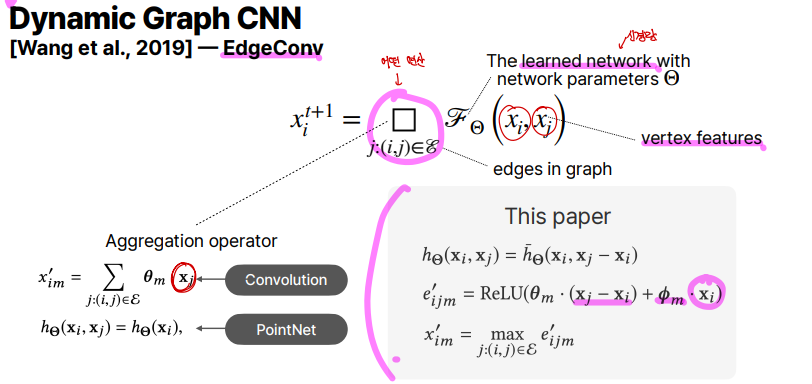
위 수식을 보면, 기존 \(F_\theta (x_i, x_j)\)는 learned network입니다. 하지만 그 앞에 네모는 Aggregation operator라고 하는데, parametric일수도 있고 그냥 수식일 수도 있습니다. convolution, pointNet연산 모두다 가능합니다. 하지만 논문에서 제안하는 Aggregation operator는 \(x_j - x_i, x_i\)에 각각 다른 parameterize된 matrix를 곱하고 ReLU를 씌운 후, max연산을 취하여서 가장 큰 값을 가지는 주변의 edge \(j\)를 구합니다.
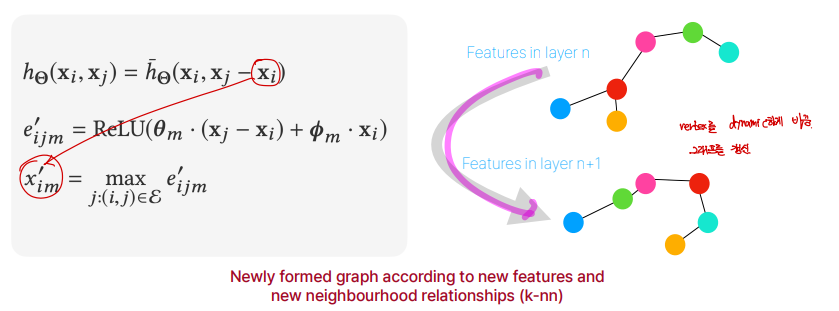
DGCNN에서 특별한점은, Dynamic하다는 것입니다. input feature가 \(x_{im}^i\)로 변환되게 되면, 최종적으로 feature space에서 가까운 점들과 멀어진 점들이 바뀌게 될 것입니다.
이와같이 dynamic하게 그래프를 변형한다는 것은, 고정된 공간적 연결이 아니라, 각 레이어에서 점들의 특징 값에 따라 그래프의 연결을 조정한다는 것을 의미합니다. 이렇게하면, 고정된 인접성에 의존하지 않아 더 유사한 점들끼리 연결하게 하며 점들의 유사성을 반영하여 학습된 특징들 간의 유사성이 더 중요한 기준이 되어, 이웃 관계가 형성됩니다.
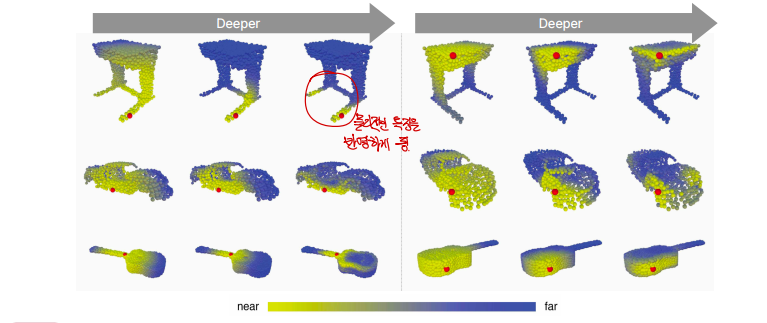
위 실험 결과는 위에서 말한 EdgeConv의 특성을 뒷받침합니다. 처음에는 빨간 점으로부터 물리적인 거리가 멀어지면 이의 값은 흐려집니다(파란색, 멀어짐). 점차 포인트들이 처리되기 시작하면 가까운 포인트들의 정의가 점점 바뀌게 됩니다. 정말 물리적인 의미를 추출해서 비슷한것끼리 가깝게 feature space를 유지시키는 것을 볼 수 있습니다.
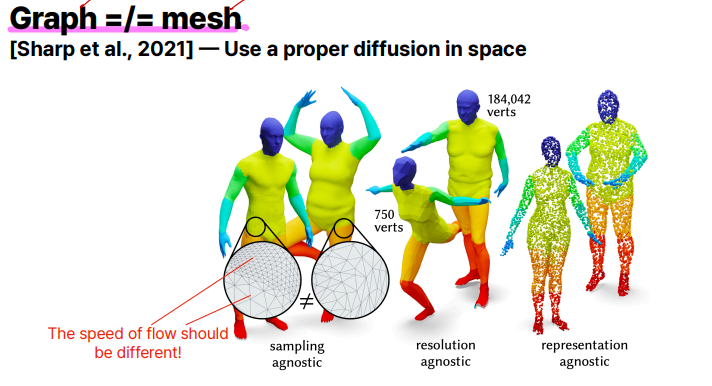
Graph neural network를 사용하는 라플라시안 같은 경우는 단순히 vertex의 얼마만큼의 엣지가 많이 연결되어 있는가를 표기하지, 물리적으로 vertex가 얼마나 많이 떨어져 있는가는 고려하지 않습니다. 반면 mesh를 처리하는 경우 멀리 떨어져있는 vertex인 경우 영향을 천천히 받아야 하는데, 기본적인 Graph neural network를 사용할때에는 고려되지 않습니다. 이러한 물리적인 의미가 들어가게끔 하는 연구가 Diffusion을 활용하여 진행되고 있습니다.
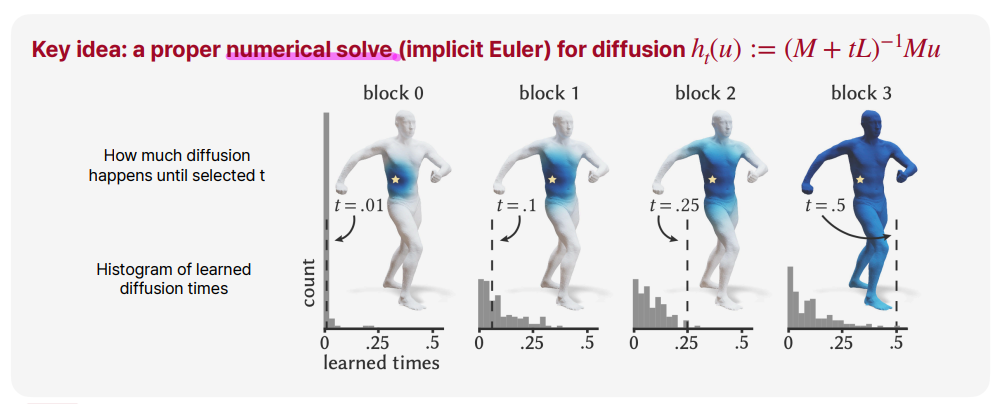
이와같이 numerical PDE solver를 이용하여 해결하게되면, 위와같은 문제점을 해결할 수 있게됩니다.